Отношение порядка. Упорядоченные множества

Отношение эквивалентности. Связь отношения эквивалентности с разбиением множества на классы

Определение. Отношение R на множестве Х называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Пример. Рассмотрим отношение «х однокурсник у» на множестве студентов педфака. Оно обладает свойствами:

1) рефлексивности, т.к. каждый студент является однокурсником самому себе;

2) симметричности, т.к. если студент х является однокурсником студента у, то и студент у является однокурсником студента х;

3) транзитивности, т.к. если студент х - однокурсник у, а студент у – однокурсник z, то студент х будет однокурсником студента z.

Таким образом, данное отношение обладает свойствами рефлексивности, симметричности и транзитивности, а значит, является отношением эквивалентности. При этом множество студентов педфака можно разбить на подмножества, состоящие из студентов, обучающихся на одном курсе. Получаем 5 подмножеств.

Отношением эквивалентности являются также, например, отношение параллельности прямых, отношение равенства фигур. Каждое такое отношение связано с разбиением множества на классы.

Теорема. Если на множестве Х задано отношение эквивалентности, то оно разбивает это множество на попарно непересекающиеся подмножества (классы эквивалентности).

Верно и обратное утверждение: если какое-либо отношение, заданное на множестве Х, порождает разбиение этого множества на классы, то оно является отношением эквивалентности.

Пример. На множестве Х = {1; 2; 3; 4; 5; 6; 7; 8} задано отношение «иметь один и тот же остаток при делении на 3». Является ли оно отношением эквивалентности?

Построим граф данного отношения: (самостоятельно)

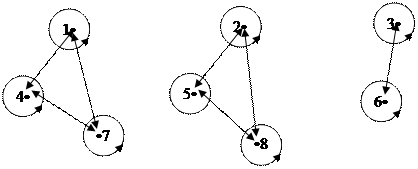Данное отношение обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, является отношение эквивалентности и разбивает множество Х на классыэквивалентности. В каждом классе эквивалентности будут числа, которые при делении на 3 дают один и тот же остаток: Х ₁ = {3; 6}, Х ₂ = {1; 4; 7}, Х ₃ = {2; 5; 8}.

Считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом этого класса. Так, класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу.

В начальном курсе математики также встречаются отношения эквивалентности, например, «выражения х и у имеют одинаковые числовые значения», «фигура х равна фигуре у».

Определение. Отношение R на множестве Х называется отношением порядка, если оно транзитивно и асимметрично или антисимметрично.

Определение. Отношение R на множестве Х называется отношением строгого порядка, если оно транзитивно и асимметрично.

Примеры отношений строгого порядка: «больше» на множестве натуральных чисел, «выше» на множестве людей и др.

Определение. Отношение R на множестве Х называется отношением нестрогого порядка, если оно транзитивно и антисимметрично.

Примеры отношений нестрогого порядка: «не больше» на множестве действительных чисел, «быть делителем» на множестве натуральных чисел и др.

Определение. Множество Х называют упорядоченным, если на нем задано отношение порядка.

Пример. На множестве Х = {1; 2; 3; 4; 5} заданы два отношения: «х £ у» и «х – делитель у».

Оба эти отношения обладают свойствами рефлексивности, антисимметричности и транзитивности (постройте графы и проверьте свойства самостоятельно), т.е. являются отношением нестрогого порядка. Но первое отношение обладает свойством связности, а второе – нет.

Определение. Отношение порядка R на множестве Х называется отношением линейного порядка, если оно обладает свойством связности.

В начальной школе изучаются многие отношения порядка. Уже в первом классе водятся отношение «меньше», «больше» на множестве натуральных чисел, «короче», «длиннее» на множестве отрезков и др.

Контрольные вопросы

1. Дайте определение бинарного отношения на множестве Х.

2. Как записать утверждение о том, что элементы х и у находятся в отношении R?

3. Перечислите способы задания отношений.

4. Сформулируйте свойства, которыми могут обладать отношения. Как данные свойства отражаются на графе?

5. Какими свойствами должно обладать отношение, чтобы оно являлось отношением эквивалентности?

6. Как отношение эквивалентности связано с разбиением множества на классы?

7. Какими свойствами должно обладать отношение, чтобы оно являлось отношением порядка?

Дата добавления: 2013-12-12