КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Транзитивность
Связность (полнота).
Асимметричность.
Антисимметричность.
Антирефлексивность.
Отношение называется антирефлексивным, если для всех x выполняется условие: ùxjx (символ “ ù“ означает “не выполняется”) или 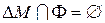 .
.
3. Симметричность.
Отношение называется симметричным, если для всех x выполняется условие: xjy Þ yjx или Ф=Ф-1.
Отношение называется антисимметричным, если для всех x выполняется условие: xjy и x¹y Þù yjx или 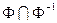 ÍDM.
ÍDM.
Отношение называется асимметричным, если для всех x выполняется условие: xjy Þù yjx или 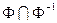 =Æ.
=Æ.
Отношение называется связным (полным), если для всех x выполняется условие: x¹y Þ xjy или yjx или М2DMÍ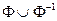 .
.
Отношение называется транзитивным, если для всех x выполняется условие: xjy и yjz Þ xjz или Ф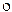 ФÍФ.
ФÍФ.
ПРИМЕР
Какими свойствами обладает отношение j=<Ф,X>, где X={1; 2; а},
Ф={<1,1>;<a,a>;<a,2>;<2,2>}.
Определим Ф-1, DX:
Ф-1={<1,1>;<a,a>;<2,a>;<2,2>}
DX={<1,1>;<2,2>;<a,a>}.
Отношение является:
- рефлексивным, так как DXÍФ;
- антисимметричным, так как 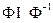 ÍDX;
ÍDX;
- транзитивным, так как Ф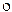 Ф={<1,1>;<a,a>;<a,2>;<2,2>}ÍФ;
Ф={<1,1>;<a,a>;<a,2>;<2,2>}ÍФ;
- несвязное, так как X2DX={<1,2>;<1,a>;<2,1>;<2,a>;<a,1>;<a,2>}Ë Ф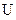 Ф-1={<1,1>;<a,a>;<a,2>;<2,2>;<2,a>}.
Ф-1={<1,1>;<a,a>;<a,2>;<2,2>;<2,a>}.
Отношение называется отношением эквивалентности, если оно рефлексивное, симметричное и транзитивное.
Отношение называется отношением нестрогого (частичного) порядка (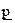 ), если оно рефлексивное, антисимметричное и транзитивное.
), если оно рефлексивное, антисимметричное и транзитивное.
Отношение называется совершенно нестрого порядка (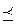 ),если оно рефлексивное, антисимметричное, транзитивное и связное.
),если оно рефлексивное, антисимметричное, транзитивное и связное.
Отношение называется строго порядка (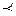 ), если оно антирефлексивное, антисимметричное и транзитивное.
), если оно антирефлексивное, антисимметричное и транзитивное.
Отношение называется совершенно строго порядка (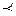 ), если оно антирефлексивное, транзитивное и связное.
), если оно антирефлексивное, транзитивное и связное.
1.4. Решетки.
1.4.1 Диаграммы Хассе.
Рассмотрим отношение частичного порядка: “быть подмножеством“ на множестве-степени М={1,2}.
j=<F,M>, где
Ф={<{Æ},{Æ}>;<{Æ},{1}>;<{Æ},{2}>;<{Æ},{1,2}>;<{1},{1}>;<{1},{1,2}>;<{2},{2}>;<{2},{1,2}>};<{1,2},{1,2}>}.
Графически данное отношение можно изобразить следующим образом:
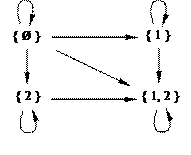 |
РИС 10 Графическое изображения отношения
Отношение является рефлексивным (графически это отображается петлями), антисимметричным (графически - однонаправленные стрелки), транзитивным (графически - транзитивными замыканиями вида:
Для отношений частичного порядка применимы диаграммы Хассе, которые строятся на основе обыкновенной диаграммы следующим образом:
1. рефлексивные петли и транзитивные связи не изображаются;
2. большие элементы (элементы, в которые входят стрелки) располагают выше.
Таким образом, диаграмма Хассе для вышеприведенного примера будет выглядеть следующим образом:
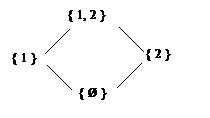 |
РИС 11 Диаграмма Хассе
Для частично упорядоченного множества справедливо следующее:
1. Элемент аÎА называется наибольшим (наименьшим), если для всех хÎ А выполняется x 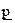 a (a
a (a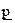 x). Если наибольший (наименьший) элемент существует, то он единственный.
x). Если наибольший (наименьший) элемент существует, то он единственный.
2. Элемент аÎА называется максимальным (минимальным), если нет а множестве А элементов, больших (меньших), чем а. Максимальных (минимальных) элементов может быть несколько.
3. Пусть ВÍА. Элемент аÎА называется можарантой (минорантой), если для всех х Î В этот элемент является наибольшим (наименьшим).
4. Множество мажорант В образует верхнюю границу множества В. Множество минорант В образует нижнюю границу множества В.
5. Наименьший элемент верхней границы называется точной верхней границей, или supremum (sup) B. Наибольший элемент нижней границы называется точной нижней границей, или infimum (inf) B.
6. Частично упорядоченное множество, у которого для любой пары элементов определен и существует sup и inf, называется решеткой.
ПРИМЕР
Пусть дано отношение, представленное на диаграмме Хассе
 |
РИС 12 Диаграмма Хассе
Отношение А не является решеткой, т.к. элементы 7 и 8 не имеют sup.
Отношение В является решеткой, т.к. любая пара имеет sup и inf.
1.4.2 Алгебраическое представление решеток.
Введем обозначения: sup(a,b)=a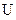 b, inf(a,b)=a
b, inf(a,b)=a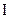 b. Для решетки справедливы следующие свойства:
b. Для решетки справедливы следующие свойства:
1. Коммутативный:
a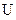 b=b
b=b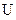 a a
a a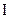 b=b
b=b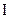 a
a
2. Ассоциативный:
а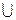 (в
(в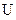 с)=(а
с)=(а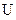 в)
в)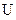 с а
с а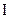 (в
(в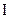 с)=(а
с)=(а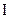 в)
в)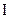 с
с
3. Идемпотентности:
а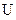 а=а а
а=а а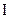 а=а
а=а
4. Поглощения:
а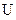 (а
(а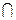 в)=а а
в)=а а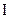 (а
(а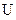 в)=а
в)=а
Решетки, для которой выполняется дистрибутивный закон:
а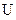 (в
(в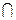 с)=(а
с)=(а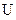 в)
в)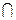 (а
(а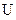 с) а
с) а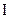 (в
(в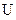 с)=(а
с)=(а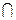 в)
в)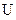 (а
(а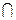 с)
с)
называется дистрибутивной решеткой.
Решетка называется ограниченной, если он имеет максимальный и минимальный элемент.
ПРИМЕР
 |
РИС 13 Диаграмма Хассе решетки
Решетка не является дистрибутивной, т.к. для элементов {2;3;4} не выполняется дистрибутивный закон:
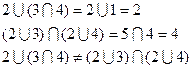
Дана решетка j=<F,M>,
где М={x½0<x<1}, Ф={<x,y>½x<y}. Эта решетка не является, так как не определен максимальный элемент (0.9999999999....) и минимальный элемент (0.0000000...1).
Обозначим в ограниченной решетке максимальный элемент 1, а минимальный элемент 0. Элемент 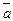 называется дополнением элемента а в данной решетке, если
называется дополнением элемента а в данной решетке, если 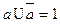 и
и 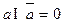 . Решетка называется с дополнением, если каждый элемент имеет хотя бы одно дополнение.
. Решетка называется с дополнением, если каждый элемент имеет хотя бы одно дополнение.
ПРИМЕР
Рассмотрим решетку, представленную на рис. 13. Найдем дополнения для каждого элемента решетки
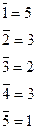
Данная решетка является решеткой с дополнением.
Ограниченная дистрибутивная решетка с дополнением называется булевой решеткой.
На рис. 14 представлены дистрибутивные решетки
 |
РИС. 14. Примеры булевых решеток
2. МАТЕМАТИЧЕСКАЯ ЛОГИКА
2.1. Высказывания
2.1.1. Высказывания и операции над высказываниями.
Высказыванием называется повествовательное предложение, о котором можно сказать истинно оно или ложно.
1. Москва - столица России.
2. Если студент учится на отлично, то он получит красный диплом.
3. Осадки - это снег или дождь.
4. Курица – не птица.
5. Пейте томатный сок.
6. Я лгу.
7. 23<5
Высказываниями являются 1, 2, 3,4 и 7 предложения. Предложение 5 не является высказыванием, так как про него нельзя сказать истинно оно или ложно. Предложение 6 является логическим парадоксом.
Элементарным высказыванием называется высказывание, которое содержит одно утверждение (предложения 1,7).
Сложное (составное) высказывание состоит из элементарных высказываний связанных с помощью следующих предлогов и частиц: И, НЕ, ИЛИ, ЕСЛИ - ТО, ТОГДА И ТОЛЬКО ТОГДА и другие. Предложения 2,3,4 являются сложными высказываниями.
2.1.2. Операции над высказываниями.
Отрицанием высказывани я х называется новое высказывание, которое истинно, если высказывание ложное и наоборот. Таблица истинности операции отрицания имеет вид:
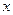
| 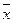
|
Дизъюнкцией двух высказываний x и y(логическое «или») называется новое высказывание, которое будет истинным тогда когда, когда хотя бы одно из высказываний будет истинным.
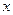
| 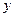
| 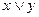
|
Конъюнкцией двух высказываний x и y(логическое «и») называется новое высказывание, которое будет истинным тогда когда, когда оба высказывания истины. Обозначение операции конъюнкция - & (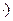
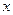
| 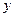
| 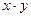
|
Импликацией двух высказываний x и y(«если – то») называется новое высказывание, которое ложно тогда, когда х(предпосылка) - истинно, а у(следствие) - ложно.
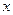
| 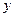
| 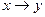
|
Эквивалентностью двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно, если высказывания х и у будут одновременно истинны или ложны.
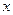
| 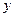
| 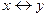
|
Неодназночностью (суммой по модулю два) двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно тогда когда одно из высказываний х или у истинно, а другое ложно.
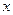
| 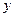
| 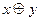
|
Штрих Шеффера (логическое «и - не») высказываний x и y - это новое высказывание, которое будет ложно тогда и только тогда когда оба высказывания истинны.
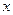
| 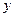
| 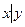
|
Стрелка Пирса (логическое «или - не») высказываний x и y - это новое высказывание, которое будет истинно тогда и только тогда когда оба высказывания ложны.
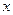
| 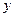
| 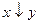
|
Для операций справедливы следующие приоритеты: ù, &, Ú, ®, «.
2.2. Формулы математической логики.
Формулой математической логики называется сложное высказывание, которое получено из элементарных высказываний с использованием логических операций.
Две формулы равносильны, если они принимают одинаковые логические значения на любом наборе значений входящих в формулу элементарных высказываний. Равносильность формул обозначается - A º B.
2.2.1. Формулы равносильности.
1) Коммутативность
АVВ º ВVА А&В º В&А
2) Ассоциативность
АV(ВVС) º (АVВ)VС А&(В&С) º (А&В) &С
3) Дистрибутивность
АV(В&С) º (АVВ)&(АVС) А&(ВVС) º (А&В)V(А&С)
4) Идемпотентность
АVА º А А&А º А
5) Поглощение
АV(А&В) º А А&(АVВ) º А
6) Закон де Моргана
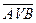 º
º 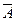 &
&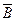
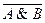 º
º 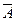 V
V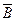
7) Закон исключающий третьего
АV1 º 1 А&1 º A
8) Закон противоречия
AVÆ º A A&Æ º Æ
9) Закон двойного отрицания
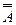 º A
º A
10) 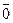 º 1,
º 1, 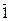 º 0
º 0
11) A®B º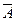 VB
VB
12) A«B º (A®B)&(B®A)
13) AÅB º A&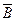 V
V 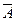 &B
&B
14) A | B º 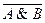 º
º 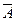 V
V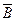
15) A¯B º 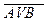 º
º 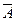 &
&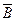
ПРИМЕР
Доказать: 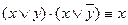
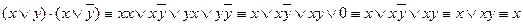
2.3. Представление произвольной функции алгебры логики в виде формулы алгебры логики
Пусть 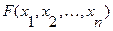 - произвольная функция алгебры логики
- произвольная функция алгебры логики 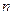 переменных.
переменных.
Рассмотрим формулу
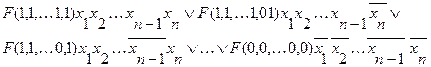 (2.1)
(2.1)
которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции 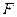 при некоторых определенных значениях переменных
при некоторых определенных значениях переменных 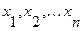 , остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0..
, остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0..
Вместе с тем формула (2.1) содержит в виде логических слагаемых всевозможные конъюнкции указанного вида.
Ясно, что формула (2.1)полностью определяет функцию 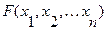 . Иначе говоря, значения функции
. Иначе говоря, значения функции 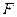 и формулы (2.1) совпадают на всех наборах значений переменных
и формулы (2.1) совпадают на всех наборах значений переменных 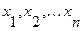 . То есть функция
. То есть функция
Составление формул по таблице истинности. 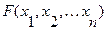 может быть представлена в виде:
может быть представлена в виде:
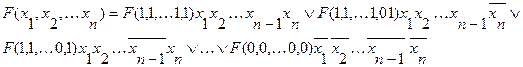 (2.2)
(2.2)
ПРИМЕР Пусть функция 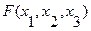 имеет следующую таблицу истинности:
имеет следующую таблицу истинности:

| 
| 
| 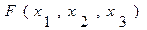
|
Тогда функция 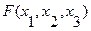 может быть определена в следующем виде:
может быть определена в следующем виде:

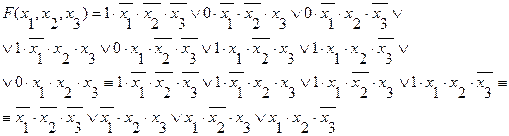
Нетрудно заметить, что для определении функции берутся только те наборы переменных 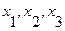 , при которых функция принимает значения 1, что значительно упрощает процедуру определения функции
, при которых функция принимает значения 1, что значительно упрощает процедуру определения функции 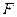 .
.
Формула (2.1) обладает свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию 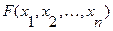 .
.
2. Все логические слагаемые формулы различны.
3. Ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание.
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
5. Перечисленные свойства называются свойствами совершенства.
2.4. Различные формы представления высказываний
Литерой - называется элемент высказывания x или её отрицание.
Элементарной дизъюнкцией называется выражение следующего вида:
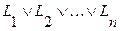 , (2.2)
, (2.2)
где 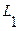 - литера.
- литера.
Элементарной конъюнкцией называется выражение следующего вида:
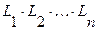 , (2.3)
, (2.3)
Дизъюнктивной нормальной формой (ДНФ) формулы  называется выражение вида:
называется выражение вида:
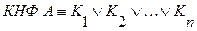 , (2.4)
, (2.4)
где 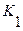 - элементарная конъюнкция.
- элементарная конъюнкция.
Конъюнктивной нормальной формой (КНФ) формулы  называется выражение вида:
называется выражение вида:
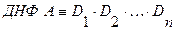 , (2.5)
, (2.5)
где 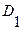 - элементарная дизъюнкция.
- элементарная дизъюнкция.
Любую формулу можно представить в виде ДНФ или КНФ.
ПРИМЕР
Пусть дана формула
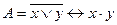
Требуется получить ДНФ и КНФ данной формулы.
Применяя формулы равносильности, получаем КНФ  :
:
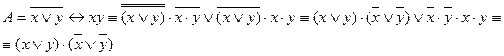
Применяя формулы равносильности, получаем ДНФ  :
:
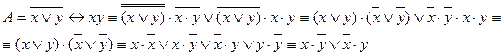
Совершеннойдизъюнктивной нормальной формой(СДНФ) формулы  называется такая ДНФ, для которой выполняются следующие условия:
называется такая ДНФ, для которой выполняются следующие условия:
1. Все элементарные конъюнкции, входящие в ДНФ  , различны.
, различны.
2. Все элементарные конъюнкции, входящие в ДНФ  , содержат литеры, соответствующие всем переменным.
, содержат литеры, соответствующие всем переменным.
3. Каждая элементарная конъюнкция, входящая в ДНФ  , не содержит двух одинаковых литер.
, не содержит двух одинаковых литер.
4. Каждая элементарная конъюнкция, входящая в ДНФ  , не содержит переменную и ее отрицание.
, не содержит переменную и ее отрицание.
СДНФ  можно получить двумя способами:
можно получить двумя способами:
1. по таблице истинности;
2. с помощью равносильных преобразований.
Первый способ получения СДНФ  рассмотрен выше. Рассмотрим второй способ, который состоит в следующем:
рассмотрен выше. Рассмотрим второй способ, который состоит в следующем:
С помощью равносильных преобразований формулы  получают ДНФ
получают ДНФ  . При этом в полученной ДНФ возможны следующие ситуации:
. При этом в полученной ДНФ возможны следующие ситуации:
1. Элементарная конъюнкция  ДНФ
ДНФ  не содержит переменную
не содержит переменную 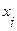 , тогда используются следующие равносильные преобразования:
, тогда используются следующие равносильные преобразования:
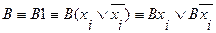
2. Если в ДНФ  входят две одинаковые элементарные конъюнкции, то используя следующее равносильное преобразование:
входят две одинаковые элементарные конъюнкции, то используя следующее равносильное преобразование:
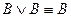 ,
,
одну элементарную конъюнкцию можно отбросить.
3. Если элементарная конъюнкция  ДНФ
ДНФ  содержит одновременно переменную
содержит одновременно переменную 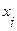 и ее отрицание, то используя следующие равносильные преобразования:
и ее отрицание, то используя следующие равносильные преобразования:
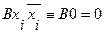 ,
,
эту элементарную конъюнкцию можно отбросить
4. Если элементарная конъюнкция  ДНФ
ДНФ  содержит дважды переменную
содержит дважды переменную 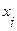 , то используя следующее равносильное преобразование:
, то используя следующее равносильное преобразование:
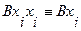 ,
,
одну переменную 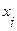 можно отбросить
можно отбросить
СДНФ формулы  существует в единственном виде.
существует в единственном виде.
ПРИМЕР
Получить СДНФ формулы 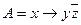
С помощью равносильных преобразований получаем СДНФ  :
:
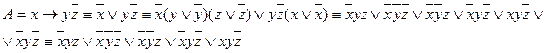
С помощью таблицы истинности получаем СДНФ  :
:
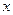
| 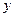
| 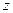
| 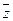
| 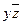
| 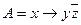
|
СДНФ 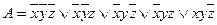
Очевидно, что в результат двух способов совпадает.
Совершеннойконъюнктивной нормальной формой(СКНФ) формулы  называется такая КНФ, для которой выполняются следующие условия:
называется такая КНФ, для которой выполняются следующие условия:
1. Все элементарные дизъюнкции, входящие в КНФ  , различны.
, различны.
2. Все элементарные дизъюнкции, входящие в КНФ  , содержат литеры, соответствующие всем переменным.
, содержат литеры, соответствующие всем переменным.
3. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит двух одинаковых литер.
, не содержит двух одинаковых литер.
4. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит переменную и ее отрицание.
, не содержит переменную и ее отрицание.
СКНФ  можно получить двумя способами:
можно получить двумя способами:
1. по таблице истинности;
2. с помощью равносильных преобразований.
По первому способу по таблице истинности получаем СДНФ 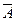 , а СКНФ
, а СКНФ  можно получить, следуя следующему правилу
можно получить, следуя следующему правилу
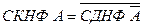
С помощью равносильных преобразований формулы  получают КНФ
получают КНФ  . При этом в полученной КНФ возможны следующие ситуации:
. При этом в полученной КНФ возможны следующие ситуации:
1. Элементарная дизъюнкция  КНФ
КНФ  не содержит переменную
не содержит переменную 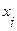 , тогда используются следующие равносильные преобразования:
, тогда используются следующие равносильные преобразования:
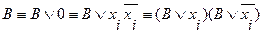
2. Если в КНФ  входят две одинаковые элементарные дизъюнкции, то используя следующее равносильное преобразование:
входят две одинаковые элементарные дизъюнкции, то используя следующее равносильное преобразование:
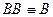 ,
,
одну элементарную дизъюнкцию можно отбросить.
3. Если элементарная дизъюнкция  КНФ
КНФ  содержит одновременно переменную
содержит одновременно переменную 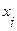 и ее отрицание, то используя следующие равносильные преобразования:
и ее отрицание, то используя следующие равносильные преобразования:
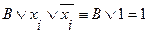 ,
,
эту элементарную дизъюнкцию можно отбросить.
4. Если элементарная дизъюнкция  КНФ
КНФ  содержит дважды переменную
содержит дважды переменную 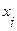 , то используя следующее равносильное преобразование:
, то используя следующее равносильное преобразование:
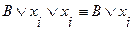 ,
,
одну переменную 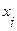 можно отбросить.
можно отбросить.
СКНФ формулы  существует в единственном виде.
существует в единственном виде.
ПРИМЕР
Получить СКНФ формулы 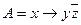
С помощью равносильных преобразований получаем СКНФ  :
:
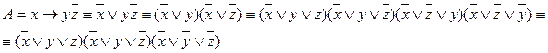
С помощью таблицы истинности получаем СДНФ  :
:
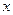
| 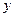
| 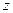
| 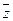
| 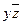
| 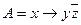
| 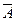
|
СДНФ 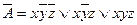
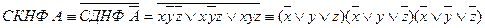
Очевидно, что в результат двух способов совпадает.
СДНФ формулы  можно получить из СКНФ
можно получить из СКНФ  , используя следующее правило:
, используя следующее правило:
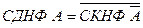
2.5. Выполнимость формулы алгебры логики
Все формулы алгебры логики делятся на три класс:
1. тождественно истинные или тавтологии:
2. тождественно ложные или противоречия;
3. выполнимые.
Формулу называют тождественно истинной (тавтологией), если она принимает значение истинно при любых значениях входящих в нее переменных.
Формула называется тождественно ложной (противоречие), если она принимает значение ложно при любых значениях переменных входящих в нее.
Формула  называется выполнимой, если она принимает значение истинно хотя бы один раз на любом наборе значений входящих в нее переменных и не является тождественно истинной..
называется выполнимой, если она принимает значение истинно хотя бы один раз на любом наборе значений входящих в нее переменных и не является тождественно истинной..
Тождественно истинная формула не имеет СКНФ, а ложная СДНФ.
ПРИМЕР
Формула 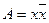 является тождественно ложной:
является тождественно ложной:
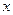
| 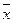
| 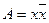
|
Формула 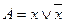 является тождественно истинной:
является тождественно истинной:
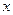
| 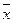
| 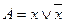
|
Формула 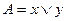 является выполнимой:
является выполнимой:
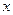
| 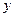
| 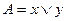
|
Очевидно, что тождественно ложная формула не имеет СДНФ, а тождественно истинная – СКНФ. Выполнимая формула алгебры логики имеет СДНФ и СКНФ,
2.6. Применение математической логики.
С помощью алгебры логики можно:
· решать логические задачи;
· реализация технических устройств.
С помощью алгебры логики можно решать логические задачи. Суть применения методов алгебры логики к решению логических задач состоит в том, что, имея конкретные условия логической задачи, необходимо записать их в виде формулы логики. В дальнейшем путем равносильных преобразований упрощают полученную формулу. Простейший вид формулы, как правило, приводит к ответу на все вопросы задачи.
ПРИМЕР
Определить, Был ли Смит убийцей, если известно следующее:
Если Джонс не встречал этой ночью Смита, то либо Смит был убийцей, либо Джонс лжет. Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство было совершено после полуночи, то либо Смит был убийцей, либо Джонс лжет.
Составим элементарные высказывания:
А – Джонс не встречал Смит этой ночью.
В – Смит был убийца.
С – Джонс лжет.
D – убийство было совершено после полуночи.
Тогда сложные высказывания можно записать на языке алгебры логики в следующем виде:
Если Джонс не встречал этой ночью Смита, то либо Смит был убийцей, либо Джонс лжет. -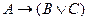
.Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. - 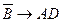
Если убийство было совершено после полуночи, то либо Смит был убийцей, либо Джонс лжет. - 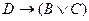
Вся картина преступления может быть представлена в виде формулы:
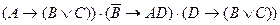
Упростим полученную формулу с помощью равносильных преобразований:
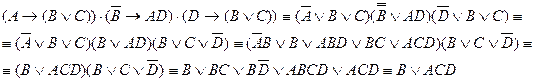
Ответ 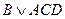 трактуется так: Либо Смит был убийцей, либо убийство совершено после полуночи Джонс лжет, что видел Смита этой ночью. Последнее сложное высказывание (
трактуется так: Либо Смит был убийцей, либо убийство совершено после полуночи Джонс лжет, что видел Смита этой ночью. Последнее сложное высказывание (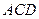 ) по сути также определяет вину Смита, как и прямое утверждение, что Смит был убийцей (
) по сути также определяет вину Смита, как и прямое утверждение, что Смит был убийцей ( ). Таким образом приговор Смиту вынесен.
). Таким образом приговор Смиту вынесен.
В техническом аспекте математическая логика применяется в технических средствах автоматизации в виде релейно-контактных схем (РКС) и логических элементов «и-не», «или-не».
РКС представляют собой переключатели, которые могут находиться либо замкнутом состоянии (1), либо в разомкнутом состоянии (0).
Логические элементы «и-не» осуществляют логическую функцию:
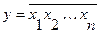
Логические элементы «или-не» осуществляют логическую функцию:
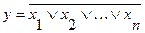
Нетрудно заметить, что суть и РКС, и логических элементов – это формулы математической логики. Суть применения методов алгебры логики к конструированию технических средств автоматизации на базе РКС технического устройства, необходимо записать принцип его работы в виде формулы логики. В дальнейшем путем равносильных преобразований упрощают полученную формулу. Далее полученную формулу реализуют на базе РКС или логических элементов.
Важным требованием при конструировании технических средств автоматизации является минимальное количество базовых элементов(РКС, логических элементов). Поэтому задача минимизации сложных высказываний является особо актуальной.
2.7. Минимизация сложных высказываний.
Существует несколько способов минимизации сложных высказываний. Рассмотрим самые распространенные:
· метод Квайна;
· карты Вейча;
· минимизирующие карты.
2.7.1. Метод Квайна.
Алгоритм метода Квайна включает в себя следующие этапы:
1. Любая формула  приводится к СДНФ.
приводится к СДНФ.
2. СДНФ приводится к сокращенной ДНФ (СкДНФ). При получении СкДНФ используются следующие формулы равносильности:
а) Формула склеивания
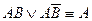
б) Формула неполного склеивания
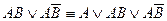
в) Формула поглощения
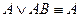
Применяя все возможные процедуры склеивания, СДНФ приводится к СкДНФ.
3. Минимальная форма формулы  (МДНФ
(МДНФ  ) получается на основе импликантной матрицы путем нахождения минимального покрытия этой матрицы. Импликанта – это элементарная конъюнкция СкДНФ. Конституента единицы – это элементарная конъюнкция СДНФ. Импликантная матрица – это матрица импликант и констиуент единиц. (столбцы - конституенты единицы, строки – импликанты). МДНФ может быть несколько.
) получается на основе импликантной матрицы путем нахождения минимального покрытия этой матрицы. Импликанта – это элементарная конъюнкция СкДНФ. Конституента единицы – это элементарная конъюнкция СДНФ. Импликантная матрица – это матрица импликант и констиуент единиц. (столбцы - конституенты единицы, строки – импликанты). МДНФ может быть несколько.
ПРИМЕР.
Необходимо найти МДНФ формулы:
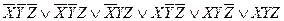
1 2 3 4 5 6
Осуществляем всевозможные склеивания
1-2 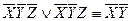
1-4 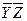
2-3 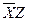
3-6 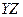
4-5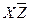
5-6 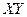
СкДНФ имеет вид:
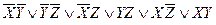
Составляем импликантную матрицу
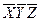
| 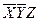
| 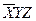
| 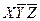
| 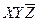
| 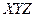
| |
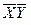
| + | + | ||||
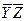
| + | + | ||||
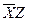
| + | + | ||||
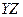
| + | + | ||||
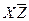
| + | + | ||||
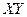
| + | + |
По данной импликантной матрице можно выбрать следующие МДНФ
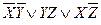
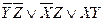
2.7.2. Метод минимизирующих карт.
Алгоритм метода минимизирующих карт включает в себя следующие этапы:
1. Любая формула приводится к СДНФ.
2. Составляется таблица всевозможных сочетаний переменных.
3. Из таблицы вычеркиваются те строки, которые не содержат конституенты СДНФ. Конъюнкции этих строк вычеркиваются в других строках.
4. В каждой строке оставляются конъюнкции с минимальным количеством переменных.
5. Из каждой строки выбирается олна конъюнкция и составляется ДНФ.
6. Из построенных ДНФ выбирается минимальная.
ПРИМЕР
Дана СДНФ
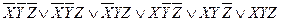
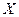
| 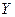
| 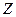
| 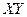
| 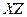
| 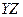
| 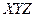
| |
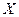
| 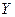
| 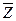
| 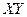
| 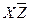
| 
| 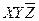
| |
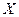
| 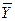
| 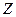
| 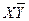
| 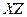
| 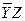
| 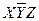
| * |
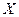
| 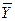
| 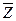
| 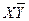
| 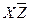
| 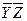
| 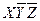
| |
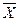
| 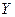
| 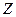
| 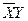
| 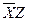
| 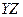
| 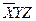
| |
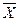
| 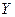
| 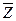
| 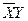
| 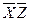
| 
| 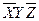
| * |
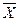
| 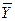
| 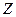
| 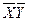
| 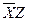
| 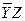
| 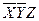
| |
| 
| 
| 
| 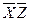
| 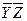
| 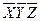
|
* - помечены строки, не содержащие конституенты СДНФ.
После соответствующих преобразований получаем следующую таблицу
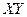
| 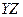
| ||||||
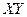
| 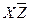
| ||||||
| * | |||||||
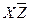
| 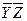
| ||||||
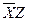
| 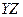
| ||||||
| * | |||||||
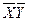
| 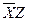
| ||||||
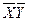
| 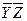
|
После всевозможного перебора остаются следующие МДНФ: