Метод Калмана

Рис.3. Переходная характеристика статического двухъемкостного объекта.

Значения Т₁ и Т₂ определяются следующим образом:

,

,

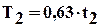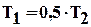при h(0,5T₂)≥0,3K.

Недостатки рассмотренных графических методов аппроксимации h(t) очевидны: не всегда можно определить точку перегиба h(t), возможно неоднозначное проведение касательной, не учитывается форма и характер остальной h(t). Однако, графические методы просты в применении и не требуют значительных затрат времени на реализацию.

4. Аппроксимация переходных функций объектов, содержащих интегрирующие звенья. При известной форме входного сигнала x(t) по виду переходной характеристики нетрудно установить наличие в исследуемом объекте интегрирующих звеньев.

В общем случае дифференциальное уравнение движения выходной координаты объекта с интегрирующими свойствами y(t) записывается в виде:

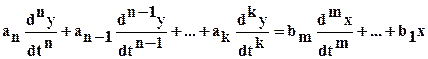, (13)

где n ≥ m; 0 < k < n; обычно k не больше 2;

a_k, a_k+1, …, a_n – постоянные коэффициенты;

b₁, b₂, …, b_m – постоянные величины, некоторые из них могут быть равны нулю, но b₀ ≠0.

Тогда аппроксимирующая передаточная функция W(p) имеет вид:

,

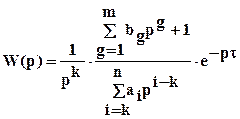где τ – время чистого запаздывания.

Уравнение (13) легко привести к уравнению (1), подставив 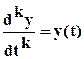. Порядок нового уравнения будет равен n-k, и для определения его n-k+m неизвестных коэффициентов применяются любые из рассмотренных методов аппроксимации переходных характеристик.

Рассмотрим более простой метод аппроксимации – графический.

В случае, если переходная характеристика изменяется с постоянной скоростью, начиная с момента нанесения возмущения x(t)=A, динамические свойства объекта описываются передаточной функцией W(p) вида:

,

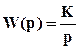где К=tgα / A – отношение тангенса угла наклона функции h(t) к амплитуде входного воздействия А.

Если скорость изменения выходной координаты устанавливается с некоторым запаздыванием τ, которое равно орезку оси абсцисс, отсекаемому асимптотой, проведённой к h(t).

В общем случае в качестве аппроксимирующей передаточной функции W(p) используется:

.

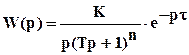Для нахождения неизвестных K, T и n из графика h(t) определяют угол наклона α асимптоты к оси абсцисс, величины h_u и T_u=τ (рис. 4).

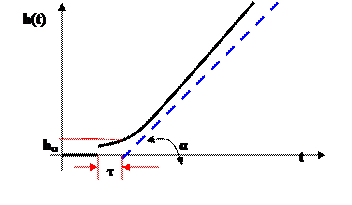Рис. 4. Определение параметров интегрирующей W(p)объекта.

Затем рассчитывается К=tgα/A, а из номограмм, приведённых в [2], находятся T и n.

n

n

T_u/T

h_u/KT_u

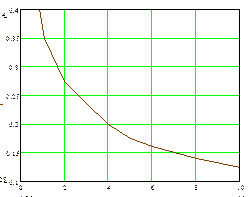
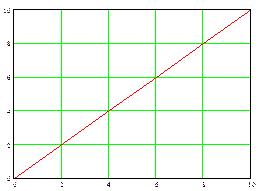
Одним из сравнительно несложных современных методов динамической идентификации, основанных на результатах пассивного эксперимента, является метод Калмана. Сущность его заключается в следующем:

1. В процессе эксплуатации через строго фиксированные интервалы времени записывают значения входных и выходных параметров;

2. Выбирают наиболее простой вид аналитической модели, записанной в виде разностного уравнения n – го порядка;

3. По результатам эксперимента и принятого типа модели МНК определяют коэффициенты разностного уравнения;

4. Решают разностное уравнение и сравнивают полученные динамические характеристики с экспериментом;

5. При больших отклонениях задаются разностным уравнением более высокого порядка и повторяют расчёт.

Разностное уравнение первого порядка имеет вид:

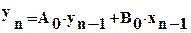, (14)

где n – номер точки эксперимента;

х_n-1 – соответствует установившемуся значению у_уст исследуемого параметра;

А, В – коэффициенты разностного уравнения.

Если модель первого порядка (1) не адекватна, в качестве модели используется уравнение второго порядка:

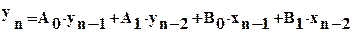. (15)

Тогда модель (1) описывается дифференциальным уравнением первого порядка:

,

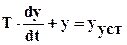решением которого является:

,

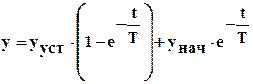где, полагая у=у_n, у_нач=у_n-1 и t=n·∆t, при n=1 получаем:

,

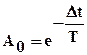откуда рассчитывается постоянная времени процесса:

.

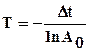Дата добавления: 2013-12-12