Дифференциальное уравнение первого порядка

Общие сведения на основании понятия о Д.У.

VIII. Дифференциальные уравнения (Д.У.)

Лекция 11.

При решении различных задач в различных областях науки, в том числе в экономике, часто используют математические модели, при описании которых применяют уравнения, связывающие независимую переменную, искомую функцию и ее производные. Такие уравнения и называются дифференциальными. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Так решением уравнения 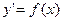является функция 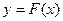– первообразная для функции .

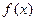Если искомая неизвестная функция зависит от одной переменной, то Д.У. называют обыкновенным, в противном случае Д.У. в частых производных. Далее будем рассматривать только обыкновенные Д.У. наивысший порядок производной, входящей в Д.У. называется порядком этого уравнения (например 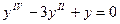- обыкновенное уравнение четвертого порядка). Процесс нахождения решения Д.У. называется его интегрированием.

В качестве примера решения задач с использованием Д.У. можно, например, рассмотреть уравнение Циолковского. Обозначим скорость ракеты в некоторый момент времени 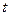через 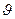а массу 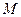-. пусть в этот момент времени включается двигатель, причем скорость выхлопных газов равна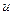. Через время 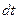масса ракеты уменьшается и станет равной 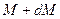, а скорость увеличится и станет равной 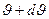. Сравним импульс системы ракеты + выхлопные газы в моменты времен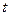и и 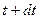. Первый равен 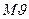, второй 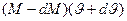– импульс выхлопных газов. Итоговое уравнение примет вид (согласно закону сохранения импульса) .

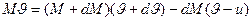Пренебрегая бесконечно малой второго порядка 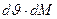, получим:

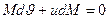или 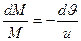– это дифференциальное уравнение с разделенными переменными. Решая его методом интегрирования получим 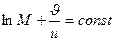, считая 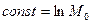. Получим 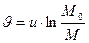. Эта формула определяет изменение скорости ракеты в зависимости от изменения ее массы (формула Циолковского).

Дифференциальное уравнение первого порядка в общем случае можно записать в виде:

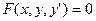(1)

Уравнение связывает независимую переменную х, искомую функцию у и ее производную у’, если это уравнение можно разрешить относительно у’, то его записывают в виде:

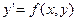(2)

и называют Д.У. первого порядка, разрешенным относительно производной. Последнее уравнение устанавливает между координатами точки 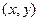и угловым коэффициентом у’ касательной к интегральной кривой, проходящей через эту точку. Следовательно, Д.У. 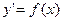даст совокупность направлений (поле направлений) на плоскости ОХУ. Таково геометрическое истолкование Д.У. первого порядка.

Кривая, во всех точках которой направление поля одинаково называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить что 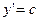, т.е. .

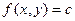Д.У. первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:

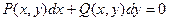
где 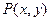и 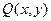– известные функции. Последнее уравнение удобно тем, что переменные х и у в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.

Интегрирование Д.У. в общем случае приводит к бесконечному множеству решений, отличающихся друг от друга на постоянные величины.

Чтобы решение Д.У. приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям. Условие, что при х=х₀ функция у должна быть равна заданному числу у₀ называется начальным условием. Начальное условие записывается в виде:

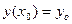или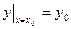

Общим решением Д.У. первого порядка называется функция 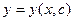, содержащая одну произвольную постоянную и удовлетворяющая условиям:

1) Функция 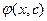является решением Д.У. при каждом фиксированном значении .

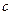1) Каково ни было начальное условие, можно найти такое значение постоянной 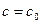, что функция 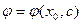удовлетворяет данному начальному условию.

Частым решением Д.У. первого порядка называется любая функция 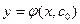, полученная из общего решения 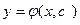при конкретном значении постоянной .

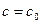Если общее решение Д.У. найдено в неявном виде, т.е. в виде уравнения 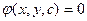, то такое уравнение называется общим интегралом Д.У. Уравнение 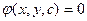в этом случае, называют частным интегралом уравнения.

С геометрической точки зрения 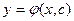есть семейство интегральных кривых на плоскости ХОУ, а частное решение 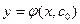– одна кривая из этого семейства, проходящая через точку .

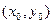Задача нахождения решения Д.У. первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.

Теорема 8.1. Существование и единственность решения задачи Коши.

Если в уравнении (2) функция 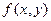ее частная производная 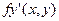непрерывны в некоторой области 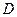, содержащей точку 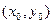, то существует единственное решение 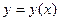этого уравнения, удовлетворяющее начальным условиям.

Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая Д.У., проходящая через точку .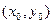

1. Уравнения с разделяющимися переменными

Наиболее простым Д.У. первого порядка является уравнение вида:

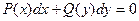(3)

В этом уравнении первое слагаемое зависит от х, а второе от у. Проинтегрировав почленно это уравнение, получим:

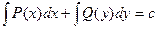- это общий интеграл.

Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:

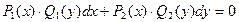(4)

Особенности этого уравнения заключаются в том, что коэффициенты при и представляют собой произведения двух функций, одна из которых зависит только от х, а другая от у. уравнение (4) легко сводится к уравнению (3) путем почленного деления его на 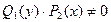. При этом получим:

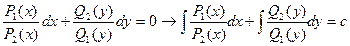- общий интеграл.

1) При проведении почленного деления Д.У. на 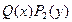могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение 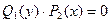и установить те решения Д.У., которые не могут быть получены из общего решения, так называемые – особые решения.

2) Уравнение 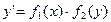также сводится к уравнениям, разделяющимися переменными. Для этого достаточно положить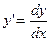и разделить переменные.

3) Уравнени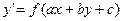е , где 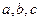– числа, путем замены 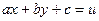сводится к Д.У. с разделяющимися переменными. Дифференцируя по х, получим:

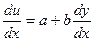, т.е.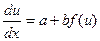

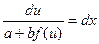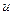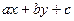Откуда – интегрируя это уравнение и заменяя на , получим общий интеграл исходного уравнения.

Примеры:

1) Найти общий интеграл уравнения 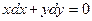. Интегрируя, получим 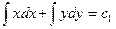или 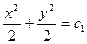. Обозначив 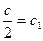, получим 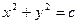– общий интеграл Д.У.

2) 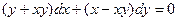, преобразуем левую часть. 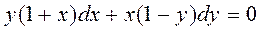. Делим на 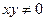. Интегрируя, получим 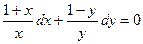. 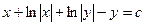или 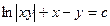. Поскольку 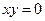по условию решения, то решения 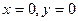является особыми решениями и не входят в общий интеграл.

2. Однородные дифференциальные уравнения

К уравнениям с разделяющимися переменными приводятся однородные Д.У. первого порядка.

Функция 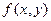называется однородной функцией n-го порядка, если при умножении каждого ее аргумента на произвольный множитель х вся функция умножается на хⁿ, т.е.

.

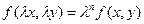Например, функция 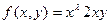есть однородная функция второго порядка, поскольку

.

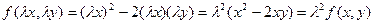Дифференциальное уравнение называется однородным, если функция 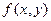есть однородная функция нулевого порядка.

Покажем, что однородное Д.У. можно записать в виде:

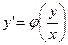(4)

Если 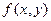– однородная функция нулевого порядка, то по определению 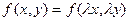. Положив 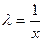получим:

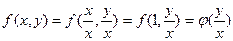
Однородное уравнение (4) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной 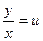или, что то же самое .

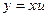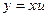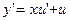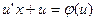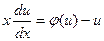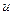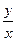Действительно, подставив и в уравнение (4), получаем или , т.е. уравнение с разделяющимися переменными. Найдя его общее решение следует заменить в нем на . Получим общее решение исходного уравнения.

Однородное уравнение часто задается в дифференциальной форме:

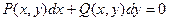(5)

Это уравнение будет однородным, есл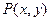и и 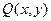– однородные функции одинакового порядка.

Переписав (5) в виде 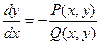и применив в правой части рассмотренное выше преобразование, получим уравнение 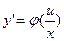. При интегрировании уравнений (5) нет необходимости предварительно приводить их к виду (4). Подстановка 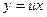сразу преобразует уравнение (5) в уравнение с разделяющимися переменными.

Пример:

Найти общий интеграл уравнения.

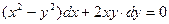- это однородное уравнение. Положим 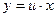, тогда 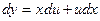и получим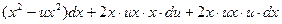

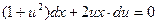- это уравнение с разделяющимися переменными, поэтому 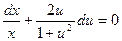после интегрирования получим 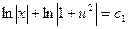или .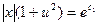

Если 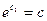, то 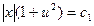, переходя к старым неизвестным, получим 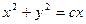– решение этого уравнения.

3. Линейные уравнения

Д.У. первого порядка называется линейным, если его можно записать в ви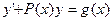де: , где 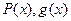– заданные функции и в частности постоянные.

Особенность этих Д.У. заключается в том, что искомая функция у и ее производная входят в уравнение первой степени не перемножаясь между собой.

Рассмотрим два метода решения этих уравнений. Методы Бернулли и Лагранжа.

Дата добавления: 2013-12-12