Системы дифференциальных уравнений

Для решения многих практических задач в различных областях науки и техники нередко требуется использовать не одну, а много функций. Нахождение этих функций может привести к нескольким ДУ, каждое из которых содержит независимую переменную. Совокупность всех этих ДУ и образует систему. Системой ДУ называется совокупность ДУ каждое из которых содержит независимую переменную, искомые функции и их производные. Общий вид системы ДУ первого порядка, содержащей n искомых функций 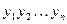, следующий:

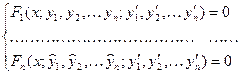
Система ДУ первого порядка, разрешенных относительно производной, т.е. система вида

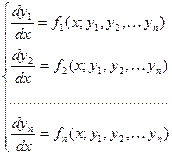(1)

Называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций.

Замечание: Во многих случаях системы уравнений и уравнения высших порядков можно свести к нормальной системе (1).

Так система трех ДУ второго порядка

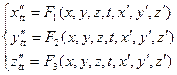
описывающая движение точки в пространстве, путем введения новых переменных 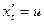, 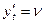и 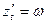можно привести к нормальной системе ДУ.

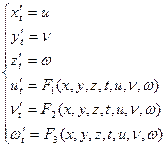
Подобную операцию можно производить и с системами уравнений, содержащих производные более старшего порядка. Отсюда следует полезность изучения именно нормальных систем.

Решением системы (1) называется совокупность из n функций 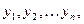удовлетворяющих каждому из уравнений этой системы. Начальные условия для системы (1) имеют вид 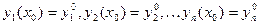. (2)

Задача Коши для системы ставится так: найти решение системы уравнений (1) удовлетворяющее начальным условиям (2).Условия существования и единственность решения определяется теоремой Коши.

Теорема Коши: Если в системе (1) все функции непрерывны вместе со своими частными производными по 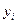в некоторой области 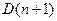- мерного пространства, то в каждой точке 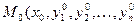этой области существует, и притом единственное, решение 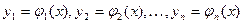системы, удовлетворяющее начальным условиям (2).

Меняя в области Д точку 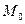(т.е. начальные условия) получим бесчисленное множество решений, которое можно записать в виде решения зависящего от n произвольных постоянных: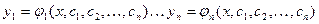

Это решение является общим, если по заданным начальным условиям (2) можно однозначно определить постоянные 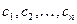, из системы уравнений

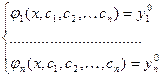
Решение, получающееся из общего, при конкретных значениях постоянных (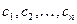) называется частным решением системы (1).

1. Решение нормальных систем.

Одним из основных методов решения нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача – переход от ДУ к системе – рассмотрена ранее) Сам метод основан на следующих соображениях: пусть задана система нормальных ДУ (1).Продифференцируем по х любое, например, первое уравнение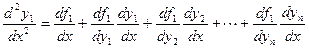

Подставив в это равенство значение производных 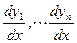из системы (1) получим

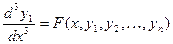. Продолжая этот процесс (дифференцируем- подставляем- получаем) найдем: 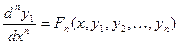. Соберем все уравнения в систему

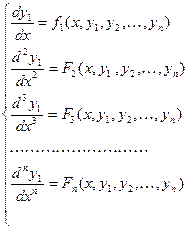(3)

Из первых (n-1) уравнений системы (3) выразим функции 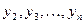через 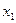функцию 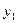и ее производные 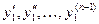. В результате получим:

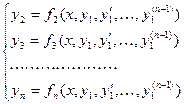(4)

Найденные значения 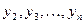подставим в последнее из уравнений системы (3).Получим одно ДУ n-го порядка относительно искомой функции y

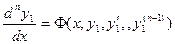. Пусть его решение есть .

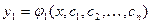Продифференцировав его (n-1) раз и подставив значения производных 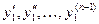в уравнения системы (4) найдем функции .

.

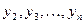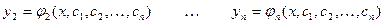Пример: Решить систему уравнений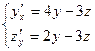

Продифференцируем первое уравнение: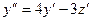, подставляем 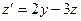в полученное равенство .

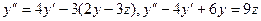Составим систему уравнений 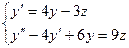. Из первого уравнения системы выражаем z через y и 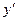: 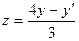(5)

Подставляем z во второе уравнение последней системы:

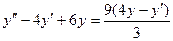т.е.

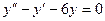
Получили ЛОДУ второго порядка. Решаем его: характеристическое уравнение имеет вид

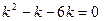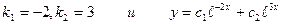,- общее решение уравнения.

Найдем функцию z.Значения 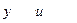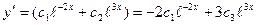подставим в выражение z через 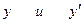(5).Получим: .

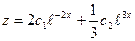Таким образом, общее решение данной системы уравнений имеет вид:

, .

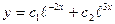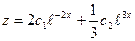Дата добавления: 2013-12-12