
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Замечание
|
|
|
|
Эллипс
КРИВЫЕ ВТОРОГО ПОРЯДКА
Рассмотрим линии, определяемые уравнениями сторой степени относительно текущих координат
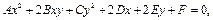 (16.1)
(16.1)
где 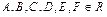 и
и 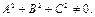 Такие линии называют кривыми второго порядка. Позже мы докажем, что уравнение (16.1) определяет на плоскости эллипс, гиперболу, параболу, пару прямых (параллельных, совпадающих, пересекающихся) или пустое множество. В лекциях 16-17 рассмотрим свойства эллипса, гипеболы и параболы.
Такие линии называют кривыми второго порядка. Позже мы докажем, что уравнение (16.1) определяет на плоскости эллипс, гиперболу, параболу, пару прямых (параллельных, совпадающих, пересекающихся) или пустое множество. В лекциях 16-17 рассмотрим свойства эллипса, гипеболы и параболы.
Def. Эллипсом называется геометричекое место точек плоскости, сумма расстояний от которых до двух данных точек (фокусов), есть величина постоянная (большая, чем расстояние между фокусами).
Обочначим сумму расстояний до фокусов 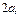 а расстояние между фокусами (фокальное расстояние) – а расстояние между фокусами (фокальное расстояние) – 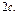 Пусть Пусть 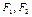 – фокусы эллипса. – фокусы эллипса.
| 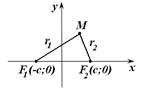 Рис. 16.1
Рис. 16.1
|
Выберем декартову систему координат так, чтобы 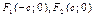 (рис. 16.1). В нашем случае
(рис. 16.1). В нашем случае 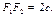 Пусть
Пусть 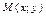 – текущая точка эллипса.
– текущая точка эллипса. 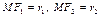 – фокальные радиусы.
– фокальные радиусы.
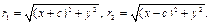 Тогда:
Тогда:
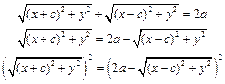
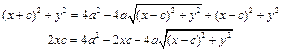
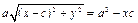 (16.2)
(16.2)
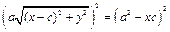
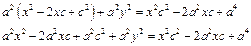
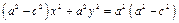 (16.3)
(16.3)
Заметим, что по определению эллипса 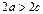 , т.е.
, т.е. 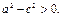 Обозначим
Обозначим
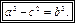 (16.4)
(16.4)
Тогда (16.3) принимает вид:
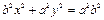
Разделим обе части полученного уравнения на 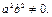 Получим:
Получим:
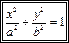 (16.5)
(16.5)
Уравнение (16.5) называют каноническим уравнением эллипса.
Исследуем форму эллипса.
1. Очевидно, что 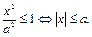 Аналогично,
Аналогично, 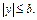 Следовательно. точки эллипса лежат внутри прямоугольника, ограниченного прямыми
Следовательно. точки эллипса лежат внутри прямоугольника, ограниченного прямыми 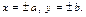
2. Найдем точки пересечения эллипса с осями координат. Положим 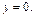 Из уравнения (16.5) получим
Из уравнения (16.5) получим 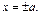 Т.е. точки
Т.е. точки 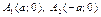 – точки пересечения с осью
– точки пересечения с осью 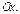 Положив в уравнении (16.5)
Положив в уравнении (16.5) 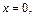 находим точки пересечения эллипса с осью
находим точки пересечения эллипса с осью 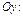
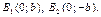
Def. Точки 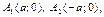
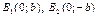 называют вершинами эллипса. Отрезки
называют вершинами эллипса. Отрезки 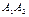 и
и 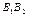 , а также их длины
, а также их длины 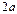 и
и 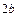 называются соответственно большой и малой осями. Числа
называются соответственно большой и малой осями. Числа 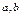 называются соответственно большой и малой полуосями.
называются соответственно большой и малой полуосями.
3. Если точка 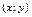 принадлежит эллипсу, то точки принадлежит эллипсу, то точки 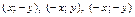 также принадлежат эллипсу. Отсюда следует симметрия эллипса относительно координатных осей и начала отсчета. Центр симметрии эллипса называют еще центром эллипса, т. е. для эллипса, заданного уравнением (16.5), точка также принадлежат эллипсу. Отсюда следует симметрия эллипса относительно координатных осей и начала отсчета. Центр симметрии эллипса называют еще центром эллипса, т. е. для эллипса, заданного уравнением (16.5), точка
| 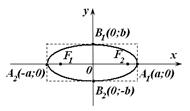 Рис. 16.2
Рис. 16.2
|
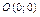 – центр эллипса.
– центр эллипса.
|
|
|
4. Из уравнения (16.5) следует, что если 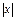 возрастает от 0 до
возрастает от 0 до 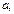 то
то 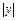 будет уменьшаться от
будет уменьшаться от 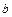 до 0 и наоборот.
до 0 и наоборот.
Таким образом, эллипс имеет форму, изображенную на рис. 16.2.
1. Если 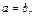 то уравнение (16.5) принимает вид
то уравнение (16.5) принимает вид 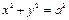 – уравнение окружности с центром в начале отсчета и радиусом
– уравнение окружности с центром в начале отсчета и радиусом 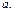 В этом случае согласно (16.4)
В этом случае согласно (16.4) 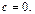 Следовательно, фокусы эллипса совпадают с центром окружности. Таким образом, окружность можно считать частным случаем эллипса.
Следовательно, фокусы эллипса совпадают с центром окружности. Таким образом, окружность можно считать частным случаем эллипса.
2. Если фокусы эллипса принадлежат оси 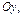 то уравнение эллипса имеет тот же вид, но
то уравнение эллипса имеет тот же вид, но 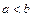 и
и 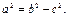 В этом случае
В этом случае 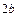 – большая ось, а
– большая ось, а 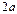 – малая ось.
– малая ось.
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 262; Нарушение авторских прав?; Мы поможем в написании вашей работы!