Вынужденные колебания. Резонанс

Колебания системы, которые совершаются за счет работы периодически меняющейся внешней силы, называются вынужденными.

Пусть на систему действует внешняя сила, меняющаяся со временем по гармоническому закону: 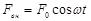, где F₀ – амплитуда силы (максимальное значение), w – угловая частота колебаний вынуждающей силы. Тогда уравнение движения будет иметь вид: =.

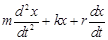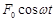Разделим обе части этого уравнения на m и введем вновь обозначения: 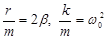, тогда получим неоднородное дифференциальное уравнение второго порядка: 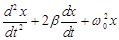= 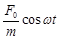(1)

Решение этого уравнения, как известно из высшей математики, представляет собой сумму свободных и вынужденных колебаний: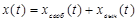

Таким образом, вынуждающая сила раскачивает систему, сообщая ей запас энергии, и пополняет расходуемую энергию, поддерживая колебательное движение. В первый момент система совершает помимо вынужденных еще свободные колебания. Частота свободных колебаний определяется по известной формуле: 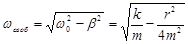. Эти колебания затухают, и устанавливаются колебания, частота которых равна частоте вынуждающей силы, то есть вынужденные колебания. Когда работа вынуждающей силы сравнивается с энергией потерь, колебания становятся установившимися. Амплитуда этих колебаний должна быть постоянной, если постоянна амплитуда вынуждающей силы.

Решение дифференциального уравнения при установившемся движении имеет вид: 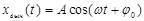(2)

где А, j – величины, которые требуется определить, w – круговая частота колебаний внешней переменной силы. Подставляя (2) в (1), получаем искомые величины:

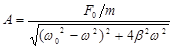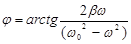(3) (4)

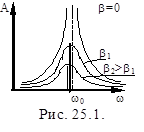Амплитуда колебаний зависит от амплитуды и частоты внешних сил. При некоторой частоте внешних сил знаменатель в выражении (3) будет иметь минимальное значение, а амплитуда вынужденных колебаний – максимальное значение. Эта частота называется резонансной. Для ее нахождения, приравниваем к нулю производную:

,

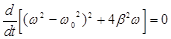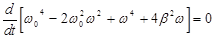
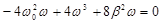
Сократим на 4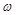: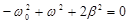, откуда получим: .

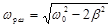Резонансная амплитуда: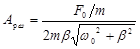

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте w₀, называется резонансом.

При коэффициенте затухания b=0, когда отсутствуют силы сопротивления, 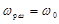, а А_рез становится бесконечно большой. На рисунке 25.1. даны зависимости амплитуды колебаний от частоты вынуждающей силы. Отдельные кривые соответствуют различным значениям коэффициента затухания b. Эти кривые называются резонансными. Чем меньше коэффициент затухания, тем резче изменяется амплитуда вынужденных колебаний. При резонансе наступают наиболее благоприятные условия для поступления энергии в колеблющуюся систему от источника внешней силы. Увеличение амплитуды происходит до тех пор, пока вся работа внешней силы не сравняется с энергией потерь.

Тема 20. Волны. Уравнение волны. Энергия волны

Процесс распространения колебаний в среде называется волновым процессом (или волной). Все разнообразие волн в природе и технике подразделяют на два типа: волны механические (упругие) и электромагнитные.

Упругими (или механическими) волнами называются механические возмущения, распространяющимися в упругой среде.

Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения. Поперечные волны возникают при деформациях сдвига.

Скорость распространения продольных волн в тонком стержне 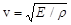, где Е – модуль Юнга, r – плотность среды.

Скорость распространения поперечных волн в изотропном твердом тел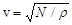е , где 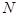– модуль сдвига.

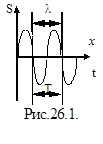Скорость распространения продольных (звуковых) волн в жидкости и в газе 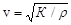, где К – модуль объемной упругости среды, r – плотность среды. Например, в воздухе: 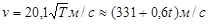, где Т – термодинамическая температура, измеренная по шкале Кельвина, t – температура, измеренная по шкале Цельсия.

При распространении колебаний в среде частицы не перемешаются вместе с волной, а лишь колеблются около своих положений равновесия. Поступательно перемещаются лишь фаза и энергия колебаний.

Графически волну изображают так же, как и колебания (рис.26.1).

Геометрическое место точек, колеблющихся в одинаковых фазах, называется волновой поверхностью. В зависимости от формы волновой поверхности различают сферические, плоские, цилиндрические волны. Геометрическое место точек, до которых доходят колебания с одинаковой фазой к некоторому моменту времени t, называется фронтом волны. Фронт волны является частным случаем волновой поверхности.

Пусть плоская волна распространяется вдоль оси х (рис.26.1). Эта волна характеризуется: длиной волны, периодом, амплитудой, частотой, фазовой скоростью.

Расстояние, на которое определенная фаза распространяется за один период колебания, называется длиной волны l. Из рисунка видно, что l – это наименьшее расстояние между точками, колеблющимися в одинаковых фазах. Скорость распространения волны - фазовая скорость. Фазовая скорость – равна скорости перемещения в пространстве точек поверхности, соответствующей любому фиксированному значению фазы.

.

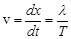Волна, распространяющаяся в пространстве от какого-либо источника, называется бегущей волной.

Уравнением волны называется алгебраическое выражение, которое дает зависимость смещения колеблющейся точки s как функция ее координат (х) и времени t: .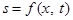

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси 0Х, имеет вид: 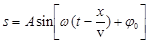, (2)

где 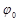– начальная фаза колебаний; 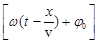– фаза плоской бегущей волны.

Для характеристики волн используется волновое число k, характеризующее скорость изменения фазы в пространстве

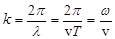. (3)

Учитывая (3), уравнение (2) примет вид: 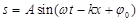(4)

Уравнение волны, распространяющейся вдоль отрицательного направления оси 0Х, отличается от (4) знаком члена kx.

Из условия 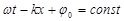получаем выражение для фазовой скорости: .

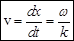Дата добавления: 2013-12-12