Теплообмен при перекрестном движении газа и материала

Теплообмен в неподвижном плотном слое. (Задача Шумана)

Внутренняя задача тепломассообмена

Внешняя задача тепломассообмена

Процессы тепломассоообмена

При рассмотрении внешней задачи предположим, что внутри частицы градиента температуры и концентрации пренебрежимо малы по сравнению с соответствующими градиентами во внешнем потоке. В этом случае поток тепла или вещества можно найти с помощью уравнений баланса тепла и массы для внешнего течения. Поскольку тепловые и диффузионные процессы аналогичны, в дальнейшем использовали термины массопередачи. Рассматриваемый случай соответствует практике металлургического производства, поскольку растворимость многих газов (N₂, H₂, O₂) в жидких металлах обычно невелика. В этом случае коэффициент распределения имеет большие значения и согласно уравнению

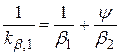
или .

Растворимость газов в молекулах описывается законом Сиверста

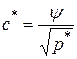, (3.1)

где с^* – равновесная концентрация поглощаемого газа в жидкости, молярная доля; р^* – равновесное парциальное давление поглощаемого газа над раствором; y – коэффициент распределения.

При малой растворимости газа вследствие медленного отвода газа от поверхности раздела фаз в глубь ванны концентрация газа на поверхности соответствует равновесной с газовой фазой при парциальном давлении Р_S, мало отличающемся от равновесного значения.

Примем, что частицу обтекает осесимметричный поток с заданным полем скоростей. Представим уравнение конвективного переноса в виде

В безразмерном виде уравнение конвективного переноса имеет вид:

. (3.2)

Краевые условия для внешней задачи массообмена имеют вид:

начальные

(3.3)

граничные (постоянство концентраций примеси на поверхности частицы и в потоке)

(3.4)

В уравнении (3.2) левая часть характеризует конвективный перенос вещества, правая – молекулярную диффузию. Соотношение между конвективным и диффузионным переносом вещества, характеризует критерий Пекле. При малых значениях критерия Пекле перенос вещества конвекцией пренебрежимо мал, по сравнению с молекулярной диффузией, что имеет метол при малой скорости движения потока и (или) малом размере частицы. При больших значениях критерия Пекле определяющим является конвективный перенос.

Критерий Пекле 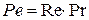в задачах теплообмена, или в задачах массообмена.

Массообмен при умеренных значениях критерия Пекле (1£Ре£10³)

При умеренных значениях критерия Пекле система уравнений (3.2-3.4) решается численным методом, а результаты решения затем аппроксимируются расчетной формулой.

Для газового пузырька (), движущегося при Re<1, численные решения этих уравнений для значений Ре<10³ с точностью 2-3% аппроксимируются формулой

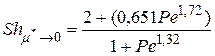, (3.5)

где Sh – число Шервуда, ; d – диаметр частицы, d=2r_o.

Для твердой сферической частицы (m^*®¥)

. (3.6)

Для капли справедлива формула

, (3.7)

где иопределяется по формулам (3.5) и (3.6) при фиксированных значениях Ре.

Увеличение коэффициента массоотдачи (критерия Шервуда) с ростом критерия Пекле определяется процессом формирования диффузионного пограничного слоя в лобовой части сферической частицы Увеличение критерия Ре ведет к уменьшению толщины образующегося диффузионного пограничного слоя, что в свою очередь, согласно формуле

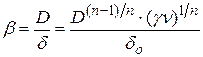
приводит к увеличению коэффициента массоотдачи b.

Массоперенос при больших значениях критерия Пекле (Ре>10³)

При больших значениях критерия Пекле с достаточной для рпак4тических расчетов точностью процесс переноса можно считать установившимся и рассматривать его в приближении диффузионного пограничного слоя, уравнение (3.2) принимает вид

. (3.8)

Уравнение (3.8) совместно с граничными условиями (3.4) можно решить аналитически, для чего его следует привести к уравнению Лапласа, воспользовавшись уравнением Прантдля–Мизеса. Последнее предполагает переход от переменных R, q к y, q, где – безразмерная функция тока. Учитывая, что в пограничном слое сферической частицы (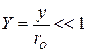), разложим безразмерную функцию тока вблизи поверхности частицы в ряд Тейлора

(3.9)

и сохранили лишь первый неисчезающий член.

Из уравнения (3.9) получили выражение для переменной Прандтля– Мизеса

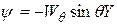. (3.10)

Переменная Прандтля–Мизеса для твердой среды

. (3.11)

Введение новых переменных позволяет значительно упростить уравнение (3.8) и свести его у уравнению Лапласа

, (3.12)

где .

В новых переменных граничные условия имеют вид:

; (3.13)

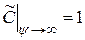. (3.14)

Полагая, что в точке набегания потока на сферу (точка q=0) концентрация вещества такая же, как на бесконечности, запишем

. (3.15)

Решение уравнения (3.12) с граничными условиями (3.13) – (3.15) имеет вид

, (3.16)

где l_о – значение l при q=0.

Зная величину потока вещества, можно определить коэффициент массопередачи

и величину числа Шервуда

. (3.17)

Внутренняя задача тепломассообмена предполагает, что сопротивление переносу сосредоточено внутри частицы и изменением концентрации во внешнем потоке можно пренебречь.

Исследование внутренней задачи тепло- и массообмена можно провести на примере обтекания осесимметричным потоком капли на основании уравнения конвективного переноса полагая, что значения компонентов вектора скорости известны.

.

Пусть в начальный момент времени концентрация растворенного в апле вещества постоянна по объему, тогда без ограничения общности краевые условия можно представить в виде

(3.18)

Такая задача рассмотрена только для капли, движущейся при Ре>>1, когда известны точные значения компонентов вектора скорости жидкости внутри капли. В предельном случае Ре®0 массо- и теплоперенос описывается уравнением нестационарного молекулярного переноса, решение которого можно получить разделением переменных в уравнении Лапласа. Полученное Ньюменом выражение для средне концентрации вещества в частице имеет вид

.

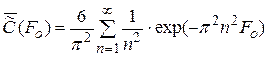Из формулы следует, что средняя концентрация вещества в капле уменьшается экспоненциально с течением времени (увеличение критерия F_o).

Выражение для средней концентрации вещества в капле имеет вид:

, (3.19)

где B_n, l_n – численные коэффициенты.

При F_o®¥ ряд быстро сходится и можно ограничиться первым членом ряда. При F_o®0 ряд сходится крайне медленно и при малых значениях F_o обычно используют численные методы решения (3.2) с краевыми условиями (3.1).

Найдем среднее значение коэффициента массоотдачи. За dt количество экстрагируемого вещества . Эту же величину потока асссы можно выразить как

.

Приравняв эти выражения, получим

.

Интегрируя это соотношение и вводя средний по времени коэффициент массоотдачи 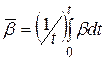, получили

или .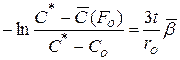

Используя величину степени извлечения А, последнее выражение можно представить в виде

. (3.20)

Учитывая, что диффузионный критерий Фурье имеет вид и используя выражение (3.20), получили зависимость для среднего значения числа Шервуда

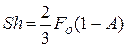. (3.21)

Рассмотрим процесс нагрева неподвижного слоя, состоящего из термически тонких частиц, одномерным потоком газа, движущимся вдоль оси у, принимая следующие допущения: слой состоит из частиц одинакового размера; теплообмен между потоком и слоем определяется законом Ньютона; коэффициент a_F одинаков по высоте и сечению слоя; теплофизические свойства частиц и газа не зависят от температуры; передача тепла в газе и в слое теплопроводностью отсутствует; поток газа равномерно распределен по сечению слоя. При принятых допущениях уравнения теплового баланса для элемента слоя объемом 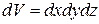и протекающего через этот элемент газа будут иметь вид:

; (3.22)

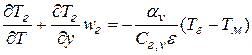, (3.23)

где Т_м, Т_г – температура слоя и протекающего через него газа; w_г – скорость газа в стесненном сечении, м/с; С_м,v, С_м,г – удельные объемные теплоемкости материала слоя и газа, дж/(м³ К).

Вводя обозначения

; ; ;

; ,

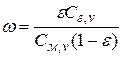где - температура (газа или материала) в начальный момент времени t=0.

Представим исходную систему уравнений в виде

; (3.24)

. (3.25)

Краевые условия для рассматриваемой постановки задачи имеют вид

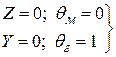(3.26)

Решение систем уравнений (3.24)-(3.26) получено Шуманом и в наиболее удобной форме может быть представлено следующим соотношением:

(3.27)

(3.28)

где 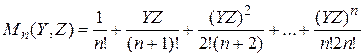- функция Бесселя первого рода нулевого порядка от мнимого аргумента.

Решение Шумана можно использовать и для расчета нагрева (охлаждения) слоя, состоящего из кусков, обладающим термическим сопротивлением.

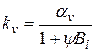. (3.29)

Анализ уравнений (3.27), (3.28) показывает, что температуры слоя и газа меняются по высоте слоя и во времени и зависят от размера частиц, порозности слоя, теплофизических параметров и скорости движения газа.

Перекрестная схема движения материалов и газов имеет место в процессах агломерации, при обжиге и охлаждении окатышей на конвейерных машинах, охлаждении агломерата и окатышей в чашевых охладителях и т.д. Рассмотрим задачу нагрева слоя потоком газа при перекрестном движении материала и газа при тех же допущениях, что и в предыдущей задаче.

Учитывая, что и (рис.) уравнения теплового баланса для элемента слоя объемом 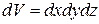и протекающего через этот элемент потока газа для рассматриваемого случая имеет вид:

; (3.30)

. (3.31)

Вводя обозначения

; ;

; ; ,

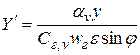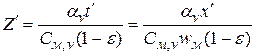где и .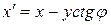

Приведем систему уравнений (3.30) – (3.31) к виду:

,

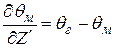с краевыми условиями 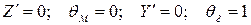, идентичную формулировке задачи Шумана (уравнения 3.24., 3.25, 3.26).

Таким образом, при использовании безразмерной координате и безразмерного времени для решения задач теплообмена при перекрестном движении материала и газа можно применять расчетный аппарат (уравнения 3.27, 3.28). Введение суммарного коэффициента теплопередачи позволяет использовать полученные решения для анализа процессов теплообмена в слое, состоящем из частиц, обладающих термическим сопротивлением.

Дата добавления: 2013-12-12