Массы и плотность звезд

Размеры звезд.

Из-за очень большого расстояния до звезд их диски нельзя разглядеть ни в какие телескопы. Угловые размеры небольшого числа звезд удалось измерить лишь при помощи специальных оптических приборов - звездных интерферометров. В большинстве случаев диаметры звезд оценивают лишь теоретически по известной температуре и светимости.

Известно, что мощность излучения горячего тела (его светимость) L пропорциональна произведению абсолютной температуры Т в четвертой степени на площадь поверхности S. (Закон Стефана - Больцмана.) Для шара S=4pR², где R- радиус. Поэтому выражение для светимости звезды можно записать следующим образом: L=sT⁴ 4pR². (Здесь s - коэффициент пропорциональности, постоянная Стефана – Больцмана равен 5,7 10^-8 Вт/(м²К²).) Для светимости Солнца можно записать аналогичное выражение: L=sT⁴_с 4pR²_с Из этих двух выражений следует 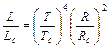Отсюда, зная L и Т звезды, легко найти ее радиус, выраженный в радиусах Солнца, R=R_c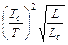Обычно радиус и светимость звезды выражают в солнечных единицах R_с=1 и L_с=1.

Тогда LgR=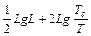

Поперечники самых крупных звезд в 1000 и более раз превосходят солнечный Звезда, открытая в созвездии Кита, в 10 раз меньше Земли по диаметру, а размеры нейтронных звезд порядка десяти километров.

Наиболее важной характеристикой каждой звезды является ее масса. В той или иной степени от массы зависят все остальные свойства звезд. Непосредственно массу можно оценить только по гравитационному воздействию звезды на окружающие тела. Массу Солнца, например, определяют по известным периодам обращения планет. Она примерно равна 2 10³⁰кг. Звезд планеты не видны, и подобным образом оценить их массу нельзя. Но во многих случаях звезды образуют пары, и тогда для оценки массы можно воспользоваться третьим законом Кеплера, зная из наблюдений большие полуоси их орбит и скорости движения.

Для двойных звезд измерения масс показали, что почти во всех случаях они заключены в пределах от 0,1 до 10 масс Солнца. Более массивные звезды, имеющие массу 10—50М_с, в природе крайне редки. Звезды массой меньше 0,1М_с из-за низкой температуры и малого размера почти не излучают света. Поэтому еще неясно, как часто они встречаются в природе.

Самые малые по массе звезды значительно массивнее любой планеты Солнечной системы. Именно большой массой звезд и определяется их способность разогреваться и излучать свет. Даже у самой большой планеты Солнечной системы - Юпитера - масса составляет около 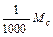Если бы можно было в сотни раз увеличить массу этой планеты, Юпитер превратился бы в звезду.

Независимые измерения масс и светимостей звезд показали, что для большинства из них эти величины связаны друг с другом: светимость приблизительно пропорциональна четвертой степени массы. Иными словами, выполняется примерное равенство: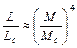

Это означает, что, если звезда имеет массу, вдвое большую, чем Солнце, она излучает примерно в 16 раз больше света.

Используя соотношение между массой и светимостью, можно по известной светимости примерно оценить массу звезды. Для одиночных звезд этот косвенный метод определения массы является практически единственным.

Измерения показали, что звезды не так сильно отличаются друг от друга по массам, как по размерам или светимостям. По этой причине звезды очень большого размера, имея примерно такую же массу, как и остальные, обладают очень низкой средней плотностью вещества. У таких звезд, как Солнце, средняя плотность близка к плотности воды. У звезд-гигантов и сверхгигантов из-за их больших размеров она ничтожно мала - часто значительно ниже, чем плотность воздуха на уровне моря. Но и при такой плотности звезда представляет собой непрозрачный газовый шар.

Из сказанного ясно, что самой высокой средней плотностью должны обладать звезды малых размеров.

Формула LgR=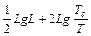связывает между собой три важные характеристики звезды - радиус, светимость и эффективную температуру. Вместе с тем, как мы уже знаем, имеется важная эмпирическая зависимость между спектром, т. е. фактически температурой, и светимостью (диаграмма Герцшпрунга - Рессела). Это значит, что все три величины, входящие в формулу, не являются независимыми и для каждой последовательности звезд на диаграмме спектр - светимость можно установить определенное соотношение между спектральным классом и радиусом. Для того чтобы сделать это соотношение наглядным, изменим несколько диаграмму спектр-светимость. Будем откладывать вместо визуальной абсолютной звездной величены абсолютную болометрическую звездную величину и вместо спектрального класса - логарифм соответствующей эффективной температуры. При этом общий характер диаграммы в основном сохранится. На такой диаграмме положение всех звезд, имеющих одинаковые радиусы, изобразится прямыми линиями, поскольку зависимость между LgL и LgT в формуле линейная. На рис. приведены линии постоянных радиусов, позволяющие легко находить размеры звезды по ее светимости (абсолютной звездной величине) и спектру (эффективной температуре).

Замечательно, что на рис. главная последовательность, а также, в меньшей степени, последовательность сверхгигантов изобразились почти прямыми линиями. Это позволяет установить для данных звезд эмпирическую зависимость между болометрической светимостью и радиусом. Так, например, для большинства звезд главной последовательности выполняется соотношение L=R^5,2

Обнаружена важная эмпирическая зависимость между массой и болометрической светимостью, изображенная на рис. Прямая на этом рисунке изображает зависимость L=M ^3,9

Дата добавления: 2013-12-12