Погрешность численного дифференцирования

Аппроксимируя исследуемую функцию, ее представляют в виде:

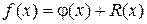. (6)

В качестве j(x) можно принять либо интерполяционную функцию, либо частичную сумму ряда. Тогда погрешность аппроксимации R (x) определяется остаточным членом ряда или P_{n –1}(x). Дифференцируя (6) необходимое число раз находим:

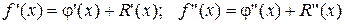и т.д.

Тогда погрешность аппроксимации 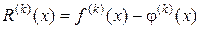при численном дифференцировании функции, заданной таблицей с шагом h зависит от h, и ее записывают в виде О (h^k). Показатель степени k называют порядком погрешности аппроксимации производной. При этом предполагается, что | h | < 1.

Оценку погрешности формул (2) – (5) можно проиллюстрировать с помощью ряда Тейлора.

Пусть дважды непрерывно дифференцируемая функция f (x) задана таблицей значений.

x	x 0	x 1	x 2	…	xn
y	y 0	y 1	y 2	…	yn

Где y_i = f (x_i), i = 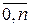. Пусть далее узлы равностоящие, h = (x_n – x ₀)/ n, x_i = x ₀ + ih, .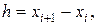

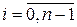Ряд Тейлора в общем виде:

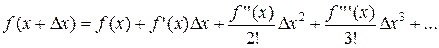(7)

Запишем (7) при x = x ₁, 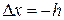с точностью до h ¹:

y ₀ = y ₁ – y' ₁ h + O (h ²).

Тогда y' ₁ = .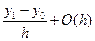

Это выражение совпадает с (2) и является аппроксимацией первого порядка (k = 1). Тогда для произвольного узла .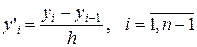

А по всему отрезку [ a, b ], где h = (b - a)/ n для f ' (x) погрешность не превысит величины R = .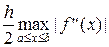

Полагая для (7) D x = h, можно получить этот результат и для соотношения (3). Для оценки погрешности для (4) и (5) воспользуемся рядом Тейлора, полагая D x = – h и D x = h соответственно получим:

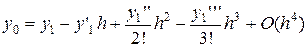; (8)

;

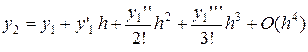в предположении, что f (x) трижды непрерывно дифференцируемая функция.

Вычитая из второго равенства первое, получаем:

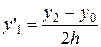+ О (h ²), здесь k = 2.

Для произвольного узла:

.

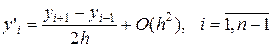На основании (7) по всему отрезку погрешность аппроксимации не превзойдет величины:

.

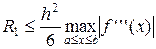Складывая равенства (8) найдем:

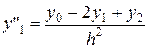+ О (h ²), k = 2.

Для отрезка [ x_{i –1}, x_{i +1}] получим:

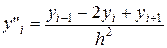, i = .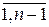

А погрешность на отрезке [ a, b ] для второй производной оценивается соотношением:

.

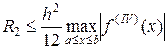Следует отметить, что, вообще говоря, приближенное дифференцирование представляет собой операцию менее точную, чем интерполирование. Считают, что при численном дифференцировании функции y = f (x), заданной таблично, имеют место два типа погрешностей:

а) погрешности усечения, которые вызываются заменой функции y = f (x) интерполяционным многочленом P_n (x);

б) погрешности округления, которые вызываются неточным заданием исходных значений y_i.

При этом известно, что с уменьшением шага численного дифференцирования погрешность округления возрастает, а погрешность же усечения, как правило, убывает. Поэтому при вычислениях по формулам численного дифференцирования стоит задача и оптимального выбора шага h.

Дата добавления: 2013-12-11