Числовые характеристики непрерывного случайного процесса

Функция распределения

Определение. Для непрерывной случайной величины x функция распределения F (x) определяется равенством .

Непосредственно из определения следует равенство . Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению .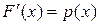

Функция распределения F (x) непрерывной случайной величины x имеет те же свойства, что и функция распределения дискретной случайной величины:

1. F (x) — непрерывная возрастающая функция.

2. ; .

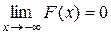Свойства 1 и 2 вытекают непосредственно из определения функции F (x).

3. P (x ₁ < x < x ₂) = F (x ₂) – F (x ₁), т.е. вероятность того, что случайная величина x принимает значение из промежутка (х ₁; х ₂) равна приращению F (x) на этом промежутке.

Таким образом, непрерывную случайную величину можно определить заданием либо плотности распределения р(х), либо функции распределения F(x).

Это те же математическое ожидание М x, дисперсия D x и среднеквадратическое отклонение σξ. Физический смысл этих числовых характеристик, введённых для дискретного случайного процесса, сохраняется и для непрерывного процесса с небольшими изменениями.

Для дальнейшего рассуждения необходимо вспомнить что-то из интегрального исчисления:

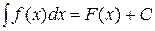неопределённый интеграл

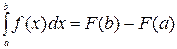определённый интеграл

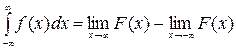несобственный интеграл

Определение. Математическое ожидание М x случайной величины x определяется формулой

в предположении, что интеграл существует (сходится). Ещё раз подчеркнём, смысл математического ожидания как среднего значения случайной величины сохраняется.

Все свойства математического ожидания, приведённые ранее для дискретных случайных величин, имеют место и для непрерывных случайных величин.

Определение. Дисперсия D x непрерывной случайной величины x определяется равенством

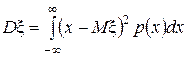
или аналогично дискретным случайным величинам выпишем формулу, удобную для вычислений .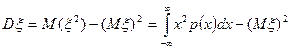

Дисперсия непрерывной случайной величины имеет те же свойства, что и дисперсия дискретной случайной величины.

Определение. Величина σξ называется среднеквадратическим отклонением и также определяется по формуле σξ = .

Задача 1. Случайная величина имеет плотность распределения

.

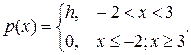Найти параметр h, F (x), P (1<ξ<5), М ξ, D ξ, σξ и построить графики p(x) и F(x).

а) Параметр h определим из условия .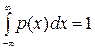

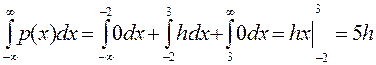, 5 h = 1, отсюда h = 1/5. Следовательно,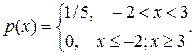

Построим график p(x).

б) Для нахождения вероятности попадания в интервал воспользуемся формулой P (a < ξ < b) = .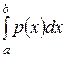

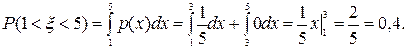
в) Математическое ожидание вычислим по формуле .

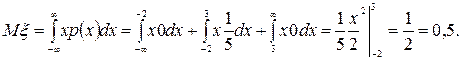
г) Дисперсию вычислим по формуле .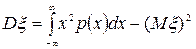

.

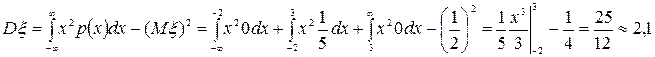д) Среднеквадратическое отклонение σξ=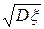≈≈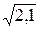 1,5.

е) Построим функцию распределения.

Если x ≤–2, то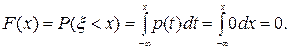

Если –2< x <3, то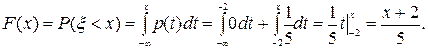

Если x ≥3, то 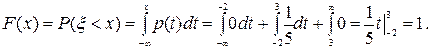Следовательно,

Построим график F (x).

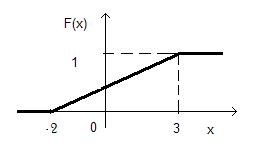Задача 2. Функция распределения случайной величины ξ задана выражением

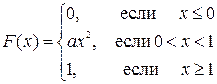
Найти параметр a, p (x), P (0,25<ξ<0,5), P (-1<ξ<2), М ξ, D ξ, σξ и построить графики p(x) и F(x).

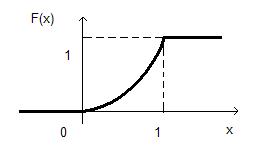
а) Параметр a определим из условия непрерывности функции распределения в точке x =1. Имеем ax= 1, отсюда a= 1. Следовательно,

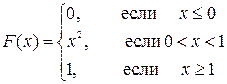
Построим график F (x).

б) Выпишем плотность распределения p (x) по формуле :

.

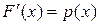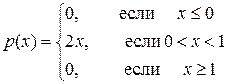Построим график p (x).

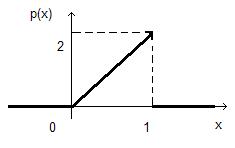в) Для нахождения вероятности попадания значения случайной величины ξ в заданный интервал воспользуемся формулой P (a < x < b) = F (b) – F (a):

P (0,25<ξ<0,5) = F (0,5) – F (0,25) = 0,5² – 0,25² = 0,1875.

P (– 1<ξ<2) = F (2) – F (– 1) = 1 – 0 = 1.

г) Математическое ожидание вычислим по формуле :

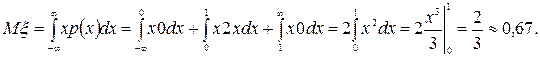
д) Дисперсию вычислим по формуле :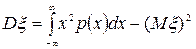

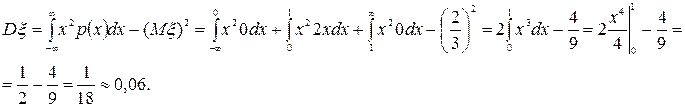
г) Среднеквадратическое отклонение σξ=≈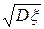

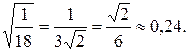
Дата добавления: 2013-12-13