Непрерывные случайные величины: нормальный закон распределения

Определение. Непрерывная случайная величина x называется распределённой по нормальному закону Гаусса, если её плотность распределения 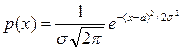, где s>0.

Таким образом, значения а и s полностью определяют функцию р (х).

Для упрощения записи функции p (x) введём функцию 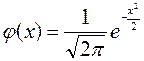. Это чётная и неотрицательная функция. Её график приведён на рисунке ниже.

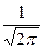
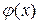
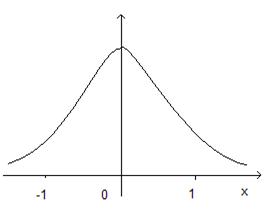
Тогда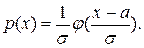

График плотности распределения нормальной случайной величины при 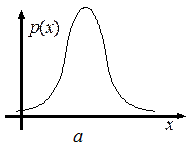некоторых значениях а и s представлен на другом рисунке. График симметричен относительно прямой х = а, и выполняются условия: р (х) ® 0 при х ® ±µ. Если а увеличивать, оставляя s неизменной, то график будет перемещаться вправо, а если а уменьшать, то влево, не изменяя формы.

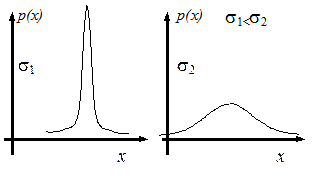Если значение а неизменно, то относительно малому значению s будет соответствовать график р (х) с выраженным пиком, как на левом рисунке. При относительно большом значении s график р (х) представляет собой пологую кривую, как изображено на правом рисунке.

Функция распределения F (x) нормальной случайной величины x выводится обычным способом по формуле: 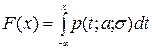. Доказательство опускаем, 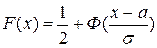, где 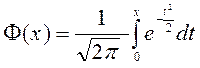— знаменитая интегральная функция Лапласа. Она нечётная и значения её табулированы.

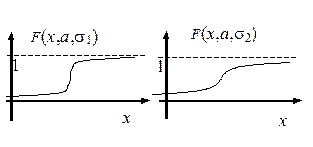Графики функций F (x) для нормально распределённых случайных величин при различных значениях s
изображены на рисунках, s₁<s₂.

Аналогично предыдущему вычисляются Mx и Dx. Выпишем без доказательства: Mx = a ^. и Dx = s².

Таким образом, параметры а и s в формуле для плотности распределения случайной величины, распределённой по нормальному закону, приобретают смысл: а – математическое ожидание, s² – дисперсия.

Вероятность того, что нормально распределённая случайная величина x примет значение из промежутка (х ₁, х ₂) рассчитывается по формуле

, где 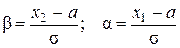. Значения F(х) определяются из таблицы Лапласа.

Если случайная величина x имеет плотность распределения, выражающуюся функцией p (x;0;1), то есть x – нормально распределённая случайная величина с математическим ожиданием, равным нулю, и дисперсией, равной единице, тогда .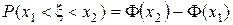

Случайную величину с плотностью распределения p (x;0;1) можно принять за некоторый эталон для случайных величин, распределённых по нормальному закону. График плотности распределения такой случайной величины симметричен относительно оси ординат.

Правило трёх s (трёх “сигм”)

Пусть имеется нормально распределённая случайная величина x с математическим ожиданием, равным а и дисперсией s². Определим вероятность попадания x в интервал (а – 3s; а + 3s), то есть вероятность того, что x принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.

P (а – 3s< x < а + 3s)= Ф (3) – Ф (–3)=2 Ф (3).

По таблице Лапласа находим Ф (3)≈0,49865, откуда следует, что 2 Ф (3) практически равняется единице. Таким образом, можно сделать важный вывод: нормально распределённая случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3s.

Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8, 2,9 или 3,2 и получить тот же вероятностный результат. Учитывая, что Ф (2)≈0,477, можно было бы говорить и о правиле двух “сигм”.

Задача 4. Определитезакон распределения, найдите Mx, Dx и выпишите функцию распределения для случайной величины x, если её плотность распределения есть

.

Задача 5. Случайная величина m имеет следующую плотность распределения вероятностей: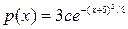. Чему равен параметр с?

Задача 6. Случайная величина n имеет следующую функцию распределения: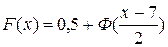. Чему равны

а) математическое ожидание случайной величины n;

б) дисперсия случайной величины n?

Дата добавления: 2013-12-13