Основные свойства линейной системы дифференциальных уравнений

Теорема 1. Линейная комбинация решений однородной системы (3) также является решением этой системы.

Теорема 2. Разность любых двух решений неоднородной системы уравнений (2) есть решение однородной системы (3).

Сумма любого частного решения неоднородной системы (2) и решения соответствующей однородной системы (3) есть решение неоднородной системы (2).

Теорема 3. Если и 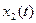- решения систем уравнений

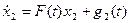
соответственно, то

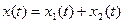- решение системы уравнений

.

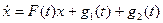Теорема 4. Пусть 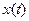() – решение системы уравнений (2), матрица 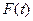и вектор 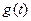непрерывны на отрезке 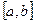. Пусть 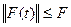(где означает норму матрицы : 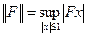) и 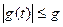. Тогда для 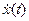имеет место следующая оценка:

(4)

В частности, для линейной однородной системы (3) имеем оценку ():

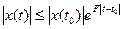(5)

Теорема 5. Пусть матрица 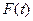системы (2) непрерывна на отрезке 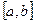и 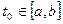. Тогда решение системы (2) однозначно определяется на отрезке 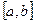условием

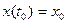. (6)

Итак, из оценки (5) вытекает единственность решения задачи Коши для линейной системы (2) с непрерывной матрицей .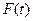

Следствие 1. Пусть матрица 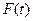непрерывна на отрезке 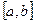, тогда 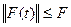и для решения 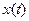однородной системы (3) имеет место оценка

(7)

Иначе говоря, рост функции 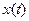ограничен экспонентой.

Следствие 2. Решение 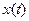однородной линейной системы с непрерывной матрицей 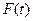тождественно равно нулю, если оно равно нулю в какой либо точке отрезка .

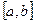Дата добавления: 2013-12-13