Первообразная для функции и неопределенный интеграл от нее

Лекция 35. Понятие неопределенного интеграла. Свойства неопределенного интеграла. Правила интегрирования. Таблица интегралов. Непосредственное интегрирование.

Интегральное исчисление, наряду с дифференциальным исчислением, принадлежит к числу важнейших составляющих высшей математики (вместе они составляют так называемый математический анализ). Это исчисление базируется на понятиях неопределенного и определенного интегралов, введенных в математику Ньютоном и Лейбницем в конце 17-го века параллельно с введением ими же понятий производных и дифференциалов функций.

В дифференциальном исчислении ставилась задача: для данной функции найти ее производную. В интегральном исчислении ставится обратная задача: по производной функции найти саму функцию.

Пусть y = f(x) – некоторая заданная функция.

Определение. Всякая функция y=F(x), производная которой совпадает с функцией y = f(x), называется первообразной для функции y = f(x). То есть если 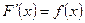, то функция 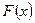будет первообразной для функции f(x) (а f(x) будетпроизводной от своей первообразной F(x)).

Пример1. Функция 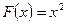является первообразной для функции 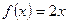, так как .

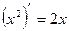Отметим, что функция 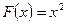- не единственная первообразная для функции 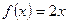. В самом деле, любая функция вида 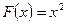+ С, где С – произвольная (неопределенная) константа, тоже будет первообразной для функции 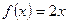. Действительно, .

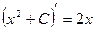И вообще, если F(x) – первообразная для заданной функции f(x), то и все функции вида F(x)+C, где С - неопределенная константа, тоже будут первообразными для функции f(x). Действительно, если 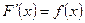, то и .

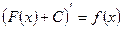Таким образом, найдя какую-либо первообразную F(x) для данной функции f(x), мы сразу можем записать для нее и множество других первообразных:

F(x) + C (С - неопределенная константа) (1)

Более того, мы сейчас докажем, что выражение (1) дает множество всех первообразных для функции f(x).

Действительно, пусть F(x) – какая-либо конкретная первообразная для функции f(x), а 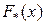– любая другая первообразная для этой же функции f(x). Образуем новую функцию 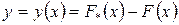и найдем ее производную:

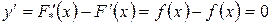
Как оказалось, эта функция 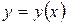имеет нулевую производную для любого 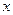. Но, как известно, производная функции характеризует скорость изменения функции. Значит, скорость изменения функции 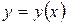для любого х равна нулю. А это значит, что при изменении х функция 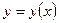не меняется (сохраняет постоянное значение).То есть 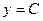, где С - некоторая постоянная. Таким образом, 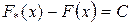, откуда 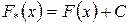. То есть действительно любая первообразная 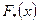для функции 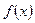находится среди функций (1). Иначе говоря, множество функций (1) действительно представляет собой множество всех первообразных для функций 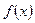. то множество Лейбниц обозначил специальным символом

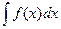(2)

и назвал неопределенным интегралом от функции 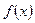. Здесь знак 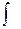- знак неопределенного интеграла; 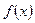- подынтегральная функция; 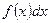- подынтегральное выражение; 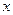- переменная интегрирования.

Так как выражение (2) - это лишь другое обозначение выражения (1), то можно записать:

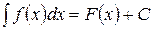(3)

Таким образом, отыскивая (вычисляя) неопределенный интеграл 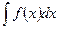, мы тем самым ищем все первообразные 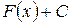для подынтегральной функции 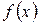. То есть ищем все функции, производные от которых равны 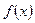. Эти функции (их бесчисленное множество) представляют собой сумму конкретной функции 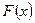(конкретной первообразной для 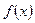) и неопределенной константы С, которой можно придать любое значение. Из-за наличия этой неопределенной константыв равенстве (3) и результат вычисления неопределенного интеграла оказывается неопределенным. Отсюда и термин: неопределенный интеграл.

Если неопределенный интеграл 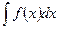найден верно (то есть множество всех первообразных 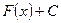для функции 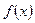найдено верно), то должно выполняться проверочное для (3) равенство:

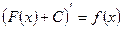(4)

Пример 2.

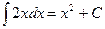- верно, так как .

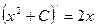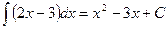- верно, так как .

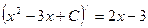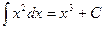- неверно, так как .

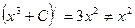Основные свойства неопределенных интегралов .

1. Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции:

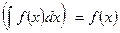(5)

Доказательство. Используя (3) и (4), получим:

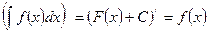
2. Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

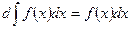(6)

Доказательство. Вспоминая формулу для нахождения дифференциала функции, получим:

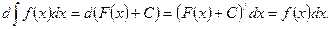
3. Свойство 3. Неопределенный интеграл от дифференциала функции равен этой функции плюс неопределенная константа:

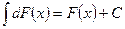(7)

Доказательство:

.

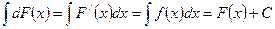4. Свойство 4. Нахождение функции 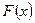по ее дифференциалу 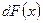: если 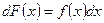, то

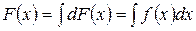. (8)

Доказательство. Если 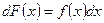, то . А это значит, что функция 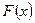является первообразной для функции 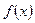. Но этих первообразных для функции 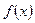имеется бесчисленное количество, и все они находятся посредством вычисления .

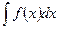Примечание. Функция 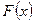определяется по формуле (8) неоднозначно – она определяется с точностью до неопределенной константы С, которая появится после вычисления 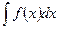. Поэтому для однозначного определения функции 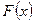по ее дифференциалу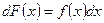нужно задать некоторое дополнительное условие для этой функции. Таким условием, в частности, может быть следующее услови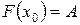е: , где и А - заданные числа.

Пример 3. Найти функцию 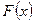, если известно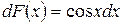, что и что .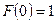

Решение. Используя (8), получаем:

.

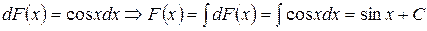Мы получили бесчисленное множество функций :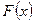

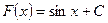(С - неопределенная константа).

Константу С найдем из дополнительного условия :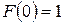

.

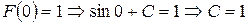Таким образом, получаем окончательно: .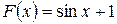

5. Свойство 5. Постоянный множитель можно выносить за знак неопределенного интеграла:

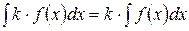(k – константа, k 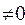) (9)

Доказательство. Рассмотрим правую часть равенства (9):

,

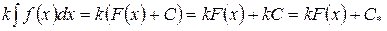где 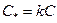- неопределенная константа (если k 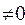). Таким образом, равенство (9) принимает вид:

.

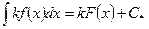А это равенство верно, что подтверждает его проверка:

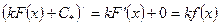
6. Свойство 6. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций:

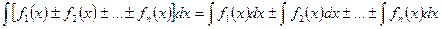(10)

Доказательство. Вычисляя правую часть равенства (10), получаем:

…= =

=

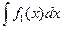
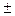
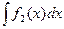
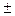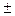
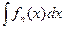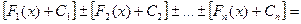
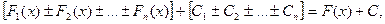
где

.

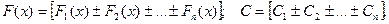Таким образом, доказываемое равенство (10) принимает вид:

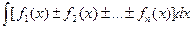= F(x) + C

И оно верно, так как

При вычислении неопределенных интегралов бывает полезно использовать следующие правила:

1. Если 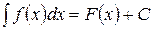, то

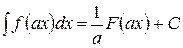. (11)

Действительно, дифференцируя левую и правую части равенства (11), получим:

.

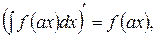
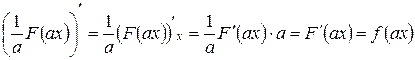Производные от правой и левой частей равны, что и требовалось доказать.

2. Если 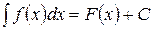, то

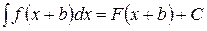. (12)

3. Если 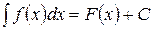, то

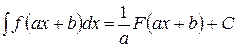. (13)

Равенства (12) и (13) доказываются дифференцированием правой и левой частей равенств.

Пример 4. 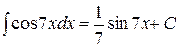(по формуле 11).

Пример 5. 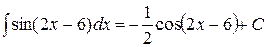(по формуле 13).

Дата добавления: 2013-12-13