Построение линии пересечения двух плоскостей

Две плоскости в пространстве могут быть параллельными или пересекающимися, частным случаем пересекающихся плоскостей являются взаимно перпендикулярные плоскости.

Построение линии пересечения плоскостей - одна из основных задач начертательной геометрии, имеющих большое практическое значение. Она относится к так называемым позиционными задачам.

Позиционными называются задачи на определение общих элементов различных сопрягаемых геометрических форм. К ним относятся задачи на принадлежность геометрических элементов и на пересечение геометрических объектов, например, пересечение прямой и плоскости с поверхностью, пересечение двух поверхностей и, в частности, задача на пересечение двух плоскостей.

Линия пересечения двух плоскостей является прямой, одновременно принадлежащей обеим пересекающимся плоскостям. Поэтому для построения линии пересечения плоскостей необходимо определить две точки этой прямой или одну точку и направление линии пересечения.

Рассмотрим частный случай пресечения плоскостей, когда одна из них проецирующая. На рис. 3.6 приведены плоскость общего положения, - заданная треугольником АВС и горизонтально-проецирующая Р. Двумя общими точками, принадлежащими обеим плоскостям, являются точки D и Е, которые и определяют линию пересечения.

Для определения этих точек были найдены точки пересечения сторон АВ и ВС с проецирующей плоскостью. Построение точек D и Е как на пространственном чертеже (рис. 3.6, а), так и на эпюре (рис. 3.6,б) не вызывает затруднений, т.к. основано на разобранном выше собирательном свойстве проецирующих следов плоскостей.

Соединяя одноименные проекции точек D и Е получим проекции линии пересечения плоскости треугольника АВС и плоскости Р. Таким образом, горизонтальная проекция D₁ Е₁ линии пересечения заданных плоскостей совпадает с горизонтальной проекцией проецирующей плоскости Р – с её горизонтальным следом.

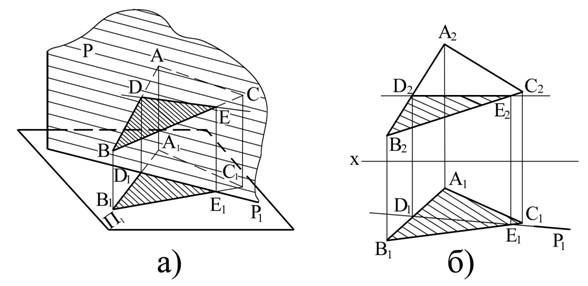
Рис. 3.6

Рассмотрим общий случай пересечения когда обе плоскости - общего положения. На рис. 3.8,а показаны две плоскости общего положения, заданные треугольником и двумя параллельными прямыми. Для определения двух общих точек линии пересечения плоскостей проводим две вспомогательные (горизонтальные) плоскости уровня R и Т. Вспомогательная плоскость R пересекает заданные плоскости по двум горизонталям h и h¹, которые в своем пересечении определяют точку 1, общую для плоскостей P и Q, так как они одновременно принадлежат вспомогательной секущей плоскости R. Вторая плоскость – посредник Т также пересекает каждую из заданных плоскостей по горизонталям h² и h³, которые параллельны первым двум горизонталям. В пересечении горизонталей получим вторую общую точку 2 заданных плоскостей. Соединяя на эпюре (рис. 3.8,б) одноименные проекции этих точек, получим проекции линии пересечения плоскостей.

Рис. 3.7

На рис. 3.9 приведены две плоскости, заданные следами. Общими точками плоскостей являются точки пересечении М и N одноименных следов. Соединяя одноименные проекции этих точек прямой линией, получил проекции линии пересечения плоскостей.

Если точки пересечения одноименных следов находятся вне поля чертежа (см. пример 5), а также в тех случаях, когда плоскости заданы не следами, а другими геометрическими элементами, то для определения линии пересечения плоскостей следует использовать вспомогательные плоскости уровня – горизонтальные или фронтальные. Необходимо отметить, что при построении линии пересечения плоскостей, заданных следами, роль вспомогательных секущих плоскостей выполняют плоскости проекций П₁ и П₂.

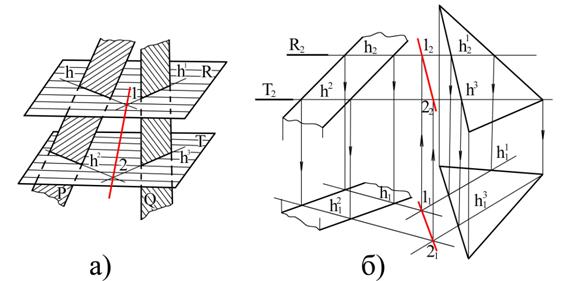
Рис 3.8

Рис. 3.9

На рис. 3.9 показан случай пересечения двух плоскостей, когда известно направление линии пресечения, т.к. плоскость Р является плоскостью уровня (Р||П₁). Поэтому достаточно иметь лишь одну точку пересечения следов и далее провести через эту точку прямую, исходя из положения плоскостей и их следов. В нашем случае линия пересечения является общей горизонталью NА плоскостей Р и Т.

Дата добавления: 2013-12-13