План лекции. Лекция 4. Криволинейный интеграл

Лекция 4. Криволинейный интеграл

4.1. Определение криволинейного интеграла по координатам

4.2. Свойства криволинейного интеграла

4.4. Вычисление криволинейного интеграла

4.4. Формула Грина-Остроградского

4.5. Независимость криволинейного интеграла от пути интегрирования

4.6. Применение криволинейного интеграла

4.1. Определение криволинейного интеграла по координатам

Векторным полем называется область пространства или плоскости, каждой точке М которой поставлен в соответствие вектор.

В пространстве проекции Р, Q, и R вектора на координатные оси являются функциями координат точки М(х, у, z): Р = Р(х, у, z); Q = (х, у, z); R = R(х, у, z), тогда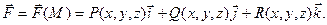

Если поле задано на плоскости, то

Пусть вдоль некоторой кривой L в поле сил

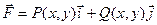
движется материальная точка. Требуется найти работу силы при перемещении материальной точки из точки А в точку В.

Рис.4.1

Решение.

1. Известно, что работа постоянной силы по перемещению материальной точки вдоль вектора 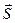равна скалярному произведению вектора на вектор 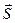, т.е.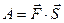

2. В общем случае сила меняется как по величине, так и по направлению, а перемеще­ние по кривой L не является прямолинейным.

Разобьем кривую L в направлении от А к В на п малых дуг точками деления А_о, А₁, А₂,..., А_п (рис. 4.1). Пусть х_k, y_k - координаты точки А_k, т.е. А_k(х_k, y_k). Впишем ломаную в кривую L, на каждой дуге A_kA_k+1 выберем произвольную точку M_k (ξ_k, η_k). Заменим кривую L ломаной А_о, А₁, А₂,..., A_k, A_k+1,..., А_п, а силу будем считать постоянной вдоль каждого звена ломаной и равной силе в точке M_k (ξ_k, η_k), т.е.

или

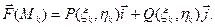(4.1)

Тогда работа силы вдоль дуги A_kA_k+1 приближенно равна работе силы (М_k) вдоль звена , т.е.

(4.2)

Проекции вектора соответственно равны Δx_k и Δy_k, т.е. (Δx_k, Δy_k), тогда скалярное произведение (2) в координатной форме имеет вид:

Отсюда приближенное значение работы А вдоль кривой L имеет вид:

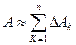
или

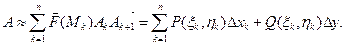(4.3)

Перейдем к пределу при условии max , получим искомое значение работы:

(4.4)

Таким образом, вычисление работы силы привело нас к нахождению предела суммы (4.3).

К пределу вида (4.4) приводят и другие задачи, поэтому отвлечемся от конкретного содер­жания рассмотренной задачи.

Пусть дана кривая L и вектор-функция 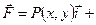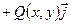, определенная в каждой точке кривой L.

Разобьем дугу АВ точками А₁,А₂,…, А_п-1 произвольным образом на малые дуги в направ­лении от А к В (см. рис. 4.1).

На каждой дуге выберем точку M_k (ξ_k,η_k) и составим скалярное произведение:

Составим сумму всех таких произведений:

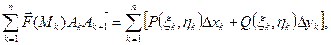(4.5)

которая называется интегральной суммой от вектор-функции

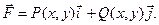
Пусть max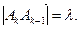

Определение. Если существует предел интегральной суммы (4.5) при условии, что, то этот предел называется криволинейным интегралом по координатам от вектор-функции 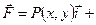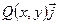вдоль кривой L (дуги АВ) в направлении от А к В и обозначается символом:

т.е.

. (4.6)

В трехмерном пространстве криволинейный интеграл имеет вид:

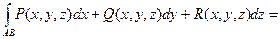
. (4.7)

Сравнивая (4.4) и (4.6) предыдущего параграфа, видим, что работа переменной силы вдоль плоской кривой АВ есть криволиней­ный интеграл от вдоль этой кривой, т.е.

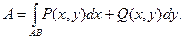
В этом и состоит механический смысл криволинейного интеграла по координатам.

Аналогично и для работы переменной силы по пространственной кривой АВ:

4.2. Свойства криволинейного интеграла

1. Знак криволинейного интеграла изменится на противоположный, если изменить на­правление интегрирования, т.е.

Так как знаки проекций дуги A_kA_k+1 на оси координат зависят от направления дуги, то и они меняют знак при перемене направления дуги.

2. Если кривую АВ (L), по которой производится интегрирование, разбить на несколько частей L₁,L₂,…,L_n, то криволинейный интеграл по кривой L будет равен сумме криволинейных интегралов по отдельным ее частям, взятых в том же направлении, т.е.

Подынтегральные выражения здесь для краткости опущены.

3. Криволинейный интеграл по замкнутой кривой L, не зависит от выбора начальной точки, а зависит только от направления обхода кривой (рис. 4.2), т.е. если А - начальная точка, то

где А₁ — любая точка кривой L, отличная от точки A.

Пусть теперь A₁ - начальная точка, тогда

Правые части последних равенств между собой равны, значит, равны и левые части.

Рис. 4.2

Таким образом,

,

т.е. криволинейный интеграл по замкнутой кривой L (по замкнутому контуру L) обозначают символом 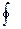. Кружок на знаке 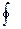интеграла служит для обозначения контура, причем положи­тельным направлением обхода контура L называют такое направление обхода, при котором дви­жение происходит против часовой стрелки. Противоположное на­правление обхода контура L называют отрицательным.

4.4. Вычисление криволинейного интеграла

Криволинейный интеграл по координатам вычисляется путем сведения его к определен­ному интегралу.

1. Пусть кривая АВ(L) задана уравнением вида у = ƒ(х), причем, если точке А соответству­ет абсцисса х = а, а точке В – абсцисса х = b,

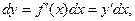
тогда криволинейный интеграл сводится к определенному интегралу:

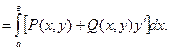
2. Пусть кривая АВ задана параметрическими уравнениями:

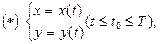
причем началу кривой - точке А соответствует t = t₀, а концу- точке В – t = T;

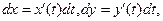
то

Таким образом, чтобы вычислить криволинейный интеграл по координатам от функции Р(х, у)dx+Q(х, у)dу по кривой (*) надо в подынтегральной функции заменить х и y, dx и dy их вы­ражениями через параметр t. За пределы интегрирования нужно взять те значения t, которым соответствуют начало и конец кривой (*).

Задача № 1. Вычислить криволинейный интеграл

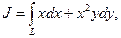
где L - отрезок прямой, соединяющей точки А(1, -2) и В(3, 1).

Решение.

1. Составим уравнения прямой АВ на плоскости:

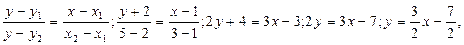
тогда

2. В качестве параметра возьмем х:

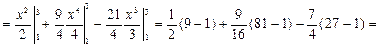
Задача № 2. Вычислить криволинейный интеграл

где L - отрезок прямой, соединяющей точки А(1,-1, 2) и В(4, 1, 3).

Решение.

1. Составим уравнение прямой АВ в проcтранстве:

2. В качестве параметра возьмем х:

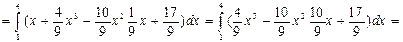
Задача №3. Вычислить криволинейный интеграл

где L - четверть окружности х²+у²=R², пробегаемая против часовой стрелки и лежащая в 1-ой четверти (рис. 4.3).

Рис. 4.3

Решение.

1. Разрешим уравнение окружности относительно у:

поэтому будем рассматривать уравнение тогда

2. В качестве параметра возьмем х и подставим значения у и dу в J, причем нижний предел интегрирования равен R, а верхний равен 0:

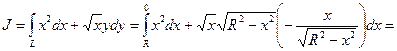
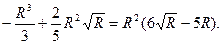
Задача № 4. Вычислить криволинейный интеграл 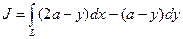вдоль первой арки циклоиды (рис. 4.4)

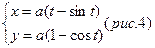
Рис.4.4

Решение.

Параметр t изменяется от 0 до 2π, 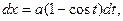Тогда

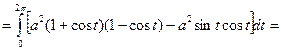
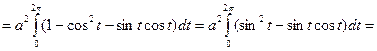
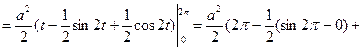
4.4. Формула Грина-Остроградского

Пусть в замкнутой плоской области D, ограниченной контуром L, определены непрерывные функции Р(х,у) и Q(х,у) имеющие непрерывные частные производные ∂Р/∂y, ∂Q/∂х, то­гда справедливо равенство:

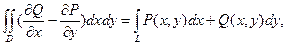(4.8)

называемое формулой Грина-Остроградского на плоскости. Она связывает двойной интеграл по области D с криволинейным интегралом по кривой L, причем контур L, который ограничивает область D, обходит ее в положительном направлении, т.е. так, что область D остается слева.

Задача № 5. Вычислить интеграл

если L - окружность х²+у² = R², используя формулу (4.8).

Решение.

Найдем ∂Р/∂у и ∂Q/∂x. По условию Р(х,у) = х-2у, Q(х,у) = 3х+у, тогда частные производные ∂ Q/ ∂ х = 3, ∂ Р/ ∂ у = -2 и они непрерывны. Следовательно, формула (8) применима, т.е.

Перейдем к полярной системе координат: х = r cos φ, y = r sin φ, (0 ≤ φ ≤ 2π), х²+у²=r², тогда уравнение данной окружности в полярной системе координат имеет вид: r = R, dxdy = rdrdφ. Таким образом,

4.5. Независимость криволинейного интеграла

от пути интегрирования

Пусть в замкнутой плоской области D, ограниченной контуром L, определены не­прерывные функции Р(х,у) и Q(х,у), имеющие непрерывные частные производные ∂Р/∂y и ∂Q/∂х. Отметим в этой области любые две точки А и В и вычислим криволинейный интеграл

(4.9)

по различным кривым, идущим из А к В, лежащим в области D. Получим, вообще говоря, различные значения данного интеграла.

Если окажется, что значение интеграла (9) по всем возможным кривым одно и то же, т.е.

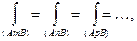
то говорят, что криволинейный интеграл не зависит от пути интегрирования в области D.

Значение интеграла в этом случае определяется заданием начальной точки А и конечно точки В.

Задача №6. Вычислить интеграл

(*)

где L – одна из линий, соединяющих точки О(0,0) и А(2,2): 1) отрезок прямой, соединяющий эти точки; 2) парабола 3) парабола 4) кубическая парабола

Решение.

1. Уравнение прямой такое: y = x, тогда dx = dy. Подставим в (*), получим:

.

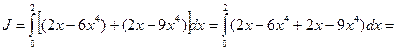
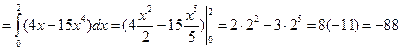2. Уравнение параболы тогда dy = xdx. Подставим в (*), получим:

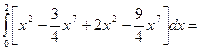
3. Уравнение параболы 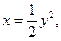тогда dx = ydy. Возьмем за параметр у. Подставим в (*), получим:

4. Уравнение кубической параболы , тогда 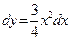. Подставим в (*), получим:

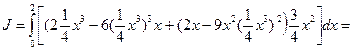
По какой бы кривой, соединяющей точки 0(0,0) и А(2,2), мы ни вычисляли интеграл (*), оказывается, что он равен одному и тому же числу.

Таким образом, величина заданного интеграла не зависит от того, по какой из указанных кривых, соединяющих эти точки, он вычисляется. Она определяется только координатами на­чальной и конечной точек этих кривых.

Необходимым и достаточным условием независимости криволинейного интеграла (4.9) от пути интегрирования является выполнение одного из следующих равносильных условий:

1.

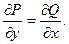
2. Криволинейный интеграл по любому замкнутому контуру L (L целиком лежит в области D) равен нулю т.е.

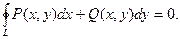
4. Подынтегральное выражение является полным дифференциалом некоторой функции U(х,у):

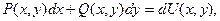
тогда имеет место формула

где С - произвольная постоянная, (х_о,у_о) - любая точка из области D. Эта формула дает возмож­ность найти множество всех функций, имеющих подынтегральное выражение своим диффренциалом. Криволинейный интеграл легко вычисляется, если взять в качестве пути интегрирования ломаную, звенья которой параллельны координатным осям. Например, ломаную, соединяющую точки М(х_о,у_о), Р(х,у_о), N(х,у) (рис. 4.8).

Рис. 4.8

Это можно сделать только в том случае, если ломаная не выходит за пределы области D.

Тогда

или

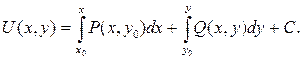
Первый интеграл справа вычисляется при постоянном у, а второй - при постоянном, хотя и произвольном, х.

Замечание. Можно было бы интегрировать и по ломаной, соединяющей точки (х_о,у_о) (хо,у) и (х,у), тогда

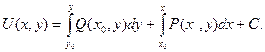
Задача №7. Найти функцию U(х,у) с помощью криволинейного интеграла от выражения:

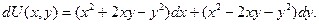
Решение.

1. Проверим, является ли заданное выражение полным дифференциалом. Здесь P(x,y) = x² +2xy - y², Q(x,y) = x² - 2xy – y², тогда

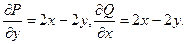
Видим, что ∂P/∂y = ∂Q/∂x. Значит, данное выражение является полным дифференциалом.

2. Вычислим криволинейный интеграл, приняв за начальную точку пути интегрирования (х_о,у_о), а за конечную (х,у):

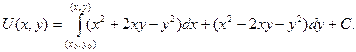
Возьмем интеграл вдоль ломаной МРN (см. рис. 4.8):

Но на отрезке МР у = у_о, dу = 0, а на отрезке РN – х = const, dx = 0, тогда

Таким образом, искомая функция

Найдем

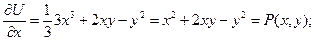
Задача решена верно.

4.6. Применение криволинейного интеграла

Работа переменной силы на криволинейном пути.

Пусть переменная сила совершает работу вдоль плоской кривой L. Непрерывные функции Р(х,у) и Q(х,у) есть проекции силы на координатные оси. Тогда работа силы на криволинейном пути L выражается криволинейным интегралом:

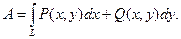
Для работы силы 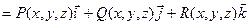по пространственной кривой L имеет место формула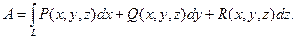

Задача № 9. Вычислить работу силы

1) по ломаной МОN: М(-4,0), N(0,2); 2) по отрезку МN.

Решение.

1) Искомая работа вычисляется следующим образом:

На отрезке МО оси Ох y = 0, следовательно, и dy = 0, а на отрезке ОN оси Оу х = 0 и dx = 0, тогда

2) Составим уравнение прямой MN в отрезках на осях:

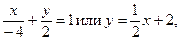тогда

Пусть х - параметр. Вычислим работу:

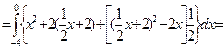
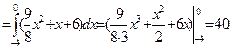
Площадь плоской области.

Пусть дана плоская область D, ограниченная замкнутым контуром L, который пересека­ется с координатными линиями не более, чем в двух точках.

С помощью криволинейного интеграла площадь плоской фигуры D вычисляется по фор­муле

причем интегрирование по контуру L производится в положительном направлении, т.е. так, чтобы область D оставалась слева.

Выражение хdу - уdx можно записать в виде определителя

Задача № 10. Вычислить площадь, ограниченную эллипсом, параметрические уравнения которого записывается так:

Решение.

Найдем dх и dу, а также подынтегральное выражение и подставим в формулу (10):

Для вычисления подынтегрального выражения воспользуемся определителем:

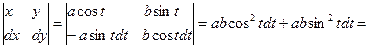
Тогда площадь эллипса равна:

(кв. ед.).

Дата добавления: 2013-12-13