Переход к пределу в неравенствах

Лекция 5. Переход к пределу в неравенствах. Ограниченность сходящихся последовательностей. Бесконечно малые последовательности.

В 1848 г. революции в Европе заставили Николая встать на путь реакции, отказаться от планов изменения положении крепостных крестьян.

Николаевская эпоха увенчалась полным провалом попыток стабилизировать самодержавие. Фактическую черту под николаевскую систему подвели смерть Николая I (в феврале 1855 г.) и поражение в Крымской войне, которая закончилась полной катастрофой для России. Крымская войны 1853-1856 гг. – этот русско-турецкая война за господство на Ближнем Востоке.

Сформулируем докажем три часто используемые свойства пределов последовательностей точек расширенной числовой прямой, связанные с равенствами и неравенствами для членов последовательностей.

1. Если для всех n=1; 2; … имеет место равенство то .

Д-во. Действительно, в этом случае для любой окрестности точки а в качестве номера , указанного в определении предела последовательности, можно взять , так как для всех n=1; 2; … имеет место включение .

2.

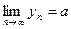Если 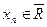, , 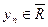, , 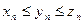n=1, 2, …, и 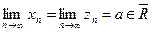, то

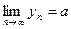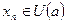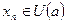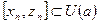Д-во. Зафиксируем произвольно окрестностьточки а. В силу условия о равенстве пределов существует такой номер n₁, что для всех номеров n>n₁ выполняется включение , и такой номер n₂,, что для всех номеров n>n₂ выполняется включение . Положим . Тогда при n>n₀ будут одновременно выполняться включения и , а следовательно, . Но в силу условия (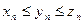) , поэтому для всех n>n₀ будет выполняться включение 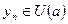, а это и означает, что

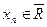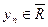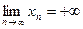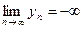Следствие. Если ,, , n=1, 2, …, и , то , а если ,то .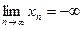

Д-во. Пусть выполнено условие 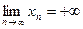. Рассмотрим вспомогательную последовательность 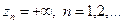Тогда, очевидно, для последовательностей { x_n }, { y_n }, { z_n } выполняются условия свойства 2 при 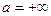, а поэтому имеет место равенство . Аналогично рассматривается и случай . ■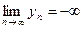

3. Если 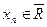, , 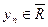n=1, 2, …,, , и 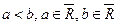, то существует такой номер n₀, что для всех номеров n>n₀ выполняется неравенство .

Д-во. Пусть и 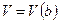- какие-либо непересекающиеся окрестности точек a b, тогда из условия a<b следует, что для любого и 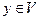выполняется неравенство x<y.

В силу условий существует номер n₀ такой,что для всех номеров n>n₀ выполняются включения . А так как x<y выполняется неравенство . ■

Следствие 1. Пусть a, b и x_n принадлежат расширенной числовой прямой. Если и a<b (a>b), то существует такой номер n₀, что для всех номеров n>n₀ выполняется неравенство x_n<b ( соответственно x_n>b).

Д-во. Пусть a<b Рассмотрим вспомогательную последовательность y_n=b. Тогда для последовательностей { x_n} и {y_n} выполняются условия свойства 3, а это означает выполнение неравенства x_n<b. Аналогично рассматривается случай a>b.■

Следствие 2. Если 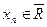, , 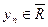n=1, 2, …,, , ,и для всех номеров n выполняется неравенство , то .

Д-во. Пусть . Если бы оказалось, что a<b, согласно свойству 3 нашелся бы такой номер n₀, что для всех n>n₀ выполнялось бы неравенство x_n<y_n, что противоречит условию. Следовательно, выполняется неравенство .■

В частности, если, n=1, 2, …,, то имеет место неравенство .

Действительно, если взять вспомогательную последовательность y_n=b, n=1, 2, …, тодля последовательностей { x_n} и {y_n} выполняются условия следствия 2, т.е. ,, и длявсехномеров n=1, 2,… выполняются неравенства 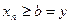. Поэтому согласно следствию 2 имеем . ■

Пример.

Дата добавления: 2013-12-13