Доказательство локальной теоремы Лапласа опускаем

Это условие обеспечивает приближенное нахождение вероятности с точностью до процента.

Функция называется функцией вероятностей (или функцией Гаусса). График функции имеет вид, изображенный на рис. 1.

Для значение функции можно взять в таблице, содержащейся во многих пособиях по теории вероятностей. Приведем небольшой фрагмент этой таблицы:

x
j(x)	0,3989	0,2420	0,0540	0,0044	0,0001	» 0

Для отрицательных значений x используют четность функции : 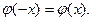Для x<- 5 и x> 5 значение На практике локальную формулу Лапласа применяют, если

(5)

Применение локальной формулы Лапласа регламентируется локальной теоремой Лапласа.

Теорема. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А в n испытаниях равно k раз, приближенно равна (тем точнее, чем больше n) значению функции.

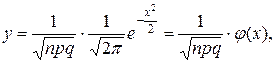при .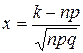

Пример 2. Монету подбрасывают 100 раз подряд. Какова вероятность того, что при этом герб выпадет ровно 40 раз?

Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда n =100 – число повторных испытаний. Будем считать событием А в каждом испытании (при каждом бросании монеты) выпадение герба. Тогда

; ; ; ; ?

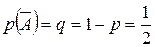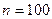Формулу Бернулли для подсчета искомой вероятности применять не будем – слишком велико число испытаний n (n =100). А так как 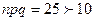, то вместо формулы Бернулли (2) применим локальную формулу Лапласа (3):

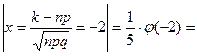
=│учтем, что 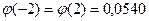│=0,0108

Другой приближенной формулой для подсчета вероятностей , применяемой при больших n, является формула Пуассона (формула редких событий):

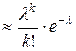, где (6)

Она применяется, когда n велико (условно n 50), а р мало (0< р <0,1), и когда npq< 10. То есть когда не оправдано ни применение формулы Бернулли, ни применение локальной формулы Лапласа. При этих условиях приближенная формула Пуассона, как и локальная формула Лапласа, обеспечивает определение искомой вероятности с погрешностью в пределах одного процента.

Кстати, так как вероятностьсобытия А мала (0< р <0,1), то при повторении испытаний событие А наступает редко. Поэтому формула Пуассона и называется формулой редких событий. Вывод этой формулы опустим.

Пример 3. Производится 50 повторных испытаний, причем вероятность появления некоторого события А в каждом из них равна 0,98. Определить вероятность того, что событие А наступит во всех 50 испытаниях.

Решение. В данной задаче

p(A)=p= 0,98; p(Ā)=q= 0,02; n= 50; k= 50;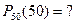

Если применить формулу Бернулли, то получим результат, который очевиден и без формулы Бернулли:

Попробуем избежать громоздкой процедуры возведения числа 0,98 в 50-ую степень (её, впрочем, можно и избежать, если использовать логарифмы). То есть заменим формулу Бернулли на локальную формулу Лапласа или Пуассона.

Так как npq =50·0,98·0,02=0,98<10, то локальную формулу Лапласа применять нельзя - мы получим слишком грубый (неточный) результат. Но и формулу Пуассона (формулу редких событий) мы тоже применить не можем, так как вероятность р не мала, а наоборот, велика. Но зато мала вероятность q непоявления этого события. В связи с этим переформулируем задачу: найдем вероятность того, что событие 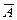появится 0 раз (ни разу). Эта вероятность, очевидно, совпадает с искомой вероятностью того, что событие А появится во всех 50 испытаниях. Тогда в этой постановке получаем:

p(Ā)=p =0,02; p(A)=q =0,98; n =50; k =0; ?

Применяя формулу Пуассона (теперь ее применять можно), получим:

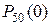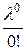
≈= | λ=np =50·0,02=1| = =≈≈ 0,37.

Рассмотрим теперь следующую задачу: какова вероятность того, что в n повторных испытаниях число k появлений события А окажется в заданных числовых пределах [ k₁; k₂ ]?

Решение этой задачи очевидно:

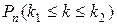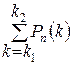=(7)

Действительно, число k окажется в пределах [ k₁; k₂ ], если оно будет равно или k₁, или k₁+1, или k₁+2, … или k₂. События, приводящие к таким значениям k, друг с другом (попарно) несовместимы. А тогда по формуле сложения вероятностей попарно несовместных событий мы и приходим к формуле (7).

Пример 4. Монета бросается 5 раз. Какова вероятность того, что при этом герб выпадет не более четырех раз?

Решение. Будем считать испытанием однократное бросание монеты. Тогда n =5-число повторных испытаний. А событием А в каждом испытании будем считать выпадение герба. Тогда:

р(A)=p =; р(Ā)=q =; n =5; 0≤ k ≤4;

Применяя формулу (7), получим:

=

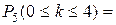
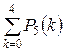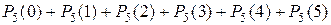
Для подсчета каждого из этих пяти слагаемых следует, очевидно, применить формулу Бернулли (2) и полученные числа сложить.

Однако эту задачу можно решить и гораздо проще - через противоположное событие:

Если число n испытаний велико, границы [ k₁; k₂ ] широкие и если, кроме того, npq >10, то вместо точной формулы (7), использование которой становится громоздким, используют приближенную интегральную формулу Лапласа:

Теорема. Если вероятность p наступления событий А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 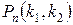того, что событие А появится в n испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу 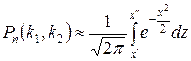, где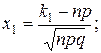

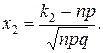
Доказательство этой теоремы мы также не будем приводить. Однако, в целях более удобного применения интегральной теоремы Лапласа, выведем формулу:

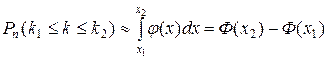(8)

Здесь:

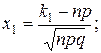
; ; (9)

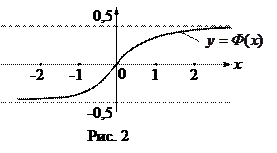Функция - это уже известная нам функция Гаусса (её график изображен на рис. 1), а функция 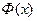называется интегралом вероятностей. График этой функции изображен на рис. 2. В любом пособии по теории вероятностей имеются таблицы значений интеграла вероятностей 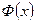, который, как и функция Гаусса, принадлежит к числу важнейших функций теории вероятностей. Эти таблицы составлены для 0≤ x ≤5. Приведем небольшой фрагмент этой таблицы:

x
Ф(x)		0,3413	0,4772	0,49865	0,499968	0,499997

Для x >5 можно считать 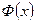=0,5. Для x <0 следует использовать нечетность функции : .

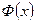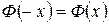Вернемся к выводу формулы (8):

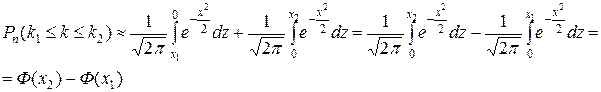
Пример 5. Монету подбрасывают 100 раз подряд. Какова вероятность того, что при этом герб выпадет от 40 до 60 раз?

Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда n =100 - число повторных испытаний. Событием А в каждом испытании будем считать выпадение герба. Тогда:

р(А)=р =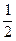; р(Ā)=q =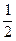; n =100; 40≤ k ≤60; =?

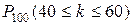Так как npq =25>10, то применим интегральную формулу Лапласа:

; ;

‌‌

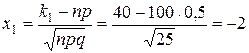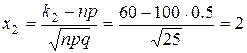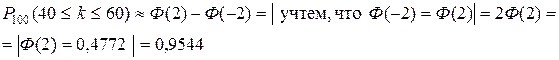
В заключении лекции выясним как вычислить вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

Задача состоит в нахождении вероятности того, что отклонение относительной частоты от постоянной вероятности p по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства

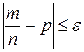. (10)

Эту вероятность будем обозначать так: . Заменим неравенство (10) ему равносильными или 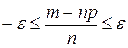. Умножая эти неравенства на положительный множитель 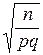, получим неравенства, равносильные исходному: . Воспользуемся интегральной теоремой Лапласа. Положим 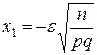и , имеем

Наконец, заменив неравенства, заключенные в скобках, равносильными им исходным неравенством, окончательно получим

. (11)

Пример 6. Вероятность того, что деталь не стандартна, p=0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности p=0,1 по абсолютной величине не более чем на 0,03.

Решение. По условию, n= 400; p= 0,1; q= 0,9; . Требуется найти вероятность 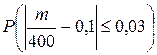. Пользуясь формулой (11), имеем .

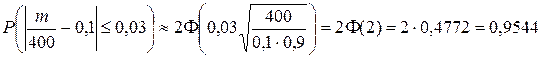Смысл полученного результата: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности p= 0,1 по абсолютной величине не более чем на 0,03.

Дата добавления: 2013-12-13