
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства математического ожидания дискретной случайной величины
|
|
|
|
Свойство 1. Математическое ожидание неизменной (постоянной) величины С равно самой этой постоянной:
М(С)=С (5)
Доказательство. Постоянная величина С принимает единственное значение (значение С) с вероятностью, равной единице. Следовательно, считая постоянную величину С частным случаем дискретной случайной величины Х, будем иметь такой закон её распределения:
| С | С |
| р | 1 |
Отсюда М(С)=С·1=С. Доказательство закончено. Отметим, что этот вывод полностью согласуется и со смыслом математического ожидания случайной величины как её среднего значения: среднее значение неизменной величины С равно ей самой.
Свойство 2. Постоянный множитель (константу) можно выносить за знак математического ожидания:
М(СХ)=С·М(Х) (6)
Доказательство. Пусть Х – дискретная случайная величина с законом распределения (1), и пусть С – любая константа. Тогда С· Х также будет дискретной случайной величиной со следующим законом распределения:
| С Х | С х1 | С х2 | … | С хn | (7) |
| р | р1 | р2 | … | рn |
Действительно, умножая случайную величину Х на множитель С, мы тем самым умножаем на С все её возможные значения (х1; х2; … хn). А вероятности значений (С х1; С х2; … С хn) величины С Х совпадают с вероятностями значений (х1; х2; … хn) величины Х, ибо величина С Х примет значение С хк (к =1, 2, … n) тогда и только тогда, когда величина Х примет значение хк (к =1, 2, … n). Но тогда из (7) следует:
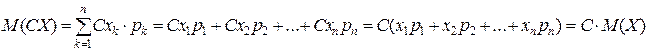 Доказательство закончено.
Доказательство закончено.
И смысл доказанного свойства (6) понятен: если изменить (увеличить или уменьшить) в С раз все возможные значения случайной величины Х, то в это же число раз изменится и её среднее значение.
Свойство 3. Математическое ожидание суммы любых двух дискретных случайных величин X и Y равно сумме их математических ожиданий:
|
|
|
М(X+Y)=M(X)+M(Y) (8)
Доказательство. Пусть
| Х | х1 | x2 | … | хn | Y | y1 | y2 | … | ym | (9) | |
| р | р1 | р2 | … | pn | q | q1 | q2 | … | qm |
- законы распределения некоторых двух дискретных случайных величин X и Y. Составим закон распределения новой случайной величины Z=X+Y – суммы величин X и Y. В качестве своих возможных значений величина Z=X+Y будет принимать все возможные суммы вида xi+yj (i=1, 2,… n; j=1, 2,… m), а вероятности этих значений, нам неизвестные, будем обозначать символами pij. Итак, закон распределения суммы Z=X+Y примет вид:
| X+Y | xi+yj | 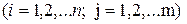 (10) (10)
|
| p | pij |
Тогда, следуя формуле (4), получаем:
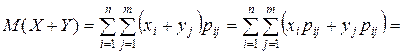
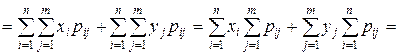 (11)
(11)
=| учтем, что 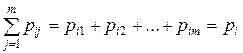 ;
; 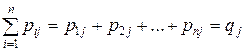 -
-
- продумайте это, опираясь на формулу 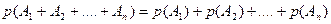 самостоятельно | =
самостоятельно | =
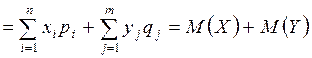
Доказательство закончено.
Из доказанного свойства (8) следует, что и математическое ожидание суммы нескольких дискретных случайных величин равно сумме их математических ожиданий. Например, для трех слагаемых получаем:
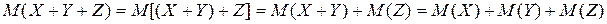 (12)
(12)
И вообще:
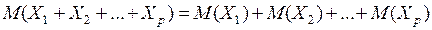 (13)
(13)
- для любых дискретных случайных величин (Х1; Х2; … Хр).
Свойство 4. Математическое ожидание разности любых двух дискретных случайных величин X и Y равно разности их математических ожиданий:
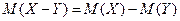 (14)
(14)
Доказательство. Оно непосредственно вытекает из уже доказанных свойств (6) и (8):

И вообще, из доказанных выше свойств вытекает, что математическое ожидание любой линейной комбинации С1Х1+С2Х2+…+СрХр любых дискретных случайных величин (Х1; Х2; … Хр), где (С1; С2; … Ср) – любые числовые множители, находится по формуле:
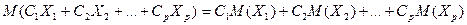 (15)
(15)
Свойство 5. Математическое ожидание произведения двух дискретных случайных величин X и Y, если эти величины независимы, равно произведению их математических ожиданий:
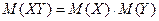 (16)
(16)
Доказательство. Пусть таблицы (9) представляют собой законы распределения двух независимых случайных величин X и Y. Их независимость означает, что в испытании эти величины принимают свои возможные значения вне всякой связи друг с другом (независимо друг от друга). Составим закон распределения дискретной случайной величины Z=XY. В качестве своих возможных значений величина Z=XY будет принимать все возможные произведения вида 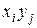
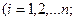
 , а вероятности
, а вероятности 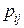 этих значений, по формуле умножения вероятностей независимых событий
этих значений, по формуле умножения вероятностей независимых событий 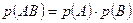 , будут равны
, будут равны  . Таким образом, закон распределения дискретной случайной величины Z=XY будет выглядеть следующим образом:
. Таким образом, закон распределения дискретной случайной величины Z=XY будет выглядеть следующим образом:
|
|
|
| XY | 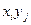
|
| p | 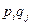
|
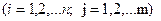 (17)
(17)
Отсюда:
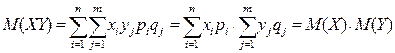 (18)
(18)
Доказательство закончено. Из доказанного свойства (16) следует, что и математическое ожидание произведения нескольких взаимно независимых случайных величин (Х1; Х2; … Хр) равно произведению их математических ожиданий:
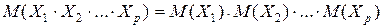 (19)
(19)
Доказательство этого проводится аналогично доказательству равенства (13).
Перейдем теперь к вопросу о том, как охарактеризовать степень разброса возможных значений (х1; х2; … хn) дискретной случайной величины Х вокруг её математического ожидания (вокруг её среднего значения) 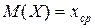 .
.
Необходимость их введения можно пояснить на примере. Пусть заданы две случайные величины 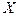 и
и 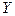 .
.
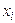
| |||||
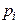
| 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
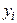
| – 10 | ||||
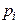
| 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
По данным из таблицы найдем математическое ожидание
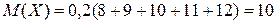 ,
,
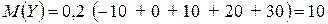 .
.
Видно, что при одной и той же величине математического ожидания, отдельные значения 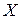 отличаются от
отличаются от 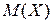 гораздо меньше, чем отдельные значения
гораздо меньше, чем отдельные значения 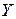 от
от 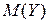 . Таким образом, становится очевидным, что одного математического ожидания недостаточно для полной характеристики случайной величины.
. Таким образом, становится очевидным, что одного математического ожидания недостаточно для полной характеристики случайной величины.
На первый взгляд может показаться, что для оценки указанного разброса следует вычислить все возможные отклонения значений случайной величины Х от её М(Х), то есть вычислить разности
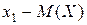 ;
;  ; ……
; …… 
и найти, с учетом вероятностей (р1; р2; … рn) этих разностей, их среднее значение. То есть найти 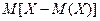 . Однако такой путь ничего не дает, так как эта величина всегда равна нулю:
. Однако такой путь ничего не дает, так как эта величина всегда равна нулю:
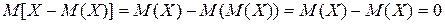 (20)
(20)
Этот результат объясняется тем, что одни возможные отклонения Х от М(Х) положительны, другие отрицательны, так что их среднее значение в результате их взаимного погашения равно нулю. Это обстоятельство указывает на целесообразность замены отклонений 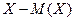 их абсолютными величинами
их абсолютными величинами 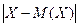 или их квадратами
или их квадратами 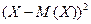 . Первый из этих вариантов предполагает оперирование с абсолютными величинами (модулями), что не очень удобно. Поэтому общепринятым является второй путь. А именно, вычисляют
. Первый из этих вариантов предполагает оперирование с абсолютными величинами (модулями), что не очень удобно. Поэтому общепринятым является второй путь. А именно, вычисляют 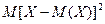 - среднее значение квадрата отклонения величины Х от её среднего значения М(Х), которое называют дисперсией
- среднее значение квадрата отклонения величины Х от её среднего значения М(Х), которое называют дисперсией 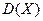 величины Х. А затем, извлекая квадратный корень из дисперсии
величины Х. А затем, извлекая квадратный корень из дисперсии 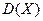 , находят среднее отклонение Х от М(Х) уже без квадрата этого отклонения. В нем знак отклонения Х от М(Х) уже не учитывается (этот знак всегда плюс).
, находят среднее отклонение Х от М(Х) уже без квадрата этого отклонения. В нем знак отклонения Х от М(Х) уже не учитывается (этот знак всегда плюс).
|
|
|
Указанный 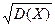 называется средним квадратическим отклонением случайной величины Х и обозначается символом σ(Х). Величина σ(Х) показывает, на сколько в среднем отклоняется Х от М(Х), если не учитывать знак отклонения Х от М(Х). Итак,
называется средним квадратическим отклонением случайной величины Х и обозначается символом σ(Х). Величина σ(Х) показывает, на сколько в среднем отклоняется Х от М(Х), если не учитывать знак отклонения Х от М(Х). Итак,
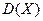 =
=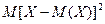 ;
;  =
=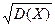 (21)
(21)
- дисперсия 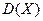 и среднее квадратическое отклонение σ(Х) величины Х.
и среднее квадратическое отклонение σ(Х) величины Х.
Обе эти величины характеризуют степень разброса значений величины Х вокруг её среднего значения М(Х).
Действительно, чем сильнее разбросаны значения Х вокруг М(Х), тем больше числовые значения 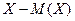 отклонений Х от М(Х). А значит, тем больше квадраты
отклонений Х от М(Х). А значит, тем больше квадраты 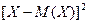 этих отклонений. Но тогда тем больше среднее значение
этих отклонений. Но тогда тем больше среднее значение 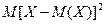 квадратов этих отклонений. То есть тем больше дисперсия
квадратов этих отклонений. То есть тем больше дисперсия 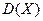 случайной величины Х. А значит, тем больше и среднее квадратическое отклонение σ(Х) величины Х. А чем меньше разброс значений случайной величины Х вокруг её математического ожидания М(Х) (то есть чем кучнее они вокруг М(Х) расположены), тем меньше величины
случайной величины Х. А значит, тем больше и среднее квадратическое отклонение σ(Х) величины Х. А чем меньше разброс значений случайной величины Х вокруг её математического ожидания М(Х) (то есть чем кучнее они вокруг М(Х) расположены), тем меньше величины 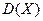 и σ(Х).
и σ(Х).
Из этих двух числовых характеристик случайной величины Х важнейшей является σ(Х) в силу её наиболее ясного смысла (σ(Х) – это среднее отклонение Х от М(Х) без учета знака этого отклонения). А дисперсия 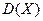 является вспомогательной величиной, по которой затем определяется среднее квадратическое отклонение σ(Х).
является вспомогательной величиной, по которой затем определяется среднее квадратическое отклонение σ(Х).
Если (1) – закон распределения дискретной случайной величины Х, то случайная величина 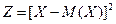 имеет, очевидно, следующий закон распределения:
имеет, очевидно, следующий закон распределения:
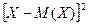
| 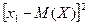
| 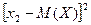
| … | 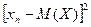
| (22) |
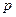
| 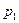
| 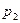
| … | 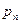
|
И тогда, согласно определению (21) дисперсии 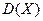 и формуле (4), получаем следующую формулу для практического подсчета дисперсии
и формуле (4), получаем следующую формулу для практического подсчета дисперсии 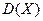 :
:
|
|
|
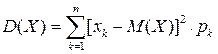 (23)
(23)
Исходя из определения дисперсии (21), для её практического вычисления можно получить и другую, так называемую упрощенную, формулу. Используя свойства математического ожидания, получим:
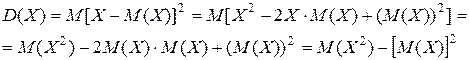 (24)
(24)
Итак,
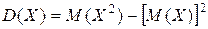 (25)
(25)
- упрощенная формула для дисперсии 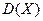 . Читается эта формула так: дисперсия дискретной случайной величины Х равна математическому ожиданию квадрата этой величины минус квадрат её математического ожидания. При этом:
. Читается эта формула так: дисперсия дискретной случайной величины Х равна математическому ожиданию квадрата этой величины минус квадрат её математического ожидания. При этом:
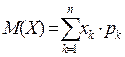 ;
; 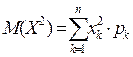 (26)
(26)
После вычисления дисперсии 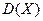 находится и σ(Х)=
находится и σ(Х)= 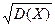 - среднее квадратическое отклонение величины Х.
- среднее квадратическое отклонение величины Х.
Для сравнения σ(Х) с М(Х) вводится величина
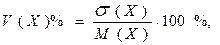
 (27)
(27)
которая называется коэффициентом вариации величины Х. Она показывает, какую долю в процентах составляет для случайной величины Х её среднее отклонение от среднего по отношению к самому среднему.
Пример 6. дискретная случайная величина Х имеет следующий закон распределения:
| Х | 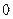
| 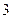
| 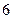
|
| p | 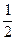
| 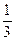
| 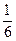
|
Найти её числовые характеристики М(Х); D(Х); σ(Х); V(X)%.
Решение.
1) Найдем М(Х). Используя формулу (4), получим:
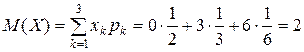 .
.
2) Найдем D(Х). Используя основную формулу (1.23), получаем:
D(Х) =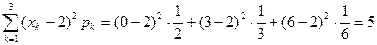 ;
;
Заметим, что то же самое значение D(Х)= 5мы получим, если используем упрощенную формулу (25) и выражения (26):
M(X)= ; M(X2) =
; M(X2) = ; D(Х) =
; D(Х) =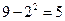
3) Найдем σ(Х):
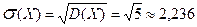 .
.
4) Найдем V(X)%:
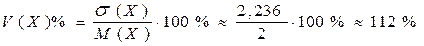 .
.
Таким образом, среднее значение x ср данной случайной величины Х равно М(Х)= 2. То есть принимая три возможных значениях (0; 3; 6), случайная величина Х в среднем принимает значение 2. Найденное значение не совпадает со средним арифметическим этих чисел (с 3) и оказалось ближе к 0, нежели к 6. Это произошло потому, что вероятность  значения 0 гораздо больше вероятности
значения 0 гораздо больше вероятности  значения 6. А это значит, что при повторных испытаниях значение 0 будет встречаться гораздо чаще (втрое чаще), чем значение 6. Поэтому и среднее из значений, принимаемых случайной величиной Х, будет сдвинуто от среднего арифметического (от числа 3) в сторону нуля. Точно так же средний балл аттестата зрелости выпускника школы ближе к трем, чем к пяти, если в этом аттестате больше троек, чем пятерок.
значения 6. А это значит, что при повторных испытаниях значение 0 будет встречаться гораздо чаще (втрое чаще), чем значение 6. Поэтому и среднее из значений, принимаемых случайной величиной Х, будет сдвинуто от среднего арифметического (от числа 3) в сторону нуля. Точно так же средний балл аттестата зрелости выпускника школы ближе к трем, чем к пяти, если в этом аттестате больше троек, чем пятерок.
Далее, среднее отклонение σ(Х) величины Х от её среднего значения М(Х)= 2 оказалось равным ≈2,236. И это тоже хорошо объяснимо. Действительно, у случайной величины Х три возможных значения (0; 3; 6) при хср=М(Х)= 2. Отклонения этих значений от их среднего значения хср =2 составляют (без учета знака отклонения) соответственно (2; 1; 4). Из этих трех отклонений средним оказалось σ(Х)≈ 2,236. Оно наиболее близко к 2, то есть наиболее близко к отклонению значения 0 от хср =2. И это оправдано, так как значение 0 величины Х при повторных испытаниях будет встречаться чаще других значений.
Наконец, величина коэффициента вариации величины Х показывает, что σ(Х)≈ 2,236 (среднее отклонение от среднего) по отношению к М(Х)= 2 (к самому среднему) составляет ≈112%.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1272; Нарушение авторских прав?; Мы поможем в написании вашей работы!