Лекция 59. Виды распределений непрерывных случайных величин

1. Равномерное распределение.

Определение. Непрерывная случайная величина Х называется распределенной равномерно, если все ее возможные значения равновероятны.

Это значит, что если Х - равномерно распределенная случайная величина, и – промежуток ее возможных значений, то плотность вероятности f(x) величины Х для всех одинакова:

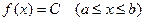. (1)

Константа С не может быть произвольной. Ее значение должно быть таким, чтобы обеспечивалось условие . Из него следует:

(2)

Таким образом, равномерно распределенная на отрезке непрерывная случайная величина Х имеет на нем следующую плотность вероятности (рис. 1):

(3)

А числовые характеристики этой величины таковы:

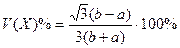(4)

Получим

Равномерно распределенными будут, например, следующие величины:

1) Координата Х точки, бросаемой наудачу на отрезок ;

2) Ошибка Х, производимая при округлении приближенных чисел до нужного десятичного знака при производстве арифметических вычислений;

3) Время Т ожидания пассажиром троллейбуса, маршрутного такси, поезда метро и прочих средств общественного транспорта при регулярном графике их движения. И т.д.

Пример 1. При производстве арифметических вычислений их результаты округляют до сотых. Какова вероятность того, что ошибка Х, допущенная при округлении очередного числа, окажется не больше одной тысячной (без учета ее знака)?

Решение. Ошибка Х округления чисел до сотых – равномерно распределенная случайная величина, принимающая свои возможные значения (если не учитывать их знак) на промежутке [0; 0,005]. Поэтому ее плотность вероятности, согласно (3), будет иметь вид:

.

А тогда, используя формулу (3.6), получим и искомую вероятность:

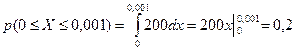
2. Нормальное распределение.

Пусть случайная величина Х может быть представлена в виде:

(5)

Здесь - некоторая константа, а - сумма очень большого (бесконечно большого) числа независимых случайных величин Х_к, влияние каждой из которых на всю эту сумму ничтожно мало.

Примерно такая ситуация, в частности, сложится, если Х – результат измерения некоторым прибором некоторой величины (например, Х – результат взвешивания на весах некоторой массы ). Действительно, результат Х измерения не обязательно совпадет с истинным значением измеряемой величины, ибо к этому истинному значению добавляются ошибки Х_k, вносимые:

а) прибором; б) измерителем; в) внешней средой.

Такого рода помех измерению в принципе бесконечно много, и каждая из них вносит свою ошибку Х_k в результат Х измерения.

Если бы ошибок Х_k не было (а значит, не было бы помех измерению), то результат измерения Х совпал бы с - с истинным значением измеряемой величины. И, таким образом, он не был бы случайной величиной. Но от окружающей среды защититься полностью невозможно. А потому ошибки Х_k измерения, вызываемые помехами, неизбежны при любом измерении. Все эти ошибки Х_k, вообще говоря, мелкие. Но их очень много, ибо очень много внешних факторов, влияющих на процесс измерения. Действуют эти факторы, как правило, независимо друг от друга. Поэтому результат Х измерения –случайная величина, которая в итоге и принимает вид (5).

Будем считать, что среди ошибок измерения нет ошибок систематических. То есть нет ошибок, приводящих к систематическому завышению или занижению результатов измерения (из-за неотрегулированности прибора, недобросовестности измерителя, и т.д.). То есть все ошибки Х_к связаны исключительно со случайными помехами измерению. Тогда величина Х (результат измерения) с одинаковой вероятностью может оказаться как больше , так и меньше . При этом, в соответствии с формулой (5), она теоретически может принять значение х, как угодно далеко отстоящее от в ту или другую сторону. Но чем дальше оно будет отстоять от , тем менее вероятным оно будет. Действительно, большое отклонение х от - это большая итоговая ошибка измерения. А большие ошибки измерения, естественно, менее вероятны, чем малые. Очень же большие ошибки практически невероятны.

Из всего сказанного выше вытекает, что случайная величина Х, имеющая структуру (5)– это непрерывная случайная величина, возможные значения которой заполняют всю числовую ось ох. А её плотность вероятности имеет в принципе графический вид, изображенный на рис. 2.

Российский математик Ляпунов в начале 20-го века вывел аналитический вид (формулу) для этой плотности вероятности:

(6)

Здесь - мода и одновременно математическое ожидание (среднее значение) величины Х, а 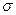– ее среднее квадратическое отклонение (среднее отклонение Х от без учета знака отклонения). То есть

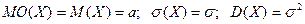(7)

Если Х – результат измерения величины , то в формулах (7) - это истинное значение измеряемой величины (обычно неизвестное и подлежащее определению), а 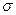– среднее значение итоговой (суммарной) ошибки измерения, зависящее как от точности измерительного прибора, так и от условий измерения. Эта ошибка обычно определяется опытным путем.

Случайная величина Х, представимая в виде (5), называется распределенной нормально. То есть такая величина Х имеет нормальное распределение. Или, что то же самое, величина Х распределена по нормальному закону.

Нормально распределенная случайная величина Х может в принципе принять любое значение от 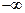до 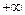, а ее плотность вероятности имеет вид (6).

Результаты различного рода измерений – это случайные величины, распределенные приблизительно по нормальному закону. Приблизительно нормально распределенными случайными величинами будут и итоговые (суммарные) ошибки этих измерений, ибо они имеют вид (5) при =0. И вообще, приблизительно нормально распределенными будут все случайные величины Х, которые имели бы в каждом испытании неизменное значение , если бы не незначительные случайные добавки, которых много и которые “уводят” значение величины Х от в большую или в меньшую сторону.

Например, если станок-автомат настроен на изготовление деталей определенного размера , то реальный размер Х изготавливаемых деталей, в силу различного рода случайных факторов, будет иметь вид (5) и, следовательно, будет случайной величиной, распределенной приблизительно нормально.

Приблизительно нормально распределенными случайными величинами можно также считать суточный привес одного или группы животных при постоянном рационе их кормления; суточный надой одной или нескольких коров при одних и тех же условиях их содержания; расход семян на единицу засеваемой площади при неизменной технологии сева; ежедневный объем продаж магазина при неизменном в целом спросе на продукцию этого магазина, и т.д. С такого рода случайными величинами чаще всего приходится иметь дело на практике. Отсюда возник и термин для их названия – “нормально распределенные”.

Нормально распределенные случайные величины обладают важным свойством: если Х – нормально распределенная величина с некоторыми параметрами (;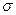), то любая линейная комбинация - тоже нормально распределенная случайная величина, имеющая параметры (). В частности, нормально распределенная случайная величина

(8)

имеет параметры () и называется нормированной нормально распределенной случайной величиной. Ее плотность вероятности , согласно (6), имеет вид

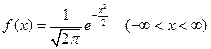(9)

То есть она представляет собой функцию Гаусса.

Вид графика плотности вероятности нормально распределенных случайных величин Х, согласно рис.2, зависит от величины их параметров (). А именно, значение определяет вертикальную ось симметрии этого графика, а величина 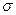определяет высоту графика: чем 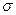меньше, тем вершина графика выше. А чем график выше, тем он уже. Сужение графика плотности вероятности с увеличением его высоты связано с тем, что площадь между осью ох и графиком плотности вероятности для любой непрерывной случайной величины, согласно свойству плотности вероятности, должна быть равна единице. Поэтому если этот график увеличивает свою высоту, то он автоматически становится уже (рис.3):

Рассмотрим теперь следующий важный для практики вопрос: какова вероятность того, что в результате испытания нормально распределенная случайная величина Х с параметрами (; 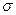) примет значение в некотором заданном числовом промежутке ? Ответ на этот вопрос мы получим с помощью формулы , которая приводит к следующему результату:

(10)

Здесь – функция Лапласа. Действительно,

На основании полученной формулы (10) следует (выведите это самостоятельно), что для любого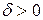

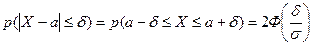(11)

Геометрическая иллюстрация последнего равенства дана на рис.4.

В частности, используя формулу (11) и таблицу функции , получим:

(12)

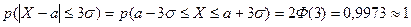
Последний из этих результатов означает, что практически наверняка экспериментальное значение нормально распределенной случайной величины Х будет содержаться в пределах . То есть событие, состоящее в том, что экспериментальное значение нормально распределенной случайной величины Х отклонится от её среднего значения в ту или другую сторону больше, чем на (на три средних отклонения от среднего), практически невероятно. Этот вывод называют правилом трех сигм.

Например, если Х – результат взвешивания некоторой массы , то представляет собой среднюю ошибку взвешивания на данных весах. И если, например, 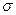= 5 г, то в соответствии с правилом трех сигм практически невероятно, что случайная ошибка взвешивания окажется больше 15 г (в ту или в другую сторону).

Пример 2. Станок-автомат изготавливает шарики. Шарик считается годным, если отклонение Х – диаметра шарика от проектного размера по абсолютной величине не превосходит 0,7 мм. Опытным путем установлено, что 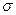==0,4 мм. Определить, сколько процентов годных шариков изготовляет автомат.

Решение. Отклонение Х диаметра шарика от проектного размера – это ошибка диаметра шарика. При условии, что станок настроен правильно (систематических ошибок в работе станка нет), эта ошибка Х складывается из множества мелких случайных ошибок Х_к, связанных с действием различных независимых друг от друга случайных факторов. То есть . Таким образом, ее выражение соответствует формуле (5) при = 0. А значит, Х – случайная величина, распределенная нормально с математическим ожиданием (средним значением) = 0 и средним квадратическим отклонением 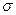= 0,4 мм(дано по условию задачи). Величина 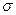= 0,4 мм означает, что среднее значение отклонения ошибки Х от ее среднего значения = 0 без учета знака отклонения, то есть среднее значение самой этой ошибки, если не учитывать ее знак, составляет 0,4 мм. Иначе говоря, станок работает со средней ошибкой 0,4 мм(в ту или другую сторону).

По условию задачи, каждый изготовленный станком-автоматом шарик будет считаться годным, если ошибка Х его диаметра будет удовлетворять неравенству 0,7 мм, то есть она будет в пределах [-0,7 мм; 0,7 мм]. Найдем вероятность этого. Применяя формулу (11), получаем:

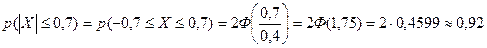
Итак, вероятность того, что каждый изготовленный станком-автоматом шарик окажется годным, составляет 0,92. Это значит, что этот станок изготовляет в среднем 92% годных шариков.

3. Распределение (хи-квадрат).

Пусть – независимые нормированные нормально распределенные случайные величины (то есть у каждой из них = 0 и ). Тогда сумма квадратов этих величин

(13)

является случайной величиной, распределенной по закону (хи-квадрат) с степенями свободы. Понятие «число степеней свободы» заимствовано из физики, где под ним понимается число независимых координат, определяющих положение тел в процессе их движения. В частности, при движении по прямой точка обладает одной степенью свободы; при свободном движении по плоскости – двумя степенями свободы; при свободном движении в пространстве – тремя степенями свободы. Если же движение точки несвободно – например, она может двигаться по плоскости лишь вдоль какой-то линии 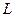с уравнением , то ее положение на плоскости полностью определяется лишь одной координатой х, ибо другая координата y уже не является независимой, так как выражается через х. В этом случае у движущейся по плоскости точки будет не две, а одна степень свободы. И так далее. Возвращаясь к выражению (13) для случайной величины , видим, что в ее образовании участвуют независимых величин . Поэтому у нее и степеней свободы.

Очевидно, что величина может принимать лишь неотрицательные значения . Доказано, что плотность вероятности случайной величины с степенями свободы имеет вид

(14)

где - быстро убывающие с номером числовые коэффициенты, выражения которых ввиду их сложности не приводим. При этом график плотности вероятности для =1, =2 и >2 в принципе имеет вид:

Также доказано, что

(15)

С увеличением числа степеней свободы распределение медленно приближается к нормальному.

4. Показательное распределение. Функция надежности.

Пусть некоторый природный или искусственный объект начинает функционировать в момент времени t= 0. В качестве такого объекта можно, например, рассматривать живое существо с момента его рождения или с любого другого этапного для него момента; работающий механизм или элемент этого механизма с момента его включения, и т.д.

Пусть Т – время безаварийного функционирования этого объекта (для живого существа это может быть время до утраты пригодности его к тому или иному виду деятельности или до его смерти; для механизма это может быть время до первой его поломки или до окончательного выхода его из строя, и т.д.). Согласно своего смысла, Т – непрерывная случайная величина, возможные значения t которой могут быть, в принципе, любыми неотрицательными числами: .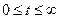

Поставим теперь естественный вопрос: какова вероятность того, что для данного объекта будет иметь место неравенство 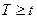, где t – некоторое заданное время? То есть поставим вопрос: какова вероятность того, что за время t функционирующий объект не выйдет из строя? Вероятность эту обозначим символом R(t) и назовем функцией надежности:

(22)

Очевидно, что для любого функционирующего объекта указанная вероятность R(t) сохранения своей работоспособности в течение времени t будет убывать с возрастанием t, начиная с 1 при t= 0,и стремиться к нулю при 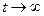. Более того, как показали многочисленные практические исследования самых разнообразных объектов (технических устройств; природных образований; живых организмов и т.д.) это убывание функции надежности R(t) осуществляется приблизительно по показательному (экспоненциальному) закону

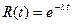
(23)

Такое поведение функции надежности R(t) называют еще показательным законом надежности (рис. 6).

Выясним смысл параметра в случае показательного закона надежности. Для этого найдем плотность вероятности и основные числовые характеристики () случайной величины Т.

Начнем с нахождения . Ее будем искать, исходя из определения плотности вероятности непрерывной случайной величины.

Пусть t – некоторое фиксированное значение величины Т (t – момент выхода объекта из строя). Окружим это значение некоторым частичным промежутком [] длиной и рассмотрим вероятность того, что случайная величина Т примет значение внутри этого промежутка. То есть рассмотрим вероятность того, что объект выйдет из строя в какой-то момент времени, принадлежащий этому промежутку (рис. 7).

t

Согласно смысла функции надежности, R(t₁) и R(t₂) – это вероятности того, что объект выйдет из строя после моментов времени t₁ и t₂ соответственно (рис. 8). Вероятность R(t₁) больше вероятности R(t₂) на , откуда следует:

(24)

Тогда по определению плотности вероятности получаем:

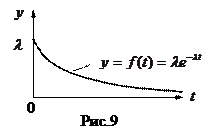
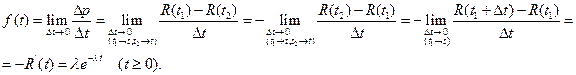
Итак,

(25)

– плотность вероятности случайной величины Т, представляющей собой время безаварийного функционирования объекта, имеющего показательный закон надежности. График этой плотности вероятности изображен на рис.9. Кстати, распределение указанной случайной величины Т носит название показательного распределения.

Зная плотность вероятности , можем теперь найти и числовые характеристики () случайной величины Т:

;

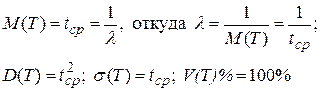(26)

Здесь t_ср – среднеевремя безаварийного функционирования объекта. Через t_ср можно выразить и функцию надежности (23) случайной величины Т, и плотность ее вероятности (25):

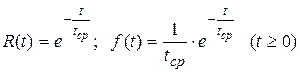(27)

В заключение отметим следующий важный факт: вероятность безаварийной работы любого объекта на интервале времени длительности t, если время Т безаварийной работы этого объекта имеет показательное распределение, не зависит от начала рассматриваемого интервала, а зависит только от его длительности t.

Для доказательства этого утверждения введем следующие события (рис. 10):

А – безотказное функционирование объекта на интервале времени ();

В – безотказное функционирование объекта на интервале времени ();

С – безотказное функционирование объекта на интервале времени ():

Очевидно, что С=АВ, откуда следует:

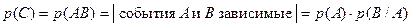(28)

Таким образом

(29)

где R(t) – вероятность безотказного функционирования объекта на интервале времени (), а 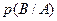– вероятность безотказного функционирования объекта на интервале времени (). Эти вероятности равны, что и доказывает заявленный выше факт.

Отметим, что случайные величины, имеющие показательное распределение (показательный закон надежности), тесно связаны с событиями простейшего (пуассоновского) потока. Действительно, вероятность того, что за время t не появится ни одного из событий простейшего потока, найдется по формуле:

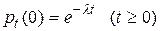(30)

Здесь - интенсивность пуассоновского потока (среднее число событий потока, появляющихся за единицу времени). Тогда – среднее время, проходящее между появлениями отдельных событий потока. С учетом этого вероятность (30) примет вид:

(4.31)

Но точно такой же вид, согласно (27), имеет показательная функция надежности R(t), определяющая вероятность безаварийной работы объекта в течение времени t. Таким образом, время Т безаварийной работы объекта при показательном законе надежности и время Т, проходящее между соседними событиями простейшего потока, имеют одно и то же распределение. А именно, показательное распределение с плотностью вероятности , описываемой формулой (27).

Пример 3. Среднее время безотказной работы некоторого устройства, имеющего показательный закон надежности, равно 50 часам. Определить вероятность того, что устройство безотказно проработает 100 часов.

Решение. Пусть Т – время безотказной работы устройства. Так как среднее значение этого времени t_ср= 50 часам, то функция надежности R(t) для рассматриваемого устройства имеет, согласно (27), вид:

(t – в часах, t≥ 0)

Тогда, согласно (22), получаем искомую вероятность:

Дата добавления: 2013-12-13