
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Различают три основных типа краевых задач математической физики
Основные понятия теории уравнений математической физики
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
10. Уравнение
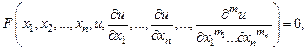 (1)
(1)
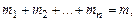
где u - искомая функция,  - независимые переменные, F – известная функция своих аргументов, называется дифференциальным уравнением в частных производных. Наивысший порядок частных производных, входящих в уравнение (1), называется порядком этого уравнения. Решением уравнения (1) в некоторой области D называется любая функция
- независимые переменные, F – известная функция своих аргументов, называется дифференциальным уравнением в частных производных. Наивысший порядок частных производных, входящих в уравнение (1), называется порядком этого уравнения. Решением уравнения (1) в некоторой области D называется любая функция  , необходимое число раз дифференцируемая и обращающая его в тождество.
, необходимое число раз дифференцируемая и обращающая его в тождество.
Пример 1. Решить уравнение 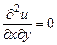 , где
, где  .
.
Решение. Исходное уравнение можно записать в виде  , значит, производная
, значит, производная 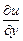 зависит только от y, т.е.
зависит только от y, т.е.  , где
, где 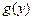 – произвольная дифференцируемая функция. Отсюда
– произвольная дифференцируемая функция. Отсюда  , где
, где  – произвольная дифференцируемая функция, зависящая только от x, а
– произвольная дифференцируемая функция, зависящая только от x, а  . Таким образом, решением рассматриваемого уравнения является любая функция вида
. Таким образом, решением рассматриваемого уравнения является любая функция вида 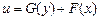 , где
, где  и
и  – произвольные дифференцируемые функции.□
– произвольные дифференцируемые функции.□
Пример 2. Найти решение уравнения 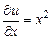 , удовлетворяющее условию
, удовлетворяющее условию 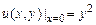 .
.
Решение. Общее решение данного уравнения имеет вид 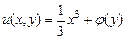 . Подставим в полученное выражение
. Подставим в полученное выражение  , будем иметь
, будем иметь  . Отсюда
. Отсюда 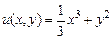 . □
. □
20. Классификация линейных уравнений второго порядка. Рассмотрим уравнение
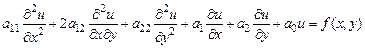 , (3)
, (3)
I. Пусть в уравнении (3)  – постоянные коэффициенты. Для того, чтобы привести уравнение (3) к каноническому виду применяют способ характеристик: составляется уравнение
– постоянные коэффициенты. Для того, чтобы привести уравнение (3) к каноническому виду применяют способ характеристик: составляется уравнение
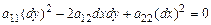 , (4)
, (4)
так называемое уравнение характеристик, которое распадается на два уравнения. Разделим уравнение (4) на 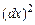 и произведем замену
и произведем замену 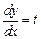 , тогда уравнение (4) примет вид
, тогда уравнение (4) примет вид
 . (5)
. (5)
1) Если  , то уравнение эллиптического типа. Для этого уравнения интегралы уравнения характеристик имеют вид
, то уравнение эллиптического типа. Для этого уравнения интегралы уравнения характеристик имеют вид  , где
, где  и
и 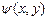 – действительные функции. С помощью подстановки
– действительные функции. С помощью подстановки 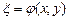 ,
, 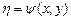 уравнение (3) приводится к каноническому виду
уравнение (3) приводится к каноническому виду
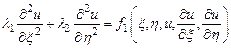 ,
,
где 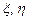 – новые переменные;
– новые переменные;  – известная функция.
– известная функция.
2) Если  , то уравнение гиперболического типа. Тогда уравнение характеристик имеет два интеграла:
, то уравнение гиперболического типа. Тогда уравнение характеристик имеет два интеграла: 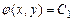 ,
,  . С помощью замены переменных
. С помощью замены переменных 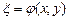 ,
, 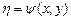 дифференциальное уравнение (3) приводится к каноническому уравнению вида
дифференциальное уравнение (3) приводится к каноническому уравнению вида 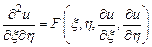 .
.
3) Если  , то уравнение параболического типа. Тогда уравнение характеристик дает лишь один интеграл
, то уравнение параболического типа. Тогда уравнение характеристик дает лишь один интеграл  . В этом случае замена переменных
. В этом случае замена переменных 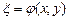 ,
, 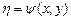 , где
, где 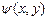 – некоторая функция, для которой
– некоторая функция, для которой 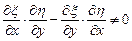 . Тогда уравнение приводится к каноническому виду
. Тогда уравнение приводится к каноническому виду 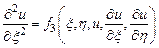 или
или 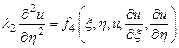 , где
, где 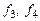 – известные функции.
– известные функции.
После указанных подстановок будем иметь уравнение
 , (5)
, (5)
где
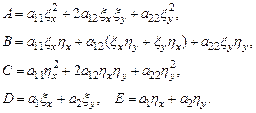
Можно заметить, что для уравнений: 1) эллиптического типа  , 2) гиперболического типа
, 2) гиперболического типа 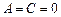 , 3) параболического типа
, 3) параболического типа 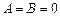 или
или  .
.
II. Если в уравнении (3) коэффициенты  переменные, то для него выделяются области эллиптичности, гиперболичности и параболичности.
переменные, то для него выделяются области эллиптичности, гиперболичности и параболичности.
Пример 3. Привести к каноническому виду дифференциальное уравнение
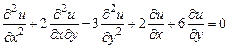 .
.
Решение. В данном случае  ,
,  ,
,  . Так как
. Так как 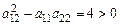 , то данное уравнение является уравнением гиперболического типа. Составим уравнение характеристик:
, то данное уравнение является уравнением гиперболического типа. Составим уравнение характеристик: 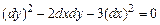 . Оно распадается на два:
. Оно распадается на два:  ,
, 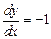 . Интегрируя их, соответственно получаем:
. Интегрируя их, соответственно получаем:  ,
, 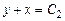 . Вводим новые переменные по формулам
. Вводим новые переменные по формулам 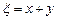 ,
,  .
.
Вычислив 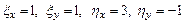 , получим:
, получим: 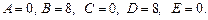
Подставив коэффициенты в уравнение (5), получим  . □
. □
Пример 4. Привести к каноническому виду уравнение  .
.
Решение. Здесь  ,
,  ,
,  ,
,  , т.е. имеем уравнение эллиптического вида. Уравнение характеристик запишется в виде:
, т.е. имеем уравнение эллиптического вида. Уравнение характеристик запишется в виде: 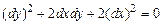 , получаем два семейства мнимых характеристик:
, получаем два семейства мнимых характеристик:  и
и  . Производя замену переменных
. Производя замену переменных 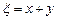 ,
,  , имеем
, имеем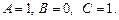 Подставив найденные значения в (5), получим
Подставив найденные значения в (5), получим  . □
. □
30. Постановка задач для уравнений математической физики. В отличие от обыкновенных дифференциальных уравнений, для которых общее решение выражается через определенные функции, в случае уравнений в частных производных вид функций, через которые выражается их решение, не конкретизирован (с помощью одних только уравнений эти функции найти нельзя).
Для того, чтобы из бесчисленного множества решений дифференциального уравнения выделить частное решение, описывающее конкретный физический процесс, необходимо задать дополнительные условия. Обычно эти условия следуют из физической постановки задачи и физического смысла искомой функции. Чаще всего такими дополнительными условиями являются начальные условия (если искомая функция зависит от времени) и граничные (или краевые) условия. Начальные условия задают значение функции и определенного числа ее производных в начальный момент времени 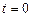 .
.
1. Задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия; область G, где происходит процесс, описываемый дифференциальным уравнением, есть пространство  ; граничные условия отсутствуют.
; граничные условия отсутствуют.
2. Краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области G; начальные условия отсутствуют.
3. Смешанная задача для уравнений гиперболического и параболического типов: задаются и начальные, и граничные условия, 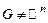 .
.
§ 2. Основные уравнения математической физики
10. Уравнение колебания струны. Постановка задачи. Струна длиной l натянута с силой  и находится в прямолинейном положении равновесия,
и находится в прямолинейном положении равновесия, 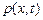 – непрерывная линейная плотность внешних сил,
– непрерывная линейная плотность внешних сил, 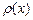 – непрерывная линейная плотность струны. В момент времени
– непрерывная линейная плотность струны. В момент времени 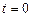 точкам струны сообщаются начальные отклонения и скорости. Вывести уравнение малых поперечных колебаний струны при
точкам струны сообщаются начальные отклонения и скорости. Вывести уравнение малых поперечных колебаний струны при 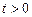 , если концы струны
, если концы струны
а) закреплены жестко;
б) свободны, т.е. могут свободно перемещаться по прямым, параллельным направлению отклонения u;
в) двигаются в поперечном направлении по заданным законам.
Сопротивлением среды и действием силы тяжести пренебречь.
Решение. Струной называется тонкая нить, которая может свободно изгибаться. Пусть струна в плоскости 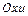 осуществляет поперечные колебания около своего положения равновесия, которое совпадает с осью
осуществляет поперечные колебания около своего положения равновесия, которое совпадает с осью 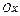 . Величину отклонения струны от положения равновесия в момент времени
. Величину отклонения струны от положения равновесия в момент времени 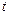 обозначим через
обозначим через  . Рассматриваются только малые колебания струны. Тогда при постоянной плотности
. Рассматриваются только малые колебания струны. Тогда при постоянной плотности 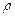 функция
функция  удовлетворяет дифференциальному уравнению.
удовлетворяет дифференциальному уравнению.
Уравнение вынужденных колебаний струны, если 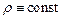 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид
 ,
,
где  – постоянная,
– постоянная,  – сила начального натяжения струны,
– сила начального натяжения струны, 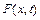 – непрерывная линейная плотность внешних сил.
– непрерывная линейная плотность внешних сил.
Кроме того, функция 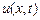 удовлетворяет начальным условиям
удовлетворяет начальным условиям
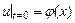 ,
, 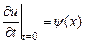 , где
, где 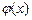 ,
,  – заданные функции.
– заданные функции.
Приведем краевые условия:
а) Если концы струны жестко закреплены, то  ,
, 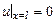 .
.
б) В случае свободных концов имеют место условия 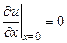 ,
,  .
.
в)  ,
,  , где функции
, где функции  определяют закон движения концов струны
определяют закон движения концов струны 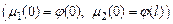 .
.
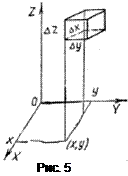
Пример 1. Задача о колебаниях мембраны (свободно изгибающейся натянутой пленки), занимающей в положении равновесия некоторую область D в плоскости Oxy, ограниченную замкнутой кривой L. Рассмотреть только малые поперечные колебания мембраны в предположении, что она находится под действием равномерного натяжения T, приложенного к краям мембраны.Величину смещения точки  мембраны от положения равновесия в момент времени
мембраны от положения равновесия в момент времени 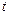 обозначим через
обозначим через  . Тогда функция
. Тогда функция  удовлетворяет уравнению
удовлетворяет уравнению
Дифференциальное уравнение поперечных колебаний мембраны в случае однородной мембраны  , уравнение малых колебаний мембраны можно записать в виде
, уравнение малых колебаний мембраны можно записать в виде
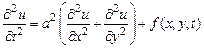 , (7)
, (7)
где 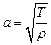 ,
, 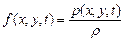 . где
. где 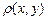 – поверхностная плотность мембраны,
– поверхностная плотность мембраны, 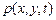 -- внешняя сила
-- внешняя сила
Если внешняя сила отсутствует, т.е.  , то из (7) получаем уравнение свободных колебаний однородной мембраны
, то из (7) получаем уравнение свободных колебаний однородной мембраны
 .
.
Как и при рассмотрении колебаний струны, для полного определения движения мембраны нужно задать в начальный момент времени 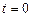 смещение и скорость всех точек мембраны:
смещение и скорость всех точек мембраны:
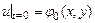 ,
, 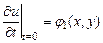 .
.
 Далее, так как на контуре L мембрана закреплена, то должно быть
Далее, так как на контуре L мембрана закреплена, то должно быть 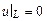 при любом
при любом 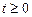 . □
. □
Уравнение теплопроводности. Рассмотрим в 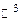 с декартовой системой координат OXYZ твердое тело V. Пусть температура этого тела в любой точке
с декартовой системой координат OXYZ твердое тело V. Пусть температура этого тела в любой точке 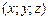 в момент времени t определяется функцией
в момент времени t определяется функцией  . Тогда производные
. Тогда производные 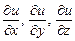 характеризуют скорость изменения температуры в момент времени t в направлении осей X, Y и Z соответственно. Тело V предполагается изотропным, т.е. его тепловые свойства не зависят от направления. Известно, что теплота переходит из более нагретых мест в менее нагретые. Обозначим
характеризуют скорость изменения температуры в момент времени t в направлении осей X, Y и Z соответственно. Тело V предполагается изотропным, т.е. его тепловые свойства не зависят от направления. Известно, что теплота переходит из более нагретых мест в менее нагретые. Обозначим  коэффициент теплопроводности тела, а c – его удельную теплоемкость.
коэффициент теплопроводности тела, а c – его удельную теплоемкость.
Уравнение теплопроводности тела:
 . (9)
. (9)
где 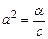 .
.
Уравнение (9) получено в предположении, что внутри тела отсутствуют тепловые источники. Если же плотность тепловых источников (количество поглощенной или выделенной теплоты за единицу времени в единице объема тела) в теле V равна 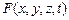 , то уравнение теплопроводности принимает вид
, то уравнение теплопроводности принимает вид
 , (10)
, (10)
где 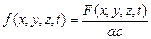 .
.
Уравнения (9) и (10) получены при условии отсутствия теплового обмена между поверхностью тела и внешней средой.
Для тела V граничные условия определяются на его поверхности. Поскольку вдоль поверхности S тело V граничит с окружающей средой, то в каждой точке S необходимо задать либо температуру u, либо тепловой поток 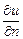 (n – нормаль к S), либо теплообмен (перепад температур) с окружающей средой. Таким образом, граничное условие может быть задано одним из возможных способов:
(n – нормаль к S), либо теплообмен (перепад температур) с окружающей средой. Таким образом, граничное условие может быть задано одним из возможных способов:
1) 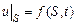 , где
, где  – известная функция точек поверхности S и времени t;
– известная функция точек поверхности S и времени t;
2) 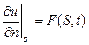 , где
, где 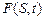 – заданная функция точек поверхности S и времени t;
– заданная функция точек поверхности S и времени t;
3) при теплообмене с окружающей средой граничные условия в общем случае имеют вид

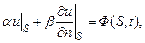 где
где 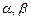 – константы; Ф – заданная функция.
– константы; Ф – заданная функция.
Начальные условия для уравнения теплопроводности запишутся  ,
,
где 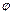 – заданная функция точек тела V.
– заданная функция точек тела V.
30. Уравнение диффузии. Диффузией называется распространение вещества в какой-либо среде, обусловленное неравномерностью в ней его концентрации и происходящее лишь за счет теплового движения молекул.
Уравнение диффузии соли в растворителе.
Уравнение диффузии нейтронов в реакторе.
40. Телеграфные уравнения.
§ 3. Методы решения уравнений математической физики
10. Метод Д’Аламбера. Одним из широко используемых способов решения уравнения колебаний струны является метод характеристик, называемый в этом случае методом Д`Аламбера. Рассмотрим задачу Коши для бесконечной однородной струны: требуется найти решение волнового уравнения
 (1)
(1)
при начальных условиях
 ;
;  (2)
(2)
(рассматриваются только свободные колебания струны).
Формула Д ’ Аламбера для решения задачи Коши для бесконечной струны:
 . (3)
. (3)
20. Метод Фурье решения волнового уравнения. Рассмотрим задачу колебаний конечной струны, закрепленной в точках  и
и  , состоящую в решении волнового уравнения (1),
, состоящую в решении волнового уравнения (1),  ,
, 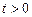 при начальных условиях
при начальных условиях
 (4)
(4)
и при краевых условиях
 . (5)
. (5)
Метод Фурье (разделения переменных) заключается в отыскании решения в виде 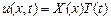 .
.
Можно показать, что решением уравнения (1) будет функция
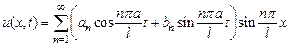 . (6)
. (6)
где, учитывая начальные условия (4),
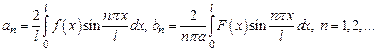 (7)
(7)
30. Решение задачи Коши для уравнения теплопроводности методом пребразования Фурье. Рассмотрим задачу Коши о распространении теплоты в неограниченном стержне, боковая поверхность которого теплоизолирована. В математической постановке она сводится к отысканию решения 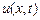 однородного уравнения теплопроводности
однородного уравнения теплопроводности
 (8)
(8)
удовлетворяющего начальному условию
 . (9)
. (9)
Решение, задачи Коши о теплопроводности бесконечного стержня, имеет вид
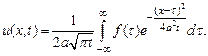 (10)
(10)
Пример 7. Найти решение уравнения 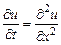 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 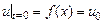 и краевому условию
и краевому условию  .
.
Решение. Имеем дифференциальное уравнение теплопроводности для полубесконечного стержня. Решение, удовлетворяющее указанным условиям, имеет вид 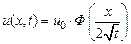 . □
. □
В случае стержня, ограниченного с обоих концов  и
и  , смешанная задача состоит в том, чтобы найти решение уравнения
, смешанная задача состоит в том, чтобы найти решение уравнения  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 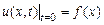 и двум краевым условиям
и двум краевым условиям
1) 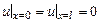 . В этом случае частное решение ищется в виде ряда
. В этом случае частное решение ищется в виде ряда
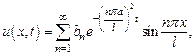 где
где  ;
;
2) 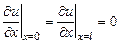 . В этом случае частное решение ищется в виде ряда
. В этом случае частное решение ищется в виде ряда
 где
где  .
.
40. Решение задачи Дирихле для уравнения Лапласа в круге методом Фурье. Уравнение теплопроводности для стационарного случая обращается в уравнение Лапласа  . Здесь u есть функция только точки и не зависит от времени. Для задач, относящихся к плоским фигурам, уравнение Лапласа записывается в виде
. Здесь u есть функция только точки и не зависит от времени. Для задач, относящихся к плоским фигурам, уравнение Лапласа записывается в виде
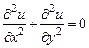 . (11)
. (11)
Задача Дирихле для уравнения Лапласа в круге формулируется следующим образом: найти функцию  , удовлетворяющую уравнению (11) внутри круга радиусом a и граничному условию
, удовлетворяющую уравнению (11) внутри круга радиусом a и граничному условию  на границе этого круга, где f – заданная гладкая функция.
на границе этого круга, где f – заданная гладкая функция.
Введем полярную систему координат  по формулам
по формулам  ,
, 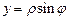 ,
,  ,
, 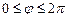 с началом в центре круга. Тогда
с началом в центре круга. Тогда 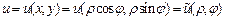 . Решением задачи Дирихле в круге будет функция
. Решением задачи Дирихле в круге будет функция  (13)
(13)
Из краевого условия 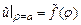 получаем условия для определения коэффициентов
получаем условия для определения коэффициентов
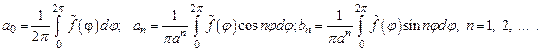 (14)
(14)
Задача. Найти решение уравнения Лапласа в области, заключенной между двумя концентрическими окружностями радиусов 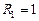 и
и  с центрами в начале координат, удовлетворяющее граничным условиям
с центрами в начале координат, удовлетворяющее граничным условиям  .
.
Граничные условия в полярных координатах примут вид 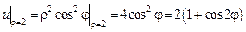 .
.
Решение задачи ищем в виде 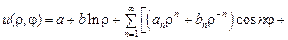
 . Удовлетворим граничным условиям:
. Удовлетворим граничным условиям: ,
, 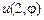
 . Отсюда
. Отсюда 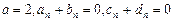 для
для 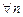 ;
; 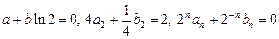 для
для  ,
, 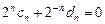 для
для 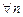 .
.
Из этих двух серий соотношений (линейной алгебраической системы уравнений) определяем коэффициенты: а) 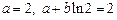
 , б)
, б) 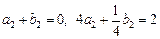
 ,
,
в) все остальные коэффициенты равны нулю. Итак,  , или в декартовых координатах
, или в декартовых координатах  ,
, 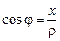 ,
, 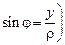
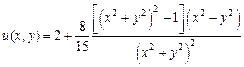 .
.
|
Дата добавления: 2013-12-13; Просмотров: 3587; Нарушение авторских прав?; Мы поможем в написании вашей работы!