Позиционные системы счисления

Управление товарным ассортиментом.

Под товарным ассортиментом принято называть подбор товаров различных видов и разновидностей

Широта товарного ассортиментаопределяется числом входящих в него ассортиментных групп.  

Глубина товарного ассортимента определяется количеством позиций, то есть видов и разновидностей.  

Сопоставимость ассортимента определяется сходством отдельных подгрупп и видов с точки зрения общности конечного использования, каналов распределения, групп потребителей, диапазона цен и прочих характеристик.

Главной задачей при реализации товарной политики является формирование рациональной структуры товарного ассортимента, то есть такой, которая бы с одной стороны способствовала более полному удовлетворению потребностей покупателей, а с другой - обеспечивала бы максимизацию прибыли предприятия.  

Список дополнительной литературы. 1. Закон о РФ «О товарных знаках обслуживания и наименования источника происхождения товара». 2. Патентный закон РФ. 3. Закон РФ "О защите прав потребителей". 4. Котлер Ф. Основы маркетинга: Пер. с анг.- М.: Прогресс, 1990.- гл.8,9. 5. Как добиться успеха: практические советы деловым людям./Под ред. Хруцкого В.Е. - М.: Политиздат, 1991. 6. Пилдич Дж. Путь к покупателю: о том, как преуспевающие компании выпускают товары, которые мы с удовольствием покупаем: Пер. с анг. - М.: Прогресс, 1991. 7. Эванс Дж., Берман Б. Маркетинг: Пер. с анг.- М.: Экономика, 1990.-гл.2,3.

Позиционные и непозиционные системы счисления. Позиционное представление числа. Теорема о представимости числа в натуральной системе счисления. Общий подход к переводу числа из одной натуральной системы счисления в другую.

Системой счисления (СС) называется совокупность правил наименования и записи чисел. Системы счисления подразделяются на позиционные и непозиционные.

В непозиционных системах счисления, возникших значительно раньше позиционных, символы (цифры) не меняют своего значения в зависимости от места (позиции), занимаемой ими в записи числа. Примером такой системы счисления является унарная система, или счетные палочки. Каждая палочка имеет одно и то же значение, равное единице, вне зависимости от места расположения. Другим примером непозиционной системы счисления является римская система. Представление числа в ней короче, чем в унарной, за счет большего числа используемых символов: (I, V, X, L, C, D, M). Например, число 267 записывается в виде CCLXVII. Существующие правила (вычитание младших символов стоящих слева IX, и прибавление стоящих справа XV) не меняют сути дела. Выполнение арифметических действий в таких системах счисления является сложным, а представление дробей не определено.

Система счисления называется позиционной, если значение цифры зависит от ее места в записи числа. Позиционные системы счисления удачно совмещают как простоту представления произвольных чисел, в том числе дробей, так и удобство выполнения арифметических действий. Несмотря на кажущуюся простоту, десятичная позиционная система счисления явилась продуктом длительного исторического развития. Не сразу лучшие умы человечества пришли к тому, чтобы выражать число знаками, придавая им значение не только по форме, но и по месту в записи.

Позиционные СС. Наиболее совершенной из позиционных систем счисления является десятичная. Значение цифры в записи десятичного числа зависит от ее позиции относительно запятой. Так, в числе x = 231,02 цифра 2 в начале записи означает две сотни, а в конце – две сотых доли единицы.

В вычислительной математике вместо слова "позиция" обычно используется слово "разряд". Нумерация разрядов возрастает налево и убывает направо от запятой; первая цифра слева от запятой занимает нулевой разряд. Если мы представим число x в виде ряда по степеням числа 10

x = 231,02 = 2 ∙ 10² + 3 ∙ 10¹ + 1 ∙ 10⁰ + 0 ∙ 10^-1 + 2 ∙ 10^-2,

то увидим, что номер разряда каждой цифры совпадает с показателем степени числа 10 при ней. Число 10 является основанием десятичной системы счисления.

Создание цифровых вычислительных машин не связано с возникновением каких-либо новых принципов представления числа. Запись числа в ЭВМ основана на той же идее, что и в десятичной системе счисления. Сформулируем общие положения позиционного представления числа.

Любая позиционная система счисления характеризуется своим основанием и базисными числами. Основание > 1 – целое положительное (натуральное) число. Базисные числа тоже целые, их количество равно .

Если базисные числа образуют совокупность 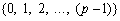, то система счисления называется натуральной.

Любое неотрицательное число может быть представлено в виде ряда

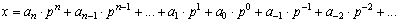
(8.1)

Запись числа 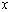в -ичной СС сводится к перечислению коэффициентов ряда (8.1) с указанием знака числа и положения запятой

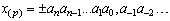
(8.2)

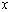Запись (8.2) называется -ичной дробью числа . Дробь может быть как конечной, так и бесконечной.

Приведем примеры наиболее распространенных натуральных систем счисления.

1. Двоичная СС: = 2, базисные числа .

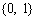2. Десятичная СС: = 10, базисные числа .

3. Шестнадцатеричная СС: = 16, базисные числа .

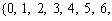
Рассмотрим теорему.

Теорема. Если базисные числа образуют совокупность

то любое вещественное число x может быть представлено в виде p -ичной дроби.

Доказательство. Покажем, что любое число 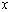может быть представлено в виде ряда (8.1), где a_i принимают свои значения из совокупности 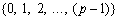. Очевидно, что достаточно рассмотреть лишь положительные числа .

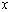Существует целое число такое, что выполняются соотношения

(8.3)

Из совокупности выбираем наибольшее число 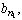для которого

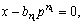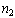Если то ряд (8.1) получен. Если то ищем целое число такое, что

Затем из совокупности B выбираем число для которого

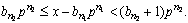
В силу (8.3) заключаем, что Если то получение ряда (8.1) закончено, иначе снова рассматриваем случай

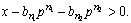
Продолжая этот процесс, получаем последовательность чисел 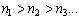и чисел 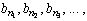выбираемых из совокупности B. При этом либо при некотором k

(8.4)

либо для всех k

(8.5)

В силу полноты пространства вещественных чисел (8.4) и (8.5) означают, что

В данном случае представление числа x в p -ичной системе счисления имеет вид бесконечной дроби. Числа 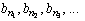образуют последовательность ненулевых коэффициентов искомой p -ичной дроби. Теорема доказана.

Поясним ход доказательства теоремы на примере представления десятичного числа x = 137₍₁₀₎ в натуральной системе счисления с базисными числами . Ясно, что речь идёт о 5-ричной СС.

Из соотношения находим n ₁ = 3. Выбираем b _n1 : 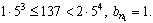Поскольку 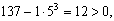то поиск продолжаем. Из получаем n ₂ = 1; так как

Вычисляем разность Следовательно, процесс требует продолжения. Дальнейший подбор даёт n ₃ = 0 и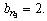

Запишем ряд (8.1) для числа x:

Следовательно, x = 1022₍₅₎

Представление числа в различных натуральных системах счисления. Пусть известна запись числа 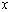в -ичной системе счисления

.

Требуется найти его запись в 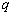- ичной системе счисления

.

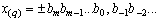Общий подход. В общем случае алгоритм перевода чисел из системы счисления с основанием p в систему счисления с основанием q основан на определении позиционной системы счисления, в которой любое неотрицательное вещественное число x представимо в виде ряда (8.1):

Для нахождения q -ичной записи числа x коэффициенты a_i полинома (8.1) и основание p надо перевести в q -ичную систему счисления, подставить их в (8.1) и вычислить полученный ряд по правилам q -ичной арифметики.

Заметим, что применение общего подхода требует знания q -ичных эквивалентов p -ичных базисных чисел (это не трудно при q > p), а также умения выполнять арифметические действия в q -ичной системе счисления. Последнее зачастую проблематично, поэтому общий подход применяется на практике только для q = 10, так как 10-ичная арифметика нам хорошо известна, и называется алгоритмом замещения. Он будет рассмотрен ниже. Для других случаев разработаны свои эффективные алгоритмы, позволяющие осуществить перевод с минимумом вычислений, выполняемых также в рамках 10-ичной арифметики.

Дата добавления: 2013-12-13