Дифференциал функции и его применение в приближенных вычислениях

Графики производных функций

В практической медицине часто приходится сопоставлять график изменения некоторой величины, например, со временем с графиком производной этой величины. В частности, в методе, называемом реопародонтография регистрируется зависимость объема кровенаполнения V исследуемого участка сосудистой системы от времени, т.е. V(t), и зависимость первой производной этой функции, которая определяет изменение скорости кровенаполнения. Примеры можно продолжить.

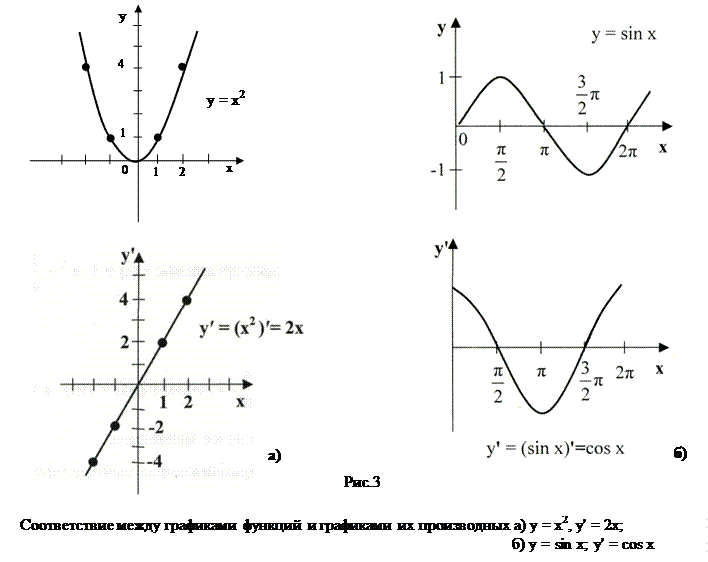Для нескольких простых функций приведем графики самих функций и их производных.

Дифференциал заданной функции y = f(x) равен произведению значения производной этой функции в данной точке x ₀ на дифференциал аргумента (d – символ дифференциала):

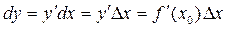(7)

Дифференциал независимой переменной равен приращению этой переменной: dx = Δx.

Дифференциал функции равен ее приращению только при достаточно малых приращениях Δх:

Δy ≈ dy (8)

Из формулы (7) с учетом соотношения (8) получаем:

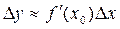, (9)

Формула (9) может использоваться для нахождения приближенного приращения функции и оценки значения градиента функции в соответствии с соотношением (6).

Приведем несколько примеров.

1. Найдем приближенное приращение функции y = 2x² + 7 при x ₀ = 2 и

Δx = 0,0001.

Решение: 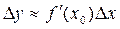; y' = 4x или Δy ≈ 4x Δx

Таким образом, Δу ≈ 4 · 2 · 0,0001 = 0,0008.

2. Рассмотрим шарообразную клетку радиуса R (например, эритроцит в венозном русле), которая увеличивается в объеме, не изменяя формы. Объем 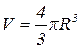(V = f(R)). Оценим изменение объема клетки ΔV, если ее радиус увеличился от 2,5 · 10^-3 до 2,6· 10^{-3 см}.

Решение: ΔV≈ dV = V'dR = 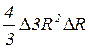= 4π R²ΔR = 7,85 · 10^-9 см³.

Дата добавления: 2013-12-13