Вычисление радиуса сходимости

Признак Вейерштрасса (равномерной сходимости функционального ряда).

Функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

Другими словами, если функции в некоторой области 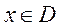не превосходят по абсолютной величине соответствующих положительных чисел и если числовой ряд сходится, то функциональный ряд 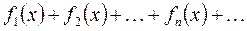в этой области сходится равномерно.

Пример. Доказать равномерную сходимость функционального ряда .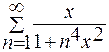

Решение. . Заменим общий член этого ряда общим членом числового ряда, но превосходящего каждый член ряда по абсолютной величине. Для этого надо определить 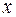, при котором общий член ряда будет максимальным.

.

.

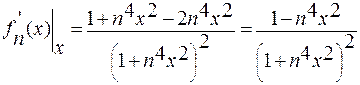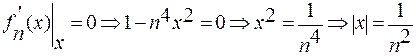Тогда .

Полученный числовой ряд сходится, значит, функциональный ряд сходится равномерно согласно признаку Вейерштрасса.

Пример. Найдите сумму ряда .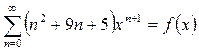

Для нахождения суммы ряда воспользуемся известной формулой для суммы геометрической прогрессии

Дифференцируя левую и правую части формулы (1), получим последовательно

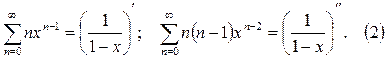
Выделим в сумме, подлежащей вычислению, слагаемые, пропорциональные первой и второй производной:

.

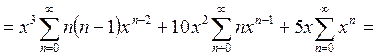
Вычислим производные:

тогда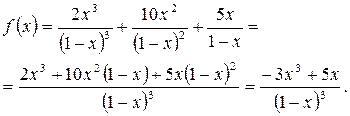

Степенные ряды.

Среди функциональных рядов есть класс степенных и тригонометрических рядов.

Определение. Функциональный ряд вида

называется степенным по степеням 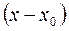. Выражения 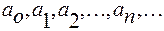- постоянные числа.

Если ряд 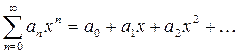является степенным по степеням .

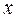Область сходимости степенного ряда. Теорема Абеля.

Теорема. Если степенной ряд 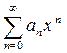сходится в точке 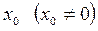, то он сходится и притом абсолютно для всякого значения 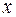, по абсолютной величине меньшего 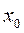, то есть или в интервале .

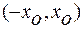Доказательство.

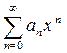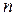Вследствие сходимости рада его общий член должен стремиться к нулю, поэтому все члены этого ряда равномерно ограничены: существует такое постоянное положительное число , что при всяком имеет место неравенство .

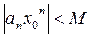Тогда данный ряд можно записать так:

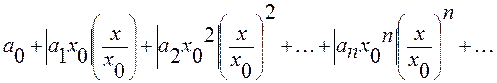
В силу сделанного замечания можно записать ряд

, который образует геометрическую прогрессию со знаменателем 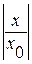. Если , то , и прогрессия сходится. Если больший ряд сходится, то будет сходиться и данный ряд. Теорема доказана.

Следствие. Если степенной ряд расходится при значении , то ряд расходится при всяком значении 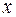, большем по абсолютной величине , .

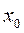Из теоремы Абеля и следствия из этой теоремы вытекает следующее предположение. Для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число , что для всех 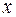, , ряд абсолютно сходится, а для значений 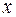, , 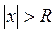ряд расходится.

Что касается значени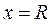й или 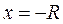, то здесь возможны ситуации, когда ряд сходится в обеих точках, или только в одной из них, или ни в одной.

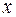Определение. Число такое, что для всех , , степенной ряд сходится, а для всех , , 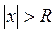расходится, называется радиусом сходимости ряда, а интервал 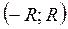называется интервалом сходимости.

Для ряда 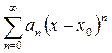интервал сходимости имеет вид с центром в точке

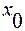
Для ряда 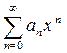интервал сходимости имеет вид 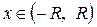с центром в точке

-R cx. R x

расх ₀ расх

В граничных точках поведение ряда требует дополнительного исследования.

Можно указать правило для нахождения радиуса сходимости степенного ряда.

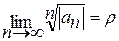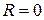Теорема. Если существует предел , то радиус сходимости ряда равен , то есть , причем считаем , если , и , если .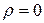

Доказательство.

Предположим, что 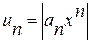, то есть рассмотрим числовой ряд , который является рядом абсолютных величин данного степенного ряда.

Тогда :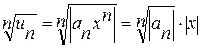

1. Пусть 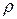- конечное число, отличное от нуля, значит, 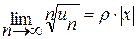. По радикальному признаку Коши ряд, составленный из абсолютных величин ряда, сходится при 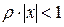, отсюда следует, что 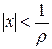. При и 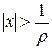ряд расходится для всех значений .

В самом деле, если бы при , , ряд сходился, то по теореме Абеля для 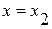, где 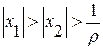, он должен был бы сходиться, чего быть не может. Таким образом, ряд сходится при 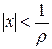и расходится при 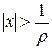и, значит, .

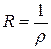2. Пусть 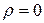. Тогда 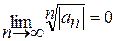при всяком значении , и ряд сходится для любого . Значит, ряд абсолютно сходится во всякой точке ос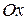и и .

3. Пусть . Тогда 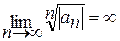при всяком значении , , 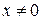и значит, ряд не может сходиться ни при каком 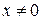. На основании теоремы Абеля заключаем, что ряд во всех точках оси 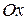(кроме нулевой) расходится и .

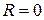Теорема. Если , то радиус сходимости ряда равен 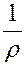, то есть , причем мы считаем при и при .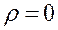

Степенные ряды в области сходимости сходятся абсолютно и поэтому можно использовать признаки сходимости рядов с положительными членами.

1. По признаку Даламбера:

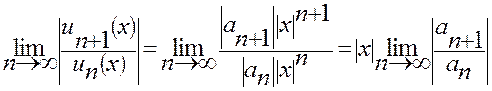
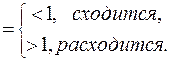
Ряд сходится, если , отсюда радиус сходимости - .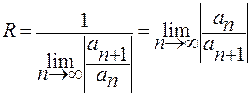

2. По интегральному признаку Коши:

Ряд сходится, если 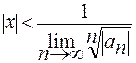, отсюда следует, что .

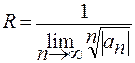Пример. Найдите область сходимости рядов: 1) и 2) .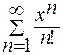

1) .

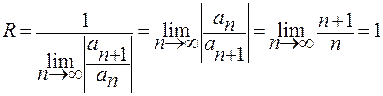Интервал сходимости

Исследуем граничные точки.

расходится;

- сходится условно по признаку

Лейбница.

Область сходимости ряда .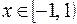

2) 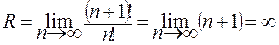, ряд сходится при всех .

Дата добавления: 2013-12-13