Дифракционная решетка

Дифракционная решетка представляет собой стеклянную или металлическую пластинку, на которой нанесено очень много (иногда до сотен тысяч) прямых равноотстоящих штрихов одинаковой конфигурации. Таким образом образуется совокупность прозрачных и непрозрачных участков.

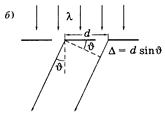
Рассмотрим простейшую идеализированную решетку, состоящую из одинаковых равноотстоящих щелей в непрозрачном экране. Пусть ширина каждой щели равна b, а непрозрачного участка а, период решетки — d=b+a. В решетке реализуется многолучевая интерференция когерентных дифрагированных пучков света, исходящих из каждой щели решетки при ее освещении.

Дифракционную (точнее дифракционно-интерференционную) картину наблюдают по методу Фраунгофера, т.е. в параллельных лучах, а практически Рис.3.9.4.

— в фокальной плоскости объектива (рис.3.9.4 a).

Пусть плоская монохроматическая световая волна падает на решетку нормально. Каждая из щелей в отдельности давала бы в фокальной плоскости объектива дифракционную картину, показанную на рис.3.9.3. И такие картины от всех щелей в отсутствие когерентности точно накладывались бы друг на друга, независимо от их положения. Интенсивности при этом складывались бы, и мы получили бы при наличии N щелей дифракционную картину как от одной щели, но усиленную в N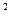 раз.

При освещении же решетки когерентным светом, световые волны от всех щелей интерферируют друг с другом, и дифракционная картина резко меняется. Мы будем наблюдать систему достаточно узких максимумов.

Главные максимумы. В середину дифракционно-интерференционной картины когерентные колебания от всех щелей приходят в фазе. Это значит, что если амплитуда от одной щели равна A ₁, а число щелей в решетке N, то результирующая амплитуда A и соответствующая ей интенсивность I будут определяться формулами

Такой же результат получается и при углах дифракции , для которых оптическая разность хода D колебаний от соседних щелей (рис.3.9.4 б) равна целому числу длин волн:

m = 1, 2, … (3.9.4)

где знаки «±» следуют из симметрии дифракционной картины относительно нормали к решетке (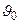= 0): при знаке плюс угол > 0, а при знаке минус - угол < 0.

В направлениях , определяемых этим уравнением, возникают максимумы, интенсивность которых в N ² раз превосходят интенсивность от каждой щели в том же направлении. Их называют главными максимумами m -го порядка, а уравнение (3.9.4) — условием главных максимумов. Именно главные максимумы и представляют особый практический интерес. Как мы увидим далее, они получаются тем более узкими и резкими, чем большее число N штрихов содержит решетка.

Интерференционные минимумы. Для выяснения дальнейших деталей фраунгоферовой дифракционной картины воспользуемся векторной диаграммой, которая позволит легко найти и результирующую амплитуду A колебаний, приходящих в произвольную точку P фокальной плоскости объектива (рис.3.9.5).

Векторная диаграмма в нашем случае пред-

ставляет собой цепочку векторов-амплитуд Рис.3.9.5.

когерентных колебаний, приходящих в точку P

от каждой из N щелей: A ₁, A ₂,..., A_N (рис.3.9.5 a). По модулю эти векторы одинаковы, и каждый следующий отстает от предыдущего (или опережает, это не существенно) по фазе на один и тот же угол g. Этот угол связан с оптической разностью хода D соответствующих лучей от соседних щелей при нормальном падении света на решетку соотношением:

(3.9.5)

где d — период решетки.

Теперь проследим, как будет вести себя эта цепочка векторов (а значит и ее замыкающая A) при удалении точки P от фокуса F, т. е. с ростом угла дифракции .

Ясно, что при этом будет увеличиваться разность фаз g между колебаниями от соседних щелей, и цепочка векторов будет постепенно закручиваться. Первый раз она замкнется и вектор A обратится в нуль, когда угол Ng станет равным 2 π — это непосредственно видно из рис.3.9.5 б.

При дальнейшем росте угла , а значит, разности фаз g и Ng, цепочка будет периодически то распрямляться (главные максимумы, А = макс), то замыкаться (интерференционные минимумы, А = 0). Последнее будет происходить при значениях угла Ng кратных 2 π:

(3.9.6)

где m’ принимает целочисленные значения, кроме 0, N, 2 N,..., при которых цепочка распрямляется, и мы получаем главные максимумы.

Подставив в (3.9.6) значение g из формулы (3.9.5), получим:

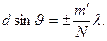(3.9.7)

Это выражение представляет собой условие для интерференционных минимумов (при целочисленных значениях m’, кроме 0, N, 2 N,...). Оно же содержит и условие (3.9.4) для главных максимумов (при m’ = 0, N, 2 N,...). Между двумя соседними главными максимумами расположены N – 1 интерференционных минимумов. А между последними, в свою очередь, — добавочные максимумы, интенсивность которых при достаточно большом числе N штрихов решетки пренебрежимо мала (она составляет не более 5% от интенсивности главных максимумов).

В отличие от условия (3.9.4), которое дает только положения главных максимумов, соотношение (3.9.7) позволяет определить и их угловую ширину. В самом деле, при переходе от главного максимума к соседнему минимуму (рис.3.9.6) m’ меняется на единицу, например от N до N + 1. Тогда при достаточно большом N угловую полуширину 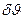главного максимума 1-го порядка Рис.3.9.6.

можно найти, взяв дифференциал уравнения (3.9.7)

с учетом того, что m’ при этом меняется на единицу (dm’ = 1). Тогда , откуда

(3.9.8)

Обращает на себя внимание тот факт, что 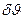зависит не от d и N в отдельности, а от их произведения, которое есть не что иное, как ширина решетки h = Nd. С ростом угла дифракции ширина главных максимумов увеличивается. Главные максимумы будут тем уже, чем больше ширина решетки h и меньше угол дифракции .

Теперь выясним, что означает утверждение, например, «угловая ширина главного максимума 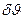мала». По сравнению с чем? Ответ достаточно очевидный: величину 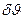надо сравнивать с угловой шиной D d между соседними главными максимумами. Если 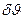«D d, мы говорим, что главные максимумы узкие (резкие). Оценим отношение этих двух величин. Значение 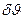соответствует изменению m’ в (3.9.7) на единицу, но таких значений m’ между двумя соседними главными максимумами оказывается N. Считая, что на каждый интервал dm’ = 1 приходится одно и то же значение 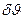(для оценки), приходим к выводу, что 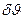в N раз меньше, чем D d. Итак, резкость главных максимумов пропорциональна числу штрихов решетки (более точный расчет приводит к тому же результату).

Таким образом, с помощью условий (3.9.4) и (3.9.7) мы можем установить не только положения главных максимумов, но и их угловую ширину (резкость). Остается решить вопрос об их интенсивности. Рассмотрим его сначала качественно.

Прослеживая поведение векторной диаграммы по мере увеличения угла дифракции , мы оставили без внимания тот факт, что при этом каждый вектор цепочки по модулю будет уменьшаться, ибо он определяется дифракцией от каждой щели. Результирующий вектор при закручивании цепочки будет сначала уменьшаться и в дальнейшем вести себя аналогично тому, как показано на рис3.9.3 зависимости I от sin.

Следовательно, кроме интерференционных минимумов, необходимо иметь в виду и д ифракционные минимумы, определяемые условием (3.9.1), т. е.

где b — ширина каждой щели.

При этом условии все векторы цепочки обращаются в нуль, значит и результирующая интенсивность в этих направлениях всегда должна быть равна нулю. Даже в том случае, если этому направлению соответствует главный максимум m -го порядка.

Интенсивность главных максимумов. Распределение интенсивности в дифракционно-интерференционной картине проще всего получить с помощью векторных диаграмм (рис.3.9.5 и 3.9.2). В итоге получим следующее выражение:

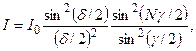(3.9.9)

где, напомним,

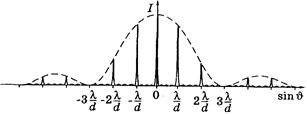
Полученный результат (3.9.9) графически представлен на рис.3.9.7 как зависимость интенсивности дифракционной картины от синуса угла дифракции . Как видим, интерференция многих пучков привела Рис.3.9.7.

к резкому перераспределению интенсивности света, обусловленному дифракцией от каждой щели.

Первая дробь в выражении (3.9.9) представляет собой плавную функцию от sin(она показана пунктиром на рисунке и отражает дифракционное распределение интенсивности от каждой щели). Эта плавная функция модулирует многолучевую интерференционную картину от N щелей, которую описывает вторая дробь в формуле (3.9.9).

Практически наиболее важными являются главные максимумы, попадающие в центральный дифракционный максимум от каждой щели — они являются наиболее интенсивными.

Дата добавления: 2013-12-13