Доведення

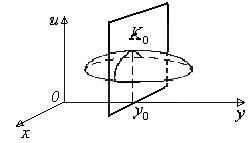
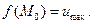Крива - лінія перетину поверхні 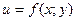й площини 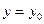, тоді задана рівнянням Аналогічно доводиться, що 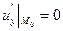й ін. випадки.

Приклад.

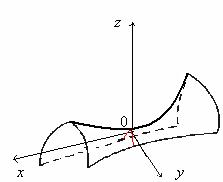
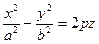, (р>0) –

гіперболічний параболоїд.

,

.

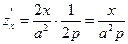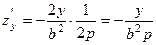У точці 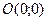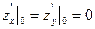, однак у точці 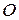екстремуму немає, тому що в 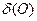порушуються визначення максимуму, мінімуму.

Лекція 28

96. Достатня ознака існування екстремуму

Теорема. Нехай у 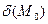функція 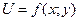має неперервні частинні похідні до 3-го порядку включно і точка 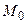є стаціонарною, тоді:

1) при 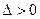є екстремум, якщо , то в точці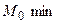, якщо ,то в точці ;

2) при 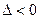- екстремуму немає;

3) при 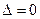- потрібні додаткові дослідження.

Тут

Доведення. За формулою Тейлора

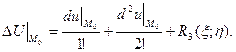Оскільки точка 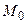- стаціонарна, то .

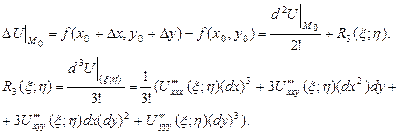
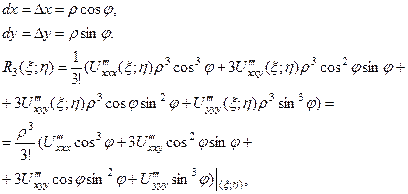оскільки похідні неперервні, то вони обмежені; 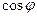, 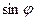- обмежені, то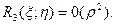

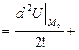
Таким чином 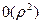, отже:

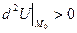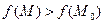1) якщо , то і в точці ;

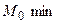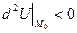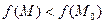2) якщо , то і в точці ;

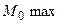3) якщо , то необхідні додаткові дослідження;

4) якщо 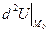змінює знак, то екстремуму немає, тому що порушується визначення максимуму, мінімуму.

Використовуючи означення других похідних, обчислених в точці 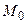, одержимо:

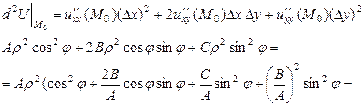
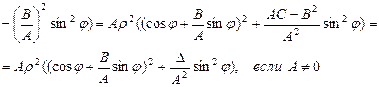
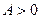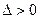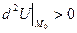
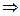1) якщо ,, то точка ;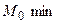

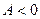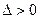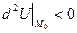
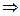якщо ,, то точка ;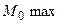

2) якщ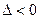о , то

при ,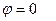

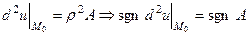при , що є розв’язком рівняння ,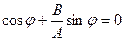

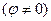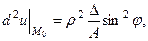
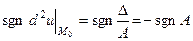. Таким чином, 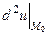змінює знак, отже, при 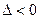екстремуму немає;

3) якщо 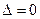- потрібні додаткові дослідження.

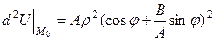і 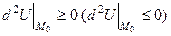залежно від знака А і значення кута .

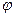Приклад.

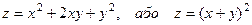
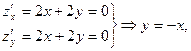всі точки прямої 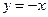підозрілі на екстремум.

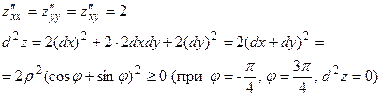
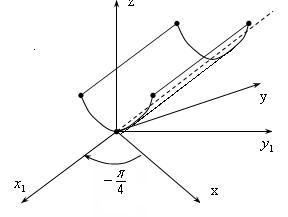
У цьому випадку екстремум будемо називати нестрогим, тобто в точках, що лежать на прямій 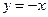, нестрогий мінімум.

Зауваження. Якщо осі x, y розгорнути на кут 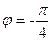, то, використовуючи формули переходу 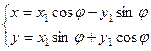, отримаємо

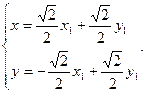Тут 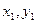- нові координати.

Рівняння 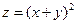в новій системі координат: 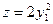, таким чином, ми розглядаємо параболічний циліндр.

97. Умовний екстремум

Визначити екстремум функції 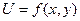, якщо змінні x і y зв'язані умовою

Тут функція U двічі диференційована по x, y і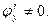

Оскільки з умови 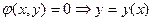, то 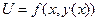- функція однієї змінної, з огляду на це визначимо точки, підозрілі на екстремум:

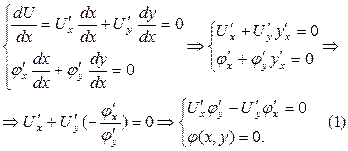
Система (1) дозволяє визначити точки, підозрілі на екcтремум, тому що використовували тільки необхідну умову існування екстремуму. Для достатньої умови існування екстремуму у точці 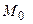визначимо

і за знаком 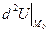(див. пункт 96) установлюємо наявність екстремуму і його вигляд.

Приклад. У точках 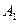і 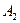перебувають джерела світла інтенсивності 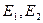відповідно. Визначити точку, у якій висвітлення буде мінімальним. Нехай .

.

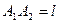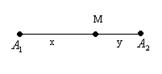
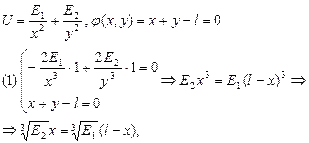
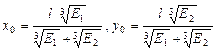Точка 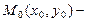підозріла на екстремум.

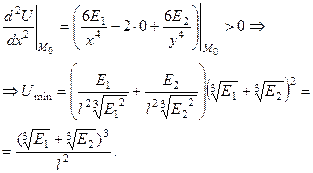
Таким чином, =.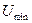

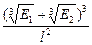Лекція 29

98. Найбільше й найменше значення функції в замкненій області

Схема визначення 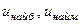в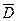

1. Для функції 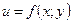визначаємо точки, підозрілі на екстремум із системи .

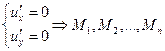2. Визначаємо значення функції 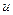в тих точках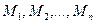, які належать області .

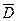3. Оскільки функція 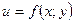на границі 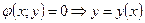є функцією однієї змінної: 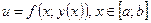, то найбільше й найменше значення цієї функції знаходяться на кінцях відрізка 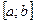або у внутрішніх точках, підозрілих на екстремум. Визначаємо значення функції в цих точках і на кінцях відрізка (для дослідження на границі можна використовувати пункт 97).

4. Із всіх отриманих значень функції 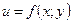вибираємо найбільше й найменше.

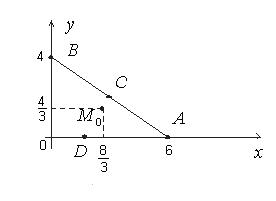
Приклад

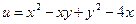; Область 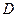обмежена лініями .

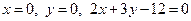1. .

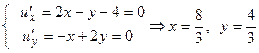Точка 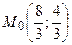підозріла на екстремум і.

.

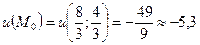1) Границя області 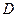розпадається на три частини.

~.

,

, ,

.

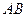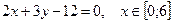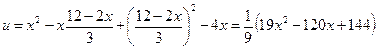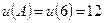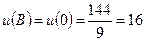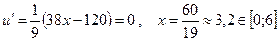Точка 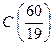, що лежить на границі 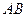, підозріла на екстремум.

,

~ ,

, .

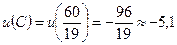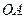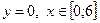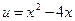Точка , що лежить на границі 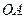, підозріла на екстремум.

,

,,

~ ,

.

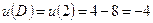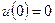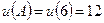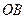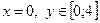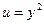
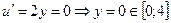Цю точку ми вже досліджували, вивчаючи границю .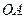

2) Вибираємо найменше й найбільше значення:

.

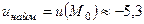
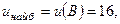99. Задача про об'єм криволінійного циліндра

.

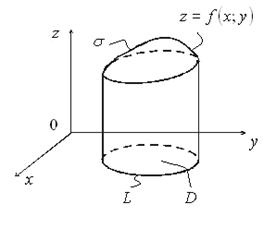
Криволінійний циліндр – це тіло, що обмежене циліндричною поверхнею (напрямна – крива , твірні паралельні осі 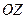), площиною 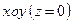й поверхнею .

.

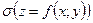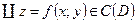Для визначення об'єму криволінійного циліндра розіб`ємо область 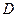довільним чином на 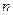частин.

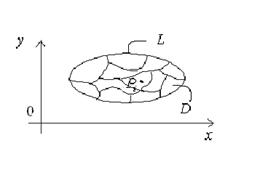
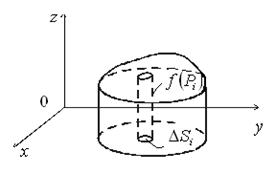
На кожній ділянці довільним чином вибираємо точки 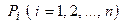й обчислюємо .

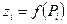Позначимо площу кожної ділянки через . Побудуємо прямі циліндри з нижньою основою 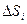й висотою 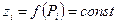. Ясно, що об'єм криволінійного циліндра наближено дорівнює сумі об'ємів таких “волокон” – прямих циліндрів: .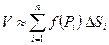

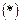Суму 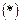називають 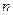-ю інтегральною й вона залежить від способу розбиття області 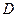й вибору точок 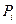, і чим дрібніше розбиття, тим точніша рівність 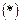. Навколо кожного 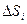опишемо коло з діаметром.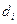 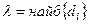називається рангом розбиття. Якщо 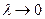, то й усі 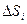стягуються в точки.

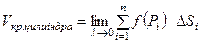
Означення. Якщо границя послідовності 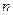–х інтегральних сум 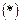при 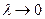існує, то вона називається подвійним інтегралом від функції 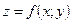по області 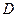й позначається .

Лекція 30

100. Задача про визначення маси неоднорідного тіла

Нехай густина у кожній точці обмеженої області V описується неперервною й додатно визначеною функцією .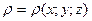

Розіб'ємо область V довільним чином на n частин і в кожній частині довільно виберемо (·) 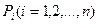. Позначимо об`єм кожної частини через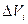 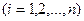. Обчислимо густину 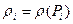. Оскільки , а об’єм 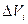дуже малий, то можна вважати, що густина для цієї частини й дорівнює 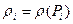, тоді маса цього нескінченно малого елемента 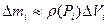, а маса всієї області

(**),

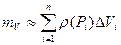n-а інтегральна сума (**) залежить від способу розбиття області V і вибору точок 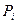, чим дрібніше розбиття, тим точніша рівність (**). Навколо кожної частини 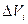опишемо сферу з діаметром 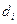. Ранг розбиття 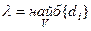, й чим дрібніше розбиття, тим ближче 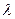до нуля.

.

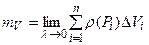Означення. Якщо границя послідовності n-х інтегральних сум (**) при 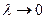існує, то він називається потрійним інтегралом від функції 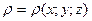по області V і позначається .

Зауваження. Аналогічно можна визначити кратний інтеграл в n-мірному просторі, де точки 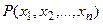має n координат, 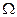- обмежена область n-вимірного простору, функція :

,

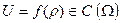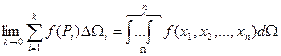
тут 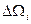- міра нескінченно малого елемента (н.м. елемента) довільного розбиття області 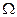, 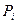- довільна точка цього н.м. елемента, 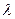- ранг розбиття.

101. Формулювання теореми про існування кратного інтеграла

Якщо 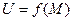Î 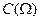, 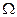- зв'язана, обмежена й замкнена область, то f(M) інтегрована в області 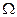, тобто границя n-ї інтегральної суми існує, не залежить від способу розбиття області 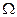й вибору точок .

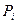Зауваження. У пункті 62 наведено доведення інтегрованості функції однієї змінної, яка є частковим випадком ФДЗ. Аналогічно доводиться й дана теорема, тобто шляхом визначення границь верхньої й нижньої сум Дарбу.

102 Властивості кратних інтегралів

Виходячи із властивостей границь і кінцевих сум, можна записати такі властивості кратних інтегралів:

1) 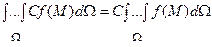, де С – const;

2) ;

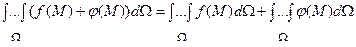3) якщо область 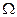розбивається на дві області 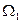й 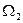без спільних внутрішніх точок, то

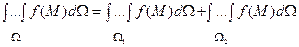
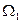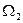(у доведенні останньої властивості беремо загальну границю областей і однієї з поверхонь розбиття);

4) якщ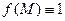о , то 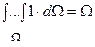- міра області інтегрування;

5) якщо m, M – найменше й найбільше значення підінтегральної функції f(M) в області інтегрування з мірою 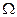, то

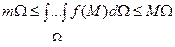
(доведення випливає зі справедливості нерівності:

).

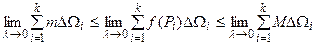103 Теорема про середнє

Якщо 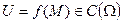, 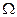- зв'язана, обмежена й замкнена область, то в 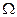знайдеться принаймні одна така точка 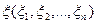, що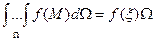

(доведення випливає із властивості 5 і неперервності функції 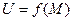, див. п.64).

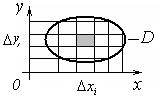
104. Обчислення кратних інтегралів

Означення. Плоска область D називається правильною в напрямку осі OY, якщо будь-яка пряма, паралельна осі OY, перетинає її границю не більш ніж у двох точках.

Теорема. Подвійний інтеграл від неперервної функції по правильній області D дорівнює повторному інтегралу від цієї функції по області D, тобто

.

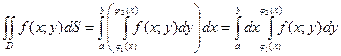Доведення

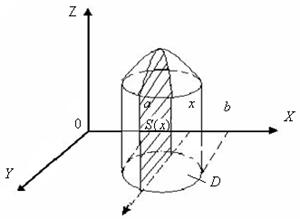
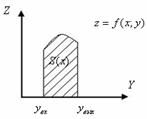З одного боку, 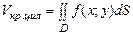, з іншого .

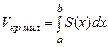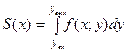як площа криволінійної трапеції.

Остаточно: .

Приклад. Обчислити 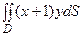, якщо ,

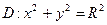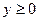
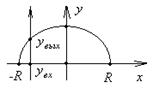
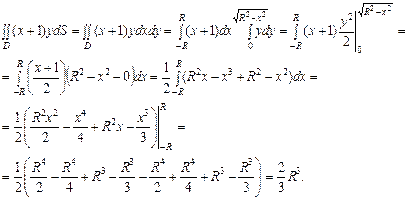
Лекція 31

105. Заміна змінних у кратних інтегралах

З теореми про існування кратних інтегралів (п.101) випливає, що інтеграл не залежить від способу розбиття області D.

1. Декартова система координат

Розбиваємо область D лініями , .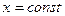

.

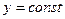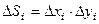
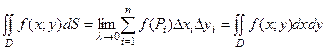Таким чином, у декартовій системі координат .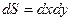

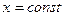
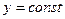
Для потрійного інтеграла 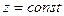- площини, які розбивають область V на нескінченно малі прямокутні паралелепіпеди й .

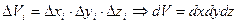1. Полярна система координат

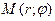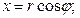
У цій системі координат точка : 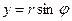формули переходу. У цьому випадку розбиваємо область D лініями 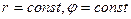, тобто концентричними колами й променями.

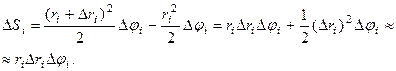
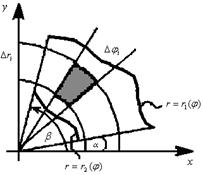
Таким чином, з точністю до нескінченно малих другого порядку малості .

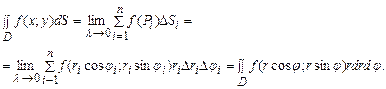
Тобто .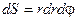

Зауваження. Загальний випадок зміни змінної в подвійному інтегралі дивись п.182.

3. Циліндрична система координат

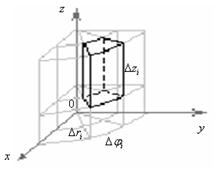
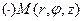, де 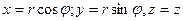- формули переходу. Розбиваємо область V поверхнями 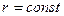, 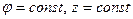концентричні циліндричні поверхні, напівплощини, що виходять із осі OZ, і площини, перпендикулярні до осі OZ.

.

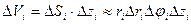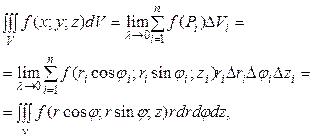
тобто в циліндричній системі координат .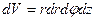

Зауваження. Можна припустити, що при записуванні кратного інтеграла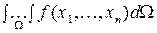 в новій системі координат, де ,

,

……………………

,

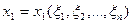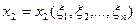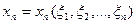диференціал міри 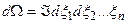, тут множник називають я кобіаном.

Доведено, що якобіан дорівнює:

.

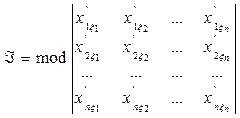Наприклад, у циліндричній системі координат

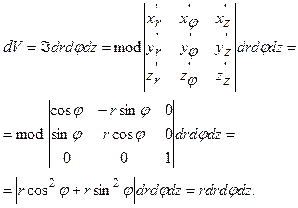
4. Сферична система координат

Оскільки 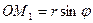, то формули переходу мають вигляд: 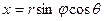, , 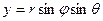, 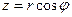при цьому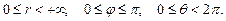

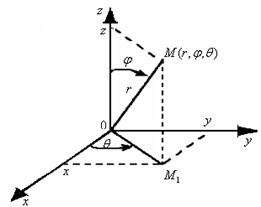
Поверхні розбиття тіла V на нескінченно малі елементи: 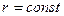- концентричні сфери, - конічні поверхні з вершинами в точці О, 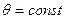- напівплощини, що виходять із осі OZ.

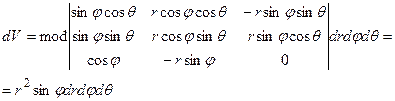
і тоді

.

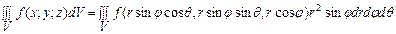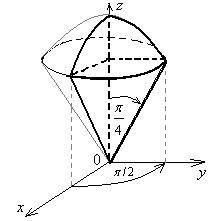
Приклад

Обчислити інтеграл 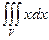, якщо V~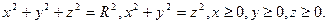

Обчислювати цей інтеграл зручніше у сферичній системі координат

.

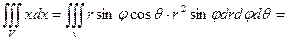
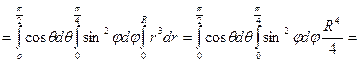
Лекція 32

106. Застосування кратних інтегралів до задач фізики

1. Маса неоднорідної пластини

Надалі під пластиною будемо мати на увазі тіло, що має форму прямого циліндра, для якого h<<S, де h - висота циліндра, S - площа поперечного перерізу, h = const.

Оскільки h мале, то густина не залежить від змінної z, тобто вона не змінюється уздовж будь-якого перпендикуляра до площини x. Розмірність густини .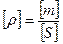

Густина 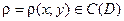, а D – зв'язана, обмежена, замкнена область. Виділяємо елементарну частину області D з площиною dS, яка настільки мала, що можна вважати густину на цій ділянці сталою. Тоді маса елементарної частини 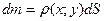, а маса всієї пластини:

.

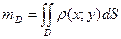Подібні міркування дозволяють уникнути побудови n-ї інтегральної суми й граничного переходу в кожній конкретній задачі.

Зауваження. До таких самих результатів можна прийти, якщо використовувати пункти 100 і 104:

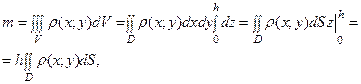
тут розмірність густини .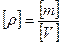

2. Момент інерції

З фізики відомо, що момент інерції матеріальної точки 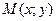щодо осі Ox: 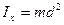, де m – маса, d – відстань від точки до осі. Тоді момент інерції нескінченно малого елемента пластини D визначається за формулою 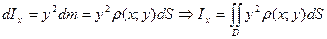. Аналогічно .

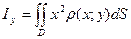Зауваження. Якщо розглядати неоднорідне тіло, то

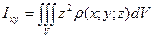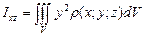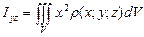, , – моменти інерції щодо відповідних площин, а 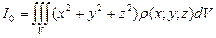– момент інерції щодо полюса О.

3. Центр мас

Позначимо центр мас неоднорідної пластини буквою С, тоді 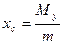, , 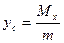де 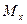, 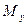– статичні моменти пластини щодо відповідних осей, m – маса пластини.

Статичний момент нескінченно малого елемента пластини:

, , .

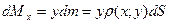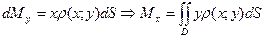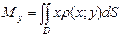Отже, , .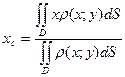

Зауваження. Аналогічно визначаються координати центра мас неоднорідного тіла:

, , .

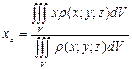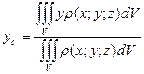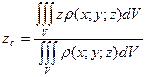107. Вектор-функція скалярного аргументу і її границя

Означення. Якщо 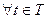відповідає певний вектор 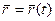, то кажуть, що на множині T визначений вектор-функція скалярного аргументу

.

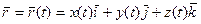Означення. Лінія L, описувана кінцем радіуса-вектора 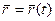, називається годографом вектор-функції.

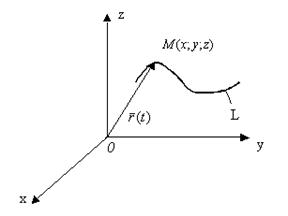
Зауваження. Якщо t – час, то годограф – це траєкторія руху точки .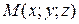

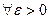
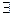
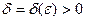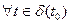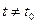
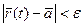Означення. Якщо таке, що при й , то 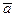називається границею вектор-функції 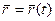при , тобто .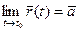

Наслідок. 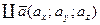, тоді

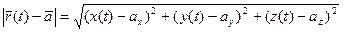. Оскільки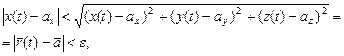

то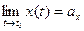, аналогічно , .

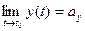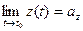Отже, для того, щоб 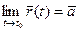, необхідно й достатньо, щоб , , .

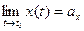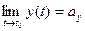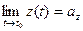Означення. Вектор-функція 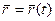називається неперервною в точці 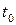, якщо 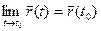, тобт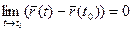о , або .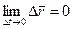

108. Похідна вектор-функції

Означення. Якщо існує границя 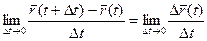, то вона називається похідною вектор-функції й позначається .

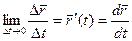Наслідок. Оскільки 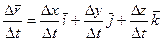, то з існування 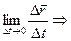існування границь 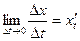, , 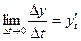і навпаки.

Таким чином для того, щоб 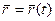мала похідну, необхідно й достатньо, щоб 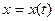, , 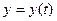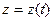були диференційовані.

Лекція 33

109. Геометричний зміст похідної вектор-функції

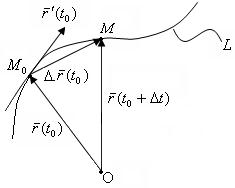
При 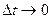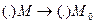й хорда 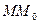розвертається до положення дотичної: .

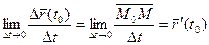Геометричний зміст похідної вектор-функції: 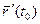лежить на дотичній, проведеній до годографа , і напрямлена у бік зростання параметра .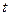

Зауваження. Годограф можна розглядати як графік функції, заданої параметрично:

~.

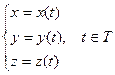Означення. 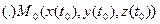називається особливою, якщо 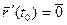або не існує.

Означення. Крива називається гладкою, якщо 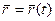неперервно диференційована функція без особливих точок.

Теорема. Довжина нескінченно малої дуги гладкої кривої еквівалентна стягуючій її хорді, тобто

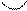
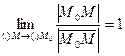(без доведення).

Зауваження. Перша важлива границя є окремим випадком цієї теореми, тому що

.

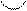
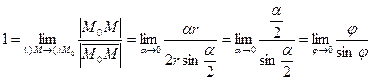110. Дотична й нормальна площини до кривої в просторі

Нехай - гладка крива. Оскільки вектор 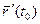лежить на дотичній, то він є напрямним вектором цієї прямої. 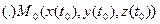- точка дотику.

Рівняння дотичної: .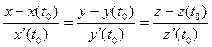

У той же час вектор 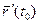перпендикулярний до нормальної площини, тобто

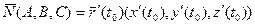
й рівняння нормальної площини:

.

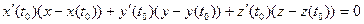111. Механічний зміст похідної вектор-функції

Нехай матеріальна точка рухається по годографу вектор-функції .

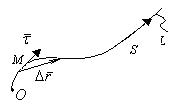
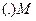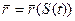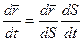Уведемо в розгляд початок відліку точку О і дугову координату S, що спрямована у напрямку руху . Тоді й . Оскільки 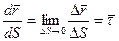, тут 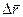- вектор-хорда, 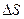- довжина дуги, то за теоремою пункту 109 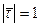, вектор 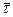лежить на дотичній, тобто 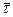- одиничний вектор дотичної, що спрямований у напрямку руху точки 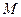, а 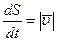. Отже, .

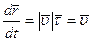Механічним змістом похідної вектор-функції за часом 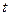є вектор швидкості матеріальної точки 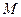під час руху по кривій .

112. Задача про визначення маси неоднорідної матеріальної лінії

Нехай матеріальна лінія є гладкою кривою , що задається вектор-функцією 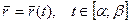. Погонна густина цієї лінії 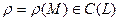. Розмірність густини, де 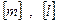- розмірністи маси й довжини лінії.

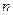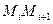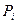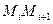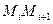
Довільним чином ділимо криву на частин і на кожній дузі вибираємо точку . Вважаємо густину на дузі рівною , тоді маса дуги , де 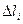- довжина дуги .

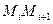Маса всієї матеріальної лінії

(*).

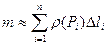І чим дрібніше розбиття, тим точніша ця рівність.

Найбільшу з довжин дуг 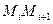позначимо буквою 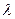й назвемо рангом розбиття. Якщо 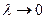, то дуги 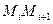стягуються в точки, а 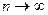. Сума (*) залежить від способу розбиття лінії й вибору точок .

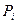Визначимо 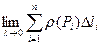, якщо він існує, то його називають криволінійним інтегралом по довжині дуги й позначають .

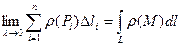Фізичний зміст криволінійного інтеграла по довжині дуги - маса матеріальної лінії

.

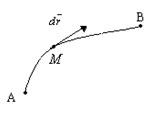
113. Задача про роботу змінної сили під час руху точки по кривій

Нехай точка 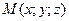рухається уздовж кривої , що є годографом вектор-функції 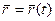. До точки прикладена сила

.

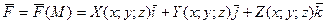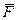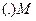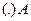Визначити роботу сили при переміщенні з в 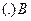, 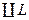- гладка, а 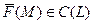. Довільним чином розбиваємо криву 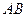на 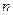частин і на кожній дузі 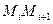вибираємо точку 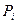. Оскільки дуга 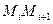досить мала, а 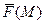неперервна, то можна вважати, що на цій ділянці сила стала й 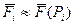. І тоді робота сили 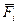на ділянці : .

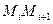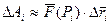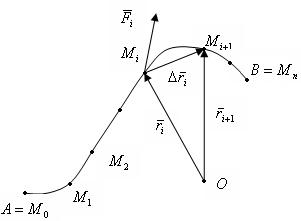
А робота на всій кривій : , і чим дрібніше розбиття, тим точніша ця формула. Найбільшу з довжин дуг позначимо буквою 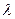, що називають рангом розбиття. Якщ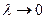о , то 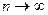(але не навпаки). Сума 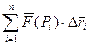залежить від способу розбиття кривої 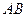й вибору точок 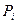. Розглянемо (*).

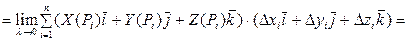
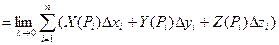Означення. Якщо границя (*) існує, то вона називається криволінійним інтегралом за координатами і позначається .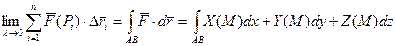

Криву 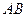називають контуром інтегрування.

Таким чином, робота змінної сили 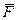під час руху точки по кривій 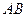дорівнює криволінійному інтегралу

.

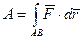Лекція 34

114. Формула зв'язку криволінійних інтегралів за координатами і довжиною дуги

Нехай L - гладка крива, задана вектор-функцією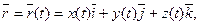

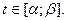
Розглянемо одиничний дотичний вектор

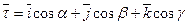, вектор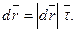

Запишемо теорему пункту 109 через диференціали:

.

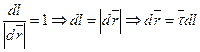Криволінійний інтеграл за координатами

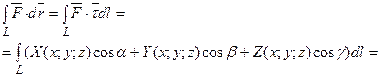
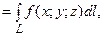тут .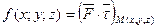

Таким чином, криволінійний інтеграл за координатами 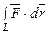існує, якщо існує криволінійний інтеграл за довжиною дуги 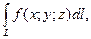й навпаки.

115. Формулювання теореми існування криволінійного інтеграла

Теорема. Якщо 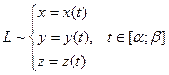- гладка крива, а вектор-функція

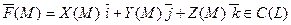, то існує криволінійний інтеграл за координатами , тобто існує границя n-ї інтегральної суми 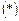(пункт 113), що не залежить від способу розбиття кривої L і вибору точок .

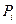Зауваження. Оскільки L - гладка, а F(M)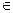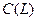, то 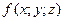теж неперервна на L.

Доведення

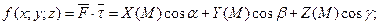
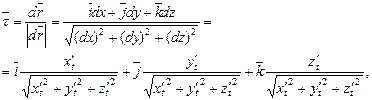
а оскільки крива L гладка, то 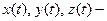неперервно диференційовані й без особливих точок, тобто 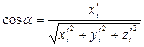, аналогічно 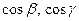- неперервні на L функції.

Отже, .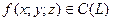

Із зауваження й формули зв'язку випливає, що якщо 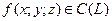й L - гладка, то криволінійний інтеграл за довжиною дуги теж існує.

116. Дві основні властивості криволінійних інтегралів

1. Криволінійний інтеграл за довжиною дуги AB не залежить від вибору напрямку інтегрування, тобто

.

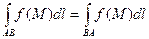Доведення

За означенням

,

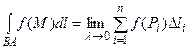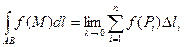
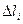- довжина дуги 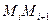не залежить від напрямку її виміру.

2. Криволінійний інтеграл за координатами залежить від вибору напрямку інтегрування, тобто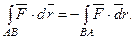

Доведення

За визначенням

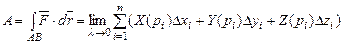
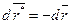
, що й потрібно було довести.

Зауваження. Якщо контур АВ замкнений, то криволінійний інтеграл записують так:

.

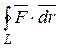117. Обчислення криволінійних інтегралів

Почнемо із криволінійного інтеграла за координатами:

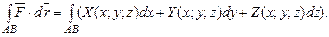
Обчислимо .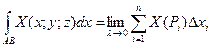

Крива АВ задана рівняннями , .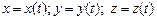

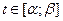За теоремою Лагранжа 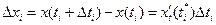, де 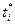лежить між 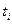і ;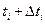

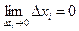, тому що x=x(t) - неперервна.

Оскільки інтеграл не залежить від вибору точок 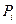(пункт115), то нехай 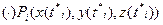, тоді ,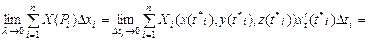

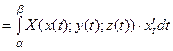тобто криволінійний інтеграл зводиться до визначеного.

Остаточно: .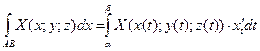

Аналогічно: .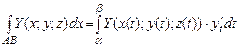

.

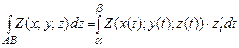З пункту 114 випливає, що метод обчислення криволінійного інтеграла за довжиною дуги такий самий, що й метод обчислення криволінійного інтеграла за координатами.

Оскільки 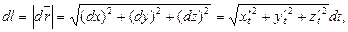то

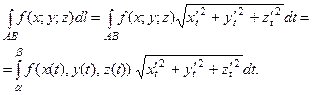
Приклади.

1. 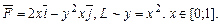Визначити роботу сили .

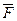Уведемо параметризацію кривої L

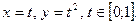
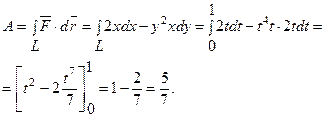
2. Визначити роботу сили 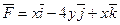під час руху точки М по прямій від точки А(1,0,4) до точки В(7,4,2).

3. Визначити масу параболи 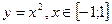, якщо 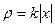- густина.

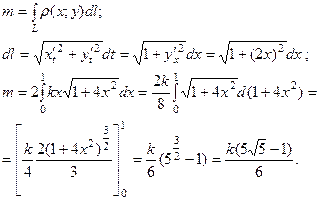
Лекція 35

118. Формула Гріна

Теорема. область 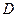правильна уздовж осі й 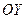, функції , ,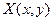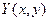