П. 3. Постановка задач для уравнений математической физики

П.2. Примеры уравнений математической физики

П. 1. Классификация дифференциальных уравнений с частными производными

Введение.

Основные уравнения математической физики.

Индекс рентабельности.

Риски в инвестициях.

В инвестиционной деятельности (учитывает инфляцию) возникает 4 вида финансового потока – регулярный финансовый поток в виде серии произвольных платежей.

СF	(1+r) в t	PV ⁿ = СF t (1+r) в t
-100.000	(1+0,1) °=1	-100.000
25.000	1,1 В 1	22.727
30.000	1,21 В 2	24.793
35.000	1,331 В 4	26.296
40.000	1,46 В ³	27.320
45.000	1,61 В 5	27.941
50.000	1,77 В 6	28.223
225.000		157.302

100.000-Инвемтиции, 6 лет получаешь доход

Деньги сегодня намного больше, чем обещанные завтра.

NPV=PV-I0

Net present value

NPV=157302-100000=57302

Если NPV=0, тогда IRR – внутренняя норма доходности

Internal rate of return

IRR= Σ СFt - СF 0 =0

(1+n)в t

NPV=0

IRR-r>0 (2-3%)

25%-10% PV=I0

CF1+CF2 -CF0 =0

(1+0,25) ²

PI – profitability index (индекс доходности)

Benefit

NPV=PV- I0

PI= PV = 157302 =1,57 (дисконтированный доход)

I0 100000

CF0=I0

Дисконтированный доход-доход после вычета инфляции.

Математические задачи, возникающие при изучении различных физических процессов и явлений, содержат много общих элементов и составляют предмет математической физики. Эта отрасль науки и ее методы начали формироваться в XVIII веке при изучении колебаний струны и стержня, при решении задач акустики, гидродинамики и аналитической механики. Новое развитие идеи математической физики получили в XIX веке в связи с задачами теплопроводности, диффузии, упругости, оптики, электродинамики, нелинейными волновыми процессами и теорией устойчивости движения. Круг вопросов, относящихся к математической физике, чрезвычайно широк. В XX веке в нее включаются задачи теории относительности, квантовой физики, новые проблемы газовой динамики, кинетических уравнений, теории ядерных реакторов и физики плазмы.

Постановка задач, связанных с изучением физических проблем, имеет специфические особенности. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов. Основными математическими средствами исследования задач математической физики служат теория дифференциальных уравнений с частными производными, функциональный анализ, численные методы и вычислительная математика.

Уравнение, связывающее неизвестную функцию 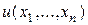, независимые переменные 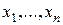и частные производные от неизвестной функции, называется дифференциальным уравнением с частными производными.

Оно имеет вид

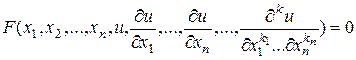, (1.1)

где 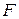– заданная функция своих аргументов.

Порядок старшей производной, входящей в уравнение (1.1), называется порядком уравнения с частными производными.

При решении задач математической физики наиболее часто встречаются дифференциальные уравнения второго порядка.

Решением уравнения с частными производными (1.1) называется всякая функция 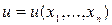, которая, будучи подставлена в уравнение вместо неизвестной функции и ее частных производных, обращает это уравнение в тождество по независимым переменным.

Уравнение с частными производными называется линейным, если оно линейно относительно неизвестной функции и ее частных производных.

Так, например, уравнение

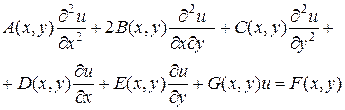(1.2)

есть линейное уравнение второго порядка относительно неизвестной функции 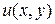, где 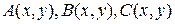– функции, имеющие непрерывные производные до второго порядка включительно и не обращаются одновременно в нуль. Если коэффициенты уравнения (1.2) не зависят от и , то оно представляет собой линейное уравнение с постоянными коэффициентами. Уравнение (1.2) называется однородным, если .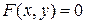

Доказано, что любое дифференциальное уравнение вида (1.2) с помощью преобразования независимых переменных и можно привести к каноническому виду. Дифференциальное уравнение (2) принадлежит:

1. гиперболическому типу, если ;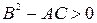

2. параболическому типу,если ;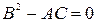

3. эллиптическому типу, если .

Дифференциальные уравнения с частными производными классифицируются и по другому принципу. Одна из независимых переменных искомой функции трактуется как время , а остальные переменные имеют смысл пространственных координат. Если в записи уравнения (1.2) нет переменной , то оно называется стационарным и описывает физические процессы, установившиеся во времени (уравнение эллиптического типа). При наличии в записи уравнения переменной оно описывает процессы, развивающиеся во времени, и называется нестационарным (уравнения гиперболического и параболического типов).

Для каждого типа канонических уравнений разработаны определенные методы как аналитического, так и численного решения.

1. При изучении различных видов волн – упругих, звуковых, электромагнитных, а также других колебательных явлений приходим к уравнению гиперболического типа – волновому уравнению

, (1.3)

2. Процессы распространения тепла в однородном изотропном теле, так же как и явления диффузии, описываются уравнением параболического типа – уравнением теплопроводности

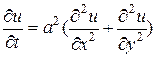, (1.4)

2. Математической моделью установившегося теплового состояния в однородном изотропном теле является уравнение эллиптического типа – уравнение Пуассона:

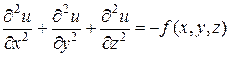. (1.5)

При отсутствии внутренних источников тепла уравнение (1.5) переходит в уравнение Лапласа

. (1.6)

Потенциалы поля тяготения и стационарного электрического поля также удовлетворяют уравнению Лапласа, в котором отсутствуют соответственно массы и электрические заряды.

Уравнения (1.3) – (1.6) часто называют основными уравнениями математической физики. Их подробное изучение дает возможность построить теорию физических явлений разной природы и решить широкий круг инженерно-технических задач.

Каждое из уравнений (1.3) – (1.6) имеет бесчисленное множество частных решений. При решении конкретной физической задачи из всех этих решений необходимо выбрать то, которое удовлетворяет некоторым дополнительным условиям, вытекающим из ее физического смысла. Дополнительные условия, заданные на границе исследуемой области, называются граничными или краевыми условиями. А дополнительные условия, относящиеся к моменту времени, с которого начинается изучение данного физического явления, называются начальными условиями.

Для уравнений эллиптического типа задаются только граничные условия. Для уравнений гиперболического и параболического типов задаются одновременно начальные и граничные условия.

Математическая задача, описывающая реальный физический процесс должна удовлетворять трем требованиям – разрешимости, однозначности и непрерывной зависимости от исходных данных (иначе, устойчивости). Задача, удовлетворяющая этим требованиям, называется корректно поставленной задачей. Соблюдение требований корректности постановок задач математической физики обеспечивает физическую содержательность их решения.

Дата добавления: 2013-12-13