
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы о функциях, непрерывных на отрезке
|
|
|
|
Классификация точек разрыва.
По определению, если функция 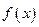 непрерывна в точке
непрерывна в точке 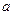 , то существуют и конечны оба односторонних предела
, то существуют и конечны оба односторонних предела 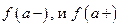 и при этом
и при этом  . В точке разрыва какое-либо из этих условий нарушено.
. В точке разрыва какое-либо из этих условий нарушено.
Говорят, что функция 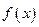 имеет в точке
имеет в точке 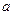 разрыв первого рода, если оба односторонних предела
разрыв первого рода, если оба односторонних предела 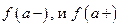 существуют и конечны, но не выполняется хотя бы одно из указанных равенств. В частности,
существуют и конечны, но не выполняется хотя бы одно из указанных равенств. В частности, 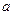 − точка устранимого разрыва, если
− точка устранимого разрыва, если 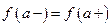 , если же
, если же  , то
, то 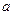 называется точкой скачка; величиной скачка называют разность
называется точкой скачка; величиной скачка называют разность  .
.
Говорят, что функция 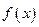 имеет в точке
имеет в точке 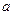 разрыв второго рода, если разрыв в этой точке не относится к первому роду, т.е. пределы
разрыв второго рода, если разрыв в этой точке не относится к первому роду, т.е. пределы  или
или  не существуют или бесконечны. В частности, если хотя бы один из односторонних пределов бесконечен, то функция
не существуют или бесконечны. В частности, если хотя бы один из односторонних пределов бесконечен, то функция 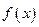 имеет бесконечный разрыв.
имеет бесконечный разрыв.
Примеры
1.  . Эта функция имеет при
. Эта функция имеет при 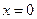 устранимый разрыв, так как
устранимый разрыв, так как 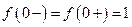 . Для устранения этого разрыва достаточно доопределить эту функцию по непрерывности, положив
. Для устранения этого разрыва достаточно доопределить эту функцию по непрерывности, положив 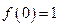 .
.
2.  . Эта функция имеет скачок в каждой целочисленной точке
. Эта функция имеет скачок в каждой целочисленной точке 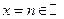 и
и  .
.
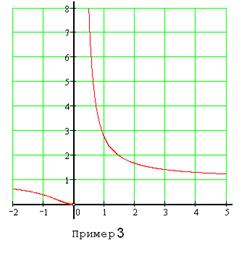
3. 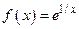 . Здесь
. Здесь  ,
, 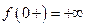 , поэтому 0 − точка бесконечного разрыва.
, поэтому 0 − точка бесконечного разрыва.
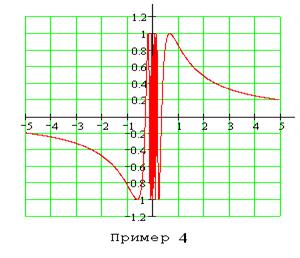
4.  . Так как
. Так как 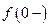 и
и  не существуют, то, как и в предыдущем примере, при
не существуют, то, как и в предыдущем примере, при 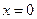 имеем точку разрыва второго рода.
имеем точку разрыва второго рода.

| 
|
| 
|
Определение. Функцию 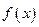 мы будем называть непрерывной на отрезке
мы будем называть непрерывной на отрезке 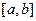 и писать
и писать  (
(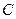 − начальная буква слова continuous − непрерывный), если
− начальная буква слова continuous − непрерывный), если  непрерывна во всех внутренних точках этого отрезка и односторонне непрерывна в его концах, т.е.
непрерывна во всех внутренних точках этого отрезка и односторонне непрерывна в его концах, т.е. 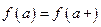 ,
,  .
.
Теорема 1. (Теорема Коши о прохождении через нуль.) Пусть  . Если на концах отрезка
. Если на концах отрезка  принимает значения разных знаков, то
принимает значения разных знаков, то  обращается в нуль внутри отрезка, т.е. если
обращается в нуль внутри отрезка, т.е. если 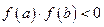 , то
, то  .
.
Доказательство. Пусть, например,  и
и . Мы будем писать дальше
. Мы будем писать дальше 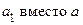 и
и  . Обозначим
. Обозначим  . Если
. Если  , то полагаем
, то полагаем  и доказательство закончено. Если же
и доказательство закончено. Если же 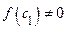 , то из двух отрезков
, то из двух отрезков 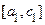 и
и 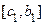 выбираем тот, на концах которого функция
выбираем тот, на концах которого функция  меняет знак. Обозначим концы этого отрезка
меняет знак. Обозначим концы этого отрезка 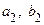 .
.
Ясно, что 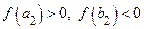 . Обозначим
. Обозначим  . Если
. Если  , полагаем
, полагаем  и считаем, что доказательство закончено. Если
и считаем, что доказательство закончено. Если  , то обозначаем
, то обозначаем 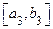 ту половину предыдущего отрезка, где
ту половину предыдущего отрезка, где 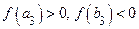 .
.
|
|
|
При продолжении этот процесс либо оборвется из-за того, что одно из чисел  окажется корнем функции
окажется корнем функции  , либо будет построена бесконечная последовательность вложенных стягивающихся отрезков
, либо будет построена бесконечная последовательность вложенных стягивающихся отрезков  таких, что
таких, что  . В точке
. В точке 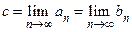 функция
функция  обращается в нуль, т.к.
обращается в нуль, т.к.  и
и 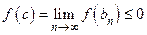 . Доказательство окончено.
. Доказательство окончено.
Следствие. (Теорема Коши о промежуточном значении.) Пусть  . В таком случае
. В таком случае  принимает внутри отрезка все значения, промежуточные между числами
принимает внутри отрезка все значения, промежуточные между числами 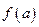 и
и  .
.
Доказательство. Пусть 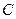 − значение, промежуточное между числами
− значение, промежуточное между числами 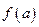 и
и  . Тогда функция
. Тогда функция  удовлетворяет всем условиям теоремы о прохождении через нуль. В таком случае найдется точка
удовлетворяет всем условиям теоремы о прохождении через нуль. В таком случае найдется точка  такая, что
такая, что  , но тогда
, но тогда  .
.
Теорема 2. (Теорема Вейерштрасса о наибольшем значении.) Пусть  . В таком случае
. В таком случае
1) функция 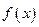 ограниченна на этом отрезке;`
ограниченна на этом отрезке;`
2) функция 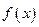 принимает в точках этого отрезка свое наибольшее (и свое наименьшее) значения.
принимает в точках этого отрезка свое наибольшее (и свое наименьшее) значения.
Доказательство пункта 1). Предположим, что функция 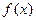 неограниченна сверху. В этом случае для любого натурального
неограниченна сверху. В этом случае для любого натурального 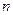 найдется точка
найдется точка 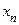 , в которой
, в которой 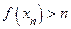 . Теоремы Больцано-Вейерштрасса утверждает, что из этой последовательности можно выделить сходящуюся подпоследовательность
. Теоремы Больцано-Вейерштрасса утверждает, что из этой последовательности можно выделить сходящуюся подпоследовательность  . Пусть
. Пусть  − предел этой подпоследовательности. Тогда, с одной стороны, по свойству локальной ограниченности
− предел этой подпоследовательности. Тогда, с одной стороны, по свойству локальной ограниченности 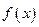 должна быть ограниченной в окрестности точки
должна быть ограниченной в окрестности точки  , а с другой −
, а с другой −  . Полученное противоречие доказывает, что функция
. Полученное противоречие доказывает, что функция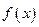 ограниченна сверху. Точно так же доказывается ограниченность
ограниченна сверху. Точно так же доказывается ограниченность 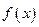 снизу.
снизу.
Доказательство пункта 2). Т.к. множество значений, принимаемых функцией 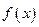 на отрезке
на отрезке  , ограниченно, существует
, ограниченно, существует  . Докажем, что существует такая точка
. Докажем, что существует такая точка  , где
, где  . Если это было бы не так, непрерывная функция
. Если это было бы не так, непрерывная функция  принимала бы только положительные значения. Тогда функция
принимала бы только положительные значения. Тогда функция  была бы непрерывной на отрезке
была бы непрерывной на отрезке 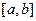 . Согласно пункту 1) существовало бы положительное число
. Согласно пункту 1) существовало бы положительное число  такое, что
такое, что  при всех
при всех 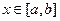 . Но тогда мы бы имели неравенство
. Но тогда мы бы имели неравенство  на отрезке
на отрезке 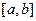 , а этого быть не может, т.к.
, а этого быть не может, т.к.  .
.
|
|
|
Определение. Функция 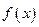 называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве 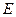 , если
, если  .
.
Ясно, что функция, равномерно непрерывная на промежутке, непрерывна в каждой его точке.
Простейшие контрпримеры показывают, что обратное утверждение не верно.
Контрпримеры: 1).  ; 2).
; 2).  .
.
Теорема 3. (Теорема Кантора о равномерной непрерывности.) Если  , то эта функция равномерно непрерывна на отрезке
, то эта функция равномерно непрерывна на отрезке 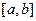 .
.
Доказательство. Предположим противное. Это означает существование  такого, что
такого, что  найдутся значения
найдутся значения  , для которых
, для которых 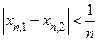 , но
, но  . Ввиду теоремы Больцано-Вейерштрасса можно считать, что обе последовательности
. Ввиду теоремы Больцано-Вейерштрасса можно считать, что обе последовательности 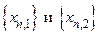 сходятся. Ясно, что они должны иметь один и тот же предел, скажем
сходятся. Ясно, что они должны иметь один и тот же предел, скажем 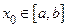 . По условию теоремы функция
. По условию теоремы функция  непрерывна в точке
непрерывна в точке  , следовательно
, следовательно  . А это противоречит тому, что
. А это противоречит тому, что 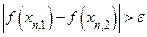 ,
,  .
.
Теорема 4. (Теорема об обратной функции) Если функция 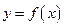 непрерывна и строго возрастает на отрезке
непрерывна и строго возрастает на отрезке 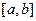 , то на отрезке
, то на отрезке 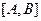 , где
, где  существует обратная к ней функция
существует обратная к ней функция 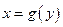 , т.е.
, т.е.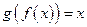 . При этом обратная функция также является непрерывной и строго монотонной.
. При этом обратная функция также является непрерывной и строго монотонной.
Лемма. Если функция 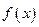 монотонна в окрестности точки
монотонна в окрестности точки  и не пропускает там промежуточных значений, то она непрерывна в этой точке.
и не пропускает там промежуточных значений, то она непрерывна в этой точке.
Доказательство леммы. Слева от точки  функция ограничена сверху числом
функция ограничена сверху числом 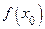 . Поэтому существует
. Поэтому существует  . Точно так же существует предел
. Точно так же существует предел  . При этом для любого,
. При этом для любого,  будет
будет 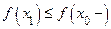 , а для любого
, а для любого  будет
будет 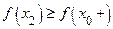 . Отсюда видно, что
. Отсюда видно, что  , иначе, функция
, иначе, функция 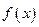 пропускала бы много значений, промежуточных между числами
пропускала бы много значений, промежуточных между числами  . Например, она пропускала бы все числа из объединения интервалов
. Например, она пропускала бы все числа из объединения интервалов  .
.
Доказательство теоремы 4. Так как функция 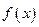 строго возрастает, то отображение
строго возрастает, то отображение  является взаимно однозначным. Отсюда следует существование обратной функции
является взаимно однозначным. Отсюда следует существование обратной функции  , которая также строго монотонна. Функция
, которая также строго монотонна. Функция  не пропускает промежуточных значений, так множество принимаемых ею значений совпадает с отрезком
не пропускает промежуточных значений, так множество принимаемых ею значений совпадает с отрезком  . Согласно лемме функция
. Согласно лемме функция  непрерывна на множестве
непрерывна на множестве 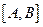 .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1010; Нарушение авторских прав?; Мы поможем в написании вашей работы!