Для вычисления интегралов вида , где − рациональная функция двух переменных, можно использовать подстановки Эйлера

Интегрирование квадратичных иррациональностей.

I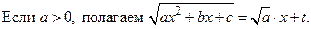

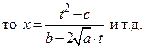
II.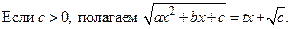Тогда будет 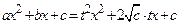или

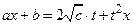, следовательно, и т.д.

III Если дискриминант квадратного трёхчлена 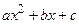больше нуля, то трёхчлен можно разложить на линейные множители: . В этом случае применима третья подстановка Эйлера: или (см. пункт 1˚).

Отметим, что в случае, когда 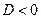, будет 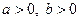и можно использовать любую из первых двух подстановки.

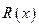2. Если не пользоваться подстановками Эйлера, интегралы от квадратичных иррациональностей можно ещё привести к виду , где − рациональная функция одной переменной. Дробь 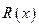можно представить в виде суммы алгебраического многочлена и простых дробей. Поэтому задача интегрирования сводится к вычислению подобных интегралов с заменой 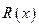на алгебраический многочлен или простую дробь.

В первом случае удобно использоватьследующий приём.

Метод Остроградского:

.

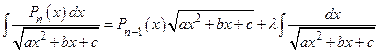Здесь 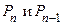− алгебраические многочлены степени, соответственно. Коэффициенты многочлена и число подбирают с помощью метода неопределённых коэффициентов.

Для вычисления интегралов можно использовать подстановку 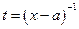. Оставшиеся интегралы с помощью дробно-линейной подстановки приводятся к виду , а к этому интегралу можно применить подстановку Абеля .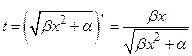

Пример 3. Вычислить интеграл .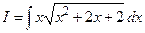

1-й способ. Подстановка Эйлера . Она приводит к сложным выкладкам.

2-й способ. . Дифференцируя это соотношение и домножая затем , приходим к равенству 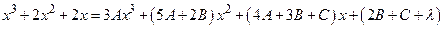. Это приводит к системе линейных уравнений

. Решая систему, находим 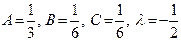. Следовательно,

.

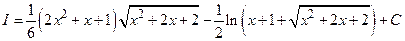3-й способ. 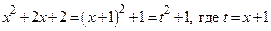. После этой подстановки получаем

.

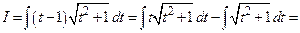
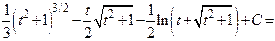
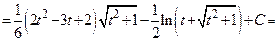
Другие способы. Для вычисления интеграла можно также воспользоваться подстановками .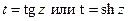

Пример 4. Вычислить интеграл .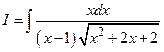

Прежде всего, .
Для вычисления интеграла делаем замену . Тогда будет

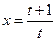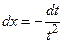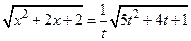, , или .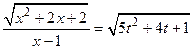

Поэтому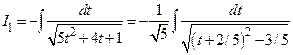

.

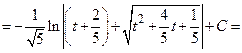
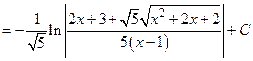Пример 5. Вычислить интеграл .

Воспользуемся подстановкой Абеля . Мы имеем и . С другой стороны, . Дифференцируя это равенство, получаем или 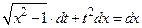. Отсюда следует, что 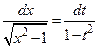. Поэтому 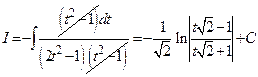. Окончательно получаем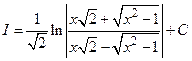

Дата добавления: 2013-12-13