
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В.7. Непрерывность функции
|
|
|
|
В. 6. Замечательные пределы
Первым замечательным пределом является:
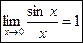
Вторым замечательным пределом является:
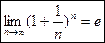
где е» 2,718281 … –число Эйлера, которое является основанием для натуральных логарифмов. Этот предел имеет записи:
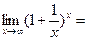 е или
е или 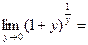 е.
е.
Пример 2. 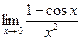
Для раскрытия подобных неопределенностей 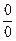 используется первый замечательный предел:
используется первый замечательный предел: 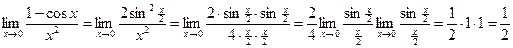
Пример 3. 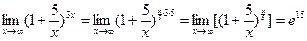
Пример 4. 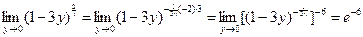
Функция f (x) называется непрерывной в точке х0, если она удовлетворяет следующим условиям:
1) она определена в точке х0,, т.е. существует f(х0);
2) она имеет конечный предел функции при х ® х0 (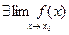 );
);
3) этот предел равен значению функции в точке х0, т.е.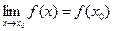
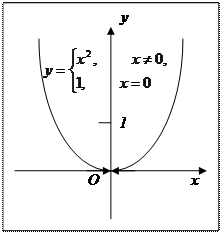
Пример 6. А) Функция 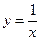 в точке х = 0 не является непрерывной (нарушено 1-е условие).
в точке х = 0 не является непрерывной (нарушено 1-е условие).
Б) Функция, заданная выражением: 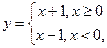 в точке х = 0 не является непрерывной из-за отсутствия предела при х ® 0, хотя существуют пределы слева и справа (нарушено 2-е условие).
в точке х = 0 не является непрерывной из-за отсутствия предела при х ® 0, хотя существуют пределы слева и справа (нарушено 2-е условие).
В) 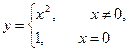 - не является непрерывной, т.к. нарушено 3-е условие.
- не является непрерывной, т.к. нарушено 3-е условие.
Г) Функция y = x2 является непрерывной в точке х = 0.
|
  y
1_ y
1_ 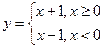
 x x
 1_ 1_
| 
|
Непрерывность функции f (x) в точке х0 можно записать и так:
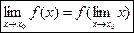
т.е. для непрерывной функции возможна перестановка символов предела и функции.
Другое определение непрерывности: функция y = f (x) называется непрерывной в точке х0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 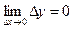
Оба определения равносильны.
Точка х0 называется точкой разрыва функции f (x), если эта функция в данной точке не является непрерывной. Существует две разновидности точек разрыва.
Точка разрыва 1-го рода: существуют конечные односторонние пределы функции слева и справа при х ® х0, не равные друг другу.
|
|
|
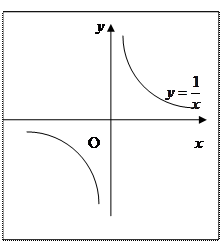
В качестве примера можно указать точку х = 0 для функции 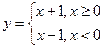 .
.
Точка разрыва 2-го рода: хотя бы один из односторонних пределов равен бесконечности или не существует.
В качестве примера можно указать точку х = 0 для функции 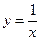 .
.
Свойства функций непрерывных в точке:
1. Если функции f (x) и j (х) непрерывны в точке х0, то их сумма f (x) + j (х), произведение f (x) × j (х) и частные 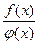 (j (х) ¹ 0) являются функциями, непрерывными в точке х0 .
(j (х) ¹ 0) являются функциями, непрерывными в точке х0 .
2. Если функция y = f (x) непрерывна в точке х0 и f(x0) > 0, то существует такая окрестность точки x0, в которой и f(x) > 0.
3. Если функция y = f (u) непрерывна в точке u0 и f(x0) > 0, а функция u = j (х) непрерывна в точке х0, то сложная функция y = f [ j (х)] непрерывна в точке х0 .
Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.
Свойства функций непрерывных на отрезке:
1. Если функция y = f (x) непрерывна на отрезке [ a, b ], то она ограничена на этом отрезке.
2. Если функция y = f (x) непрерывна на отрезке [ a, b ], она достигает на этом отрезке наименьшего значения m и наибольшего значения M.
3. Если функция y = f (x) непрерывна на отрезке [ a, b ] и ее значения на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка x Î (a, b) такая, что f (x)=0.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 300; Нарушение авторских прав?; Мы поможем в написании вашей работы!