Конечные автоматы

Регулярные определения

Для удобства записи регулярным выражениям можно давать имена и определять другие регулярные выражения с использованием этих имен так, как если бы эти имена были отдельными символами.

Если 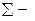алфавит, то регулярное определение представляет собой последовательность вида:

,

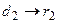
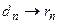где каждое 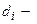индивидуальное имя, а каждое регулярное выражение над символами из 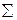и уже определенными именами, т.е. над символами из .

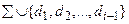Пример.

Множество идентификаторов в языке программирования – это множество строк из букв и цифр, начинающихся с буквы. Вот регулярное определение этого множества:

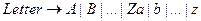
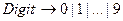
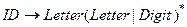
Распознавателем языка называется программа, которая получает на вход строку 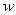и отвечает «да», если 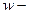строка языка, «нет» - в противном случае.

Недетерминированный конечный автомат (НКА) представляет собой математическую модель, состоящую из пяти элементов:

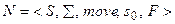, где

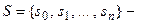1. конечное множество состояний (алфавит состояний);
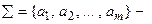2. конечное множество входных символов (входной алфавит);
3. функция переходов, которая отображает пары «символ, состояние» в некоторое подмножество состояний, т.е.
   
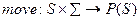
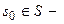4. начальное состояние (стартовое состояние);
5. подмножество заключительных (допускающих) состояний.

Пример. Конечный автомат, распознающий регулярное выражение , может быть представлен в виде:

1. ;
2. ;
3. 

1. 
2. 

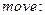
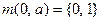
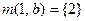
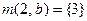
НКА может быть представлен в виде графа переходов.

Вершины в таком графе – это состояния автомата. Помеченные дуги представляют функцию переходов, входной алфавит – символы на дугах. Начальное состояние – вершина, на которую указывает стрелка, не имеющая начала. Заключительные состояния – вершины, отмеченные двойным кружком.

Пример.

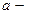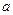НКА может быть представлен в виде таблицы переходов. В такой таблице: строки – состояния КА, столбцы – входные символы. Запись в строке для символа подмножество состояний, которые могут быть достигнуты из состояния при входном символе . Строка, соответствующая начальному состоянию, отмечена стрелкой. Строки, соответствующие заключительным состояниям, отмечены «*».

	a	b
-> 0	{0, 1}	{0}
	Ø	{2}
	Ø	{3}
* 3	Ø	Ø

НКА допускает (принимает) входную строку 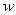тогда и только тогда, когда в графе переходов существует некоторый путь из начального состояния к какому-либо из заключительных состояний, такой, что метки на дугах этого пути соответствуют строке .

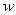Путь может быть представлен в виде последовательности переходов из текущего состояния в другое состояние.

Пример. .

Язык, определяемый НКА, представляет собой множество допускаемых им входных строк.

Детерминированный конечный автомат (ДКА)

ДКА – это частный случай НКА, в котором:

отсутствуют состояния, имеющие переходы;

для каждого состояния 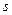и входного символа 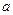существует не более одной дуги, исходящей из 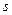и помеченной как .

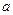ДКА

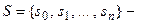1. конечное множество состояний (алфавит состояний);
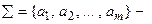2. конечное множество входных символов (входной алфавит);
3. функция переходов, которая отображает пары «символ, состояние» в некоторое подмножество состояний, т.е.
   
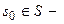4. начальное состояние (стартовое состояние);
5. подмножество заключительных (допускающих) состояний.

Дата добавления: 2013-12-14