
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие о геоиде, квазигеоиде, земном эллипсоиде
|
|
|
|
Геоид, квазигеоид и общий земной эллипсоид – это три модели Земли. Дадим их определения с точки зрения современных представлений о фигуре Земли.
Под фигурой Земли в настоящее время понимают фигуру, ограниченную физической поверхностью Земли, т.е. поверхностью ее твердой оболочки на суше и невозмущенной поверхностью морей и океанов.
Суша составляет третью часть от земной поверхности и в среднем она возвышается над водой примерно на 900 метров, что незначительно по сравнению с радиусом Земли (6371км). Поэтому за фигуру Земли в первом приближении принят геоид.
Дадим два определение геоид:
1. Строгое: геоид – это уровенная поверхность поля силы тяжести Земли, проходящая через начало счета высот.
2. Нестрогое: геоид – это фигура, ограниченная невозмущенной поверхностью морей и океанов и продолженная под материками так, чтобы отвесные линии во всех ее точках были перпендикулярны к ней.
Более ста лет, т. е. с первой половины прошлого века геодезисты и геофизики изучали фигуру геоида и считали это основной научной задачей высшей геодезии. В середине прошлого столетия советским ученым Молоденским было доказано, что фигура геоида, строго говоря, неопределима. Он предложил основной задачей высшей геодезии считать изучение фигуры реальной Земли и ее гравитационного поля. Молоденский создал теорию, которая позволяет точное определение фигуры Земли на основании выполненных на земной поверхности измерений, без привлечения каких – либо гипотез об ее внутреннем строении.
В теории Молоденского в качестве вспомогательной вводится поверхность квазигеоида, совпадающая с геоидом на океанах и морях и весьма мало отступающая от поверхности геоида на суше (менее 2м).
В отличие от геоида поверхность квазигеоида может быть строго определена по результатам наземных наблюдений.
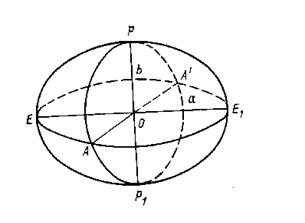
С понятием земного эллипсоида мы уже столкнулись при рассмотрении главной научной задачи высшей геодезии. Напомню, что поверхность земного эллипсоида является той математически и геометрически простой поверхностью, на которой могут быть решены геодезические задачи по координированию точек земной поверхности и которая достаточной близка к поверхности Земли. Земной эллипсоид представляет собой эллипсоид вращения с малым полярным сжатием. Его поверхность может быть получена вращением полуэллипса РЕР1 вокруг его малой оси РР1 (рис 1.2).
|
Рис. 1.2. К понятию земного эллипсоида: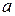 — большая полуось; b — малая полуось.
— большая полуось; b — малая полуось.
Поверхность земного эллипсоида в геодезии принимают за отсчетную, определяя относительно нее высоты точек поверхности изучаемой фигуры Земли.
Форма и размеры земного эллипсоида характеризуются большой и малой полуосями 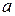 и b, а чаще большой полуосью
и b, а чаще большой полуосью 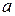 и полярным сжатием
и полярным сжатием 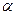
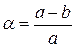 (1.1)
(1.1)
или большой полуосью 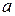 и эксцентриситетом
и эксцентриситетом 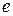 меридианного эллипса:
меридианного эллипса:
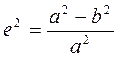
 (1.2)
(1.2)
Эллипсоид, имеющий наибольшую близость к фигуре Земли в целом, называется общим земным эллипсоидом.
Параметры общего земного эллипсоида определяются под условиями:
1) центр эллипсоида должен совпадать с центром масс Земли, а его малая ось с осью вращения Земли1;
2) объем эллипсоида должен быть равен объему геоида (квазигеоида);
3) cумма квадратов отклонений по высоте поверхности эллипсоида от поверхности геоида (квазигеоида) должна быть минимальной.
Параметры земного эллипсоида могут быть получены с помощью так называемых градусных измерений, заключающихся в проложении рядов триангуляции по направлениям меридианов и параллелей на разных широтах с определением на конечных пунктах астрономических широт, долгот и азимутов сторон, а также по результатам спутниковых наблюдений.
В течение полутора веков ученые разных стран занимались определением параметров земного эллипсоида, используя доступные им результаты градусных измерений. Итогом этих определений служит появление ряда эллипсоидов, наиболее известные из которых представлены в таблице 1.1.
Таблица 1.1.
Параметры наиболее известных земных эллипсоидов
| Ученый | Государство | Год | 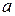 , м , м
| 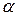
|
| Деламбр Бессель Кларк Хейфорд Красовский | Франция Германия Великобритания США СССР | 6 375 653 6 377 397 6 378 206 6 378 388 6 378 245 | 1/334.0 1/299.2 1/294.98 1/297 1/298.3 | |
| Эллипсоиды, полученные по результатам спутниковых наблюдений | 1984 (WGS84) | 6 378 137 6 378 137 | 1/298.257 1/298.257220 |
1имеется в виду среднее положение центра масс и оси вращения в теле Земли.
В каждой стране принимают в качестве рабочего тот эллипсоид, который наилучшим образом подходит для ее территории. В соответствии с этим критерием выполняют и его ориентирование на теле Земли, т.е. определение координат начального пункта. Такие рабочие эллипсоиды, используемые в разных странах, называются референц - эллипсоидами. В СССР и ряде стран восточной Европы принят референц - эллипсоид Красовского, 1940г. Эллипсоид Красовского является наиболее точным из всех эллипсоидов, полученных из обработки наземных измерений. Его размеры близки к размерам ОЗЭ, найденным по данным наблюдений ИСЗ.
1.3. Основные разделы высшей геодезии; связь дисциплины с другими
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 6259; Нарушение авторских прав?; Мы поможем в написании вашей работы!