Основная теорема матричных игр

Основная теорема матричных игр (теорема Д. фон Неймана) утверждает, что каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий, то есть всегда имеет место равенство

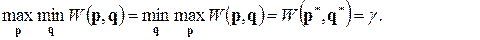(4.2.1)

Смешанные стратеги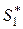и и , удовлетворяющие равенству (4.2.1) называют оптимальными (они образуют ситуацию равновесия), а величину γ ―средний результат игры при использовании оптимальных смешанных стратегий называют ценой игры.

Если оба игрока используют свои оптимальные смешанные стратегии, то

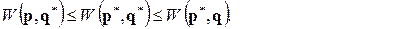(4.2.2)

Для того, чтобы в матричной игреситуацияв смешанных стратегиях 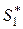и была ситуацией равновесия, необходимо и достаточно, чтобы условие (4.2.2) выполнялось не для всех возможных смесей активных чистых стратегий, а только для всех чистых стратегий игроков 1 и 2.

Если один из игроков использует свою оптимальную смешанную стратегию, то его средний выигрыш(проигрыш) остается неизменным и равным цене игры γ независимо от того, какой смесью активных чистых стратегий пользуется другой игрок.

В частности, средний выигрыш игрока 1 (средний проигрыш игрока 2) остается неизменным и равным цене игры γ при использовании игроком 2 (игроком 1) любой чистой стратегии.

Докажем это для игры m × n. Пусть решение игры , 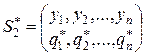. Обозначим γ ₁, γ ₂,…, γ_n выигрыши игрока 1 при использовании игроком 2 чистых стратегий y ₁, y ₂,…, y_n.

Из определения оптимальной стратегии следует, что любое отклонение игрока 2 от стратегии не может быть ему выгодно, поэтому его проигрыши γ ₁ ≥ γ, γ ₂ ≥ γ,…, γ_n ≥ γ. Но возможно ли это? Поскольку в стратегии чистые стратегии y ₁, y ₂,…, y_n применяются с частотами q ₁, q ₂,…, q_n, то средний проигрыш игрока B (цена игры)

(4.2.3)

Очевидно, что если хотя бы одна из величин γ ₁, γ ₂,…, γ_n больше γ, то есть равна γ+∆γ, а другие равны γ, то это противоречит системе (4.2.3). Таким образом, доказано свойство оптимальных смешанных стратегий.

Итак, все сказанное справедливо, если игровая ситуация повторяется многократно в сходных условиях и осреднение результатов игр допустимо; каждый игрок не имеет информации о конкретном, хотя и случайном выборе стратегии другим игроком. Если же игрок 2 информирован о действиях игрока 1, то есть знает его конкретную стратегию x_i в каждом повторении игры, то средний выигрыш игрока 1 при использовании им смешанной стратегии может оказаться меньше гарантированной при максиминной чистой стратегии нижней цены игры α. В этом случае игрок 2 наказывает игрока 1 за отклонение от максиминной чистой стратегии.

Дата добавления: 2013-12-13