Множественный регрессионный анализ

Матричный метод решения парной регрессии.

Парное линейное уравнение регрессии может быть записано в матричной форме: У= ВХ + Е, где

У – вектор-столбец размерности (n × 1) фактических значений результативного признака;

В – вектор-столбец размерности (2 × 1) подлежащих оценке параметров модели, т.е. коэффициента регрессии b₁ и свободного члена (параметр а в уравнении );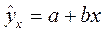

Х = (х ₀, х ₁) – матрица размерности (n × 2) значений факторов. При этом х ₀= 1 и связано с наличием в уравнении регрессии свободного члена, а х ₁– соответственно реальные значения включенного в уравнение регрессии фактора;

Е – вектор столбец случайной величины 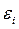размерности (n × 1).

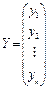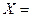
Матрица исходных данных имеет вид: , 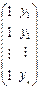. Найдем вектор В и вектор случайной компоненты Е, т.е. 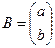или , .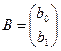

В матричной форме МНК запишется так:

S = (У– ХB) ^Т · (У– ХB) → min

Дифференцируя S по вектору В и приравняв первые частные производные по В к нулю, получим: В = (Х ^ТХ)^–1(Х ^ТУ).

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим, часто возникает задача исследования зависимости одной зависимой переменной y от нескольких объясняющих переменных x ₁, x ₂,..., x _n. Эта задача решается с помощью множественного регрессионного анализа.

Обозначим i -ое наблюдение зависимой переменной y_i , а объясняющие переменные - x_{i 1}, x_{i 1},..., x_{i p}. Тогда модель множественной регрессии можно представить в виде:

y_i = β ₀ + β ₁ x_{i 1} +β ₂ x_{i 1} +... + β _p x_{i p} + ε _i (1)

Где 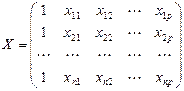- матрица значений объясняющих переменных, или матрица плана размера n× (p +1);

ОЦЕНКА ПАРАМЕТРОВ КЛАССИЧЕСКОЙ РЕГРЕССИОННОЙ МОДЕЛИ

МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Для оценки вектора неизвестных параметров β применим МНК.

Так как e ^Т е = (e ₀ e ₁... e _n) · 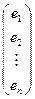= e ₀² + e ₁² +...+ e _p = 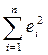, то условие минимизации остатков суммы квадратов запишем в виде:

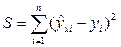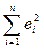= = e ^Т е = (У– Хb) ^Т · (У– Хb) → min

Для нахождения экстремума найдем частные производные и приравняем их к нулю, откуда получаем систему нормальных уравнений в матричной форме для определения b, откуда b = (X^TY)^–1X^TY.

На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда они выражаются разными ед. измерения. В этом случае используют стандартизированные коэффициенты регрессии 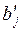и коэффициенты эластичности Еj (j = 1, 2, 3,...): ; .

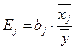Стандартизированный коэффициент регрессии 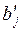показывает на сколько величин S_y изменится в среднем зависимая переменная У при увеличении только j -ой переменной на S_xj ; а коэффициент эластичности Еj – на сколько % (от средней) измениться в среднем У при увеличении только Х j на 1%.

Дата добавления: 2013-12-14