Математическая постановка целочисленных задач линейного программирования

ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Лекция 12

Изучаемые вопросы:

1. Математическая постановка целочисленных задач линейного программирования.

2. Методы отсечения.

3. Обобщенная схема алгоритма Гомори.

Многие экономические задачи характеризуются тем, что объёмы управляемых ресурсов (в силу тех или иных объективных свойств) могут принимать только целые значения. Математическая формализация данных ситуаций приводит к моделям дискретного программирования. В общем виде задача дискретного программирования может быть сформулирована как задача нахождения максимума (или минимума) целевой функции 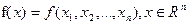на множестве D допустимых решений, определяемом системой ограничений:

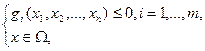
где Ω – некоторое конечное или счётное множество. Условие x Ω называется условием дискретности. Особое место среди дискретных задач занимает целочисленная задача линейного программирования в канонической форме

где – множество неотрицательных целых чисел,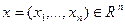. Заметим, что в некоторых ситуациях требование целочисленности может быть наложено лишь на некоторые переменные x_j, что координально не меняет характера задачи.

Принципиальная сложность, вызываемая наличием условия целочисленности в системе ограничений оптимизационной задачи, состоит в том, что в значительном количестве случаев невозможно заменить дискретную задачу её непрерывным аналогом и, найдя соответствующее решение, округлить его компоненты до ближайших целых значений (например, при округлении оптимального плана обычной задачи ЛП до целых значений может получиться точка, не принадлежащая области допустимых решений D. Если даже оптимальный план непрерывной задачи, округлённый до целых значений компонент, окажется допустимым, то целевая функция может вести себя так, что её значение будет на нём существенно хуже, чем на оптимальном плане целочисленной задачи.

Эти проблемы предопределили необходимость разработки специальных методов решения дискретных и целочисленных задач. Как правило, выделяют следующие классы дискретных задач:

- задачи с неделимостями;

- экстремальные комбинаторные задачи;

- задачи с разрывными целевыми функциями;

- задачи на несвязных и невыпуклых областях и др.

Задачи целочисленного линейного программирования занимают важное место среди практически важных задач. Приведём примеры таких задач.

Задача о назначениях. Имеется n видов различных работ и n кандидатов для их выполнения. Предполагается, что каждый кандидат назначается на один и только один вид работы. Обозначим через доход, получаемый при назначении i-того кандидата на j-тый вид работы. Необходимо распределить кандидатов на работу так, чтобы суммарный доход от произведённых назначений был максимальным.

Положим

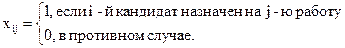
Тогда математическая модель задачи о назначениях примет следующий вид:

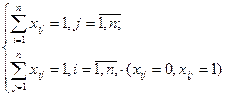
Задача о ранце.

Имеются различные предметы n наименований. Путешественник, собираясь в поход, должен упаковать некоторые из них в ранец. Ранец имеет m ограничений по весу, объёму, линейным размерам и т. п. Пусть - i-тая характеристика предмета j-того наименования 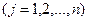; b_i – ограничения по весу, объёму, линейным размерам и т.д.. Пусть – количество предметов j-того наименования, запланированных к загрузке в ранец, а 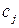– полезность одного предмета j-того наименования. Тогда математическая постановка задачи приобретает следующий вид:

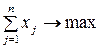
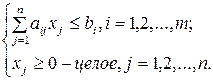
Первоначально в формулировке данной задачи речь шла не о рюкзаке, а о загрузке бомбардировщиков различных типов бомбовым запасом с целью максимизации суммарного эффекта данной системы боевых операций.

Задача о выборе типа судов (или других транспортных средств). Речное пароходство обслуживает n маршрутов с примерно постоянным количеством пассажиров на каждом. Расходы пароходства для обслуживания каждого из m его судов определяются содержанием обслуживающего персонала на каждом судне расходом горючего, доходы - количеством проданных билетов.

Возникает задача о выборе для каждого маршрута судов таких типов и в таких количествах, чтобы перевезти всех пассажиров и максимизировать прибыль пароходства.

Пусть по j-му маршруту за сезон перевозится ⁾ человек. Перевозку пассажиров по этому маршруту можно осуществлять m различными типами судов. Для каждого i-го типа судов известны следующие характеристики:

1). – грузоподъёмность (количество мест);

2). 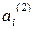– численность обслуживающего персонала;

3). 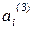– расход горючего за сезон;

4). 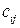– прибыль за сезон от использования i-того судна по j-му маршруту. Необходимо выбрать парк судов для каждого маршрута, при котором максимизируется прибыль пароходства при соблюдении ограничений: общий расход горючего за сезон не может превышать b₃ единиц, а общая численность обслуживающего персонала – b₂ человек.

Математическая модель задачи целочисленного программирования (в стандартной форме) имеет вид:

Найти вектор

минимизирующий линейную функцию:

Дата добавления: 2013-12-13