Нелінійне програмування

Як вже наголошувалося, математичне формулювання завдання оптимізації зводиться до відшукання найбільшого або найменшого значення функції декількох змінних

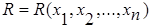(2.12)

за наявності обмежень на оптимізуючі змінні, записаних у вигляді рівностей або нерівностей

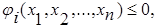
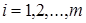. (2.13)

У тих випадках, коли аналітичний вид співвідношень (2.12) і (2.1З) відомий, для знаходження екстремуму можуть бути використані описані вище методи.

Проте при рішенні великого числа практичних завдань доводиться стикатися з випадком, коли вираз (2.12) цільової функції не може бути записаний в явному вигляді при заданій сукупності значень оптимізуючих змінних 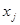. Наявність обмежень (2.13), які можуть бути виражені важковираховуваними функціями, ще більш ускладнює знаходження оптимального рішення. Рішення такого роду завдань з нелінійними і важковираховуваними співвідношеннями, що визначають критерій оптимальності і обмеження на змінні, здійснюється методами нелінійного програмування. Як правило, завдання нелінійного програмування вирішуються тільки чисельними методами, що можливо практично тільки при використанні ЕОМ.

Методи нелінійного програмування є методами послідовного поліпшення початкового рішення, або багатокрокові методи. При цьому в завданнях нелінійного програмування зазвичай заздалегідь не можна сказати, яке число кроків гарантує знаходження оптимуму із заданим ступенем точності. Розроблена велика кількість різноманітних методів нелінійного програмування, які за способом визначення кроку пошуку підрозділяються на безградієнтні і градієнтні методи пошуку оптимуму.

При вирішенні конкретних задач оптимізуючі змінні можуть мати різний фізичний сенс (наприклад, температура, тиск, витрата якого-небудь середовища і т.п.) і відповідно різні одиниці вимірювання. При використанні чисельних методів рішення виявляється доцільним приведення змінних до безрозмірного нормалізованому вигляду.

Для нормалізації їх на основі фізичних уявлень встановлюються можливі діапазони зміни змінних. Допустимо, що деяка фізична величина може міняти своє значення в межах 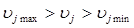. Тоді в безрозмірній нормалізованій формі ця змінна може бути представлена таким чином:

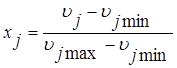, (2.14)

при цьому межа зміни новій нормалізованій змінній буде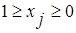

Безградієнтні методи пошуку оптимуму. Безградієнтними методами пошуку екстремуму цільової функції називаються такі, в яких в процесі пошуку використовується порівняльна оцінка величини критерію оптимальності в результаті виконання чергового кроку.

Метод сканування. Цей метод полягає в послідовному обчисленні значення цільової функції у ряді крапок, що належать області зміни оптимізуючих змінних і знаходженні серед цих крапок такий, в якій цільова функція досягає свого екстремального значення. Точність методу сканування залежить від того, наскільки часто розташовуються вибрані крапки в області зміни оптимізуючих змінних.

Достоїнствами методу сканування є те, що його застосування гарантує відшукання глобального екстремуму, а також незалежність пошуку від вигляду функції, що оптимізується. Недоліком є необхідність обчислення значень цільової функції для великого числа крапок.

Додаткові обмеження на незалежні змінні не ускладнюють, а навпаки, спрощують застосування методу сканування, оскільки крапки, що не задовольняють заданим умовам, просто виключаються з розгляду і цільова функція для них не розраховується. Кількість розрахунків, які повинні бути проведені для знаходження екстремуму, визначаються з наступних міркувань.

Якщо задана точність визначення екстремуму ∆, тобто якщо знайдені значення нормалізованих змінних не повинні відрізнятися від дійсного положення оптимуму більше, ніж на величину ∆, то загальне число значень цільової функції, що розраховуються, складе

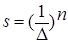
де n - число оптимізуючих змінних (розмірність) вирішуваного завдання.

Так, для відшукання оптимуму функції два змінних R(x1, x2) з точністю ∆ = 1∙10^-3 потрібно буде виконати , а для функції трьох змінних 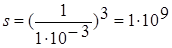розрахунків.

Степенева залежність числа розрахунків від розмірності завдання обмежує ефективне використання методу сканування або завданнями невисокої розмірності, або невисокою точністю пошуку екстремуму.

Для зменшення числа розрахунків існують алгоритми зі змінним кроком сканування, коли спочатку виконується грубий пошук, що дозволяє виявити область знаходження глобального екстремума, а потім, в межах цієї області, здійснюється пошук з меншим кроком.

Метод почергової зміни змінних. Цей метод, відомий також як метод Гаусса-Зейделя, зводиться до зміни в довільній послідовності значення оптимізуючих змінних. Зміна кожній змінній проводиться до тих пір, поки не буде досягнуто екстремальне значення (максимум або мінімум) критерію оптимальності. Після того, як досягнутий оптимум по даній змінній, починається варіювання наступної.

Недоліком цього методу є трудність пошуку за наявності обмежень на значення оптимізуючих змінних або за наявності "ярів" у функції, що оптимізується (яром називається особливість цільової функцій, що полягає в тому, що від певних оптимізуючих змінних функція залежить дуже слабо).

Сімплексний метод. Всі безградієнтні методи пошуку оптимуму пов'язані з виконанням великого числа розрахунків. Для скорочення числа розрахунків і визначення напряму пошуку оптимуму був розроблений сімплексний метод. Ідея цього методу полягає в тому, що по відомих значеннях цільової функції у вершинах опуклого многогранника, названого симплексом, знаходиться напрям, в якому треба зробити наступний крок, щоб отримати найбільшу зміну (збільшення або зменшення) критерію оптимальності.

Поняття симплекс в n- мірному просторі характеризує опуклий многогранник, що має n+1 вершин, кожна з яких утворюється перетином n гіперплощин даного простору.

Прикладом симплексу в двомірному просторі (n=2) являєтся трикутник, а в тривимірному просторі (n=3) – будь-яка чотиригранна піраміда, що має чотири вершини. Симплекс володіє однією властивістю, яка і дала можливість використовувати його для проведення оптимізаційних розрахунків: проти будь-якої його вершини розташована тільки одна грань, на якій можна побудувати новий симплекс що відрізняється від колишнього розташуванням нової вершини , тоді як решта всіх вершин співпадатиме. При цьому нова вершина може знаходитися по іншу сторону грані від вершини .

Пошук оптимуму (мінімуму) функції двох змінних сімплексним методом показаний на рис.2.12. Проводиться розрахунок значень цільової функції в точках , відповідних початковому положенню симплексу (трикутника). Із знайдених трьох значень цільової функції вибирається найбільше. У данному розглядуваному випадку найбільшим значенням буде . Після цього будується новий симплекс : з вершини на протилежну сторону опускається перпендикуляр і на продовженні прямої 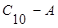відкладається відрізок . Штрихова лінія із стрілкою показує перетворення симплексу. У новій вершині 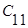обчислюється значення цільової функції і порівнюється із значеннями для інших вершин 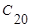і . Потім знаходиться вершина, що відповідає найбільшому значенню цільової функції () і будується наступний симплекс і т.д.

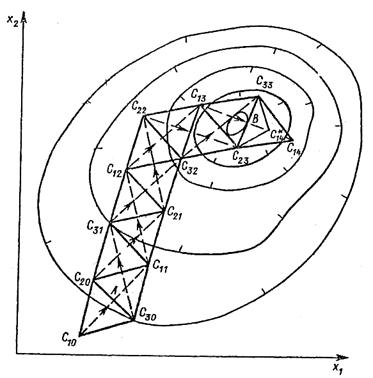
В результаті виключення вершин симплексу з максимальним значенням цільової функції процес направлений до шуканої точки з її мінімальним значенням. На рис.2.12 показано, що поблизу точки екстремуму може відбутися зациклення рахунку, викликане тим, що вершини і матимуть максимальне значення цільовой функції в симплексах і 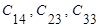. Тоді від симплексу здійснюватиметься перехід до симплексу 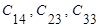, а від останнього – знову до симплексу . Для усунення зациклення необхідно зменшити крок спуску в районі оптимуму. Для цього на продовженні прямої 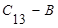повинен бути відкладений не відрізок ,а відрізок . В результаті в симплексі найбільше значення цільової функції буде вже у вершині . Критерієм закінчення пошуку служать розміри симплексу. Пошук оптимуму припиняється, якщо всі ребра симплексу стануть менші наперед заданої, достатньо малої величини.

Як початковий симплекс краще всього використовувати правильний симплекс зі всіма вершинами і гранями, однаково віддаленими від центру (у розглянутому двомірному завданні – рівносторонній трикутник).

Градієнтні методи пошуку оптимуму. У основу градієнтних методів покладено обчислення і аналіз похідних цільової функції.

Коли аналітичний вид цільової функції (2.12) відомий, обчислення похідних () не складає особливих труднощів, хоча у ряді випадків і призводить до вельми громіздких виразів. Якщо ж залежність (2.12) не може бути отримана в явному вигляді або вид цієї залежності виявляється настільки складний, що аналітичні вирази для похідних виявляються дуже громіздкими для практичного використання при розрахунках, то єдиним способом визначення похідних являється чисельний метод. В цьому випадку значення похідної визначається по наближеному співвідношенню

(2.15)

Дата добавления: 2013-12-14