Статистичні ігри з одиничним не ідеальним експериментом

Розглянемо доволі загальний випадок, коли результат одиничного експерименту випадковий і залежить від появи одного з k несумісних подій S₁,S₂, …,S_k, що створюють повну систему подій. Окремі випадки закінчення експерименту пов’язані із станами природи П₁, П_2, ..., П _п. Цей зв’язок проявляється в тому, що для кожного можливого стану природи є певна ймовірність появи того чи іншого результату експерименту.

Визначимо умовну ймовірність появи результату S_t експерименту в умовах стану природи П_j через

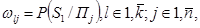(8.59)

Де символом Р позначена ймовірність.

Оскільки результати S₁,S₂, …,S_k експерименту утворюють повну систему подій, справедливо рівняння:

для 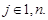(8.60)

В задачі припускається, що матриця W=|w_lj| розміру k*n умовних ймовірностей результатів експерименту повністю відома досліднику.

Повний об’єм початкової інформації в ЗПР, що розглядається в наступних даних:

1) множина можливих стратегій статистика Х={ х₁, х₂,..., х_м} і множина можливих станів „природи” П={ П₁, П_2, ..., П _п };

2) матриця розміру m*n виграшів статистика А=|a_ij|;

3) n – розмірний вектор апріорних ймовірностей стану природи Q=(q_j);

4) множина S={ S₁,S₂, …,S_k } можливих результатів одиничного експерименту;

5) матриця розміру k*n умовних ймовірностей результатів експерименту W=|w_lj|;

6) вартість С проведення експерименту (вимірюється в тих же одиницях, що й виграш статистика).

В описаній ситуації виникає два питання: 1) чи доцільно (із міркувань зростання виграшу статистика) проведення експерименту? 2) якщо проведення експерименту доцільне, то яка із стратегій повинна бути вибрана в якості оптимальної у випадку того чи іншого результату експерименту? Відповіді на ці питання представляють собою рішення ЗПР з одиничним неідеальним експериментом

Звернемось до розгляду послідовностей міркувань, що ведуть до рішення поставленої задачі. Представимо, що після реалізації експерименту з’явився результат S_t. Знаючи, що ми можемо уточнити ймовірності 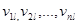станів природи П₁, П_2, ..., П _п при умові, що експеримент дав результат S_l. Шукані апостеріорні ймовірності можна підрахувати за відомою в теорії ймовірностей формулою Байеса:

для 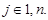(8.61)

Після того, як будуть визначені уточнення в результаті експерименту (апостеріорні) ймовірності 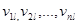станів природи П₁, П_2, ..., П _п, для кожної стратегії х_і, можна визначити середній виграш по формулі математичного сподівання:

(8.62)

Величина a_ij^сер має вигляд умовно середнього виграшу статистика від стратегії х_і при умові, що експеримент дав результат S_t.

Підрахувавши середні умовні виграші a_ij^сер для всіх стратегій статистика х₁, х₂,..., х_м можна визначити оптимальну стратегію х_tl, яка максимізує значення умовного середнього виграшу a_ij^сер. Стратегія х_tl є умовно оптимальною, тобто оптимальною при умові, експеримент дав результат S_t. Для позначення умовно-оптимальної стратегії використано два індекси: перший індекс t вказує номер оптимальної стратегії з множини можливих стратегій х₁, х₂,..., х_м, а в другій індекс l вказує при якому результаті з множини результатів S₁,S₂, …,S_k ця стратегія оптимальна.

Номер t умовно – оптимальної стратегії х_tl знаходиться з умови:

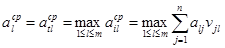(8.63)

Де a_i^сер – умовно-максимальний середній виграш (при умові, що експеримент дав результат S_t).

Описані розрахунки по формулах (8,61,(8,62),(8,63) відносяться тільки до одного результату експерименту - результату S_t. Вони дозволяють визначити умовно – опитимальну стратегію х_tl і відповідно їй умовно-максимальний середній виграш a_ij^сер в припущенні, що експеримент мав результат S_t.

Враховуючи, що проведення експерименту пов’язано з затратами засобів в кількості С, статистик повинен провести відповідні розрахунки раніше, до проведення експерименту і не для одного результату експерименту, а для всіх можливих результатів S₁,S₂, …,S_k, оскільки результати експерименту випадкові. В результаті цих розрахунків повинні бути визначені умовно – максимальні середні виграші a_i^сер і відповідні їм умовно – оптимальні стратегії х_tj для всіх можливих результатів експерименту.

Умовно – максимальний середній виграш a_i^сер є випадковою величиною. Ймовірність появи його різних значень співпадає з ймовірностями появи результатів експерименту S₁,S₂, …,S_k. Визначимо ймовірність появи результату S₁ h_t. Вона може бути визначена за формулою повної ймовірності, якщо відомі умовна ймовірність w_lj появи результату S_k при стані природи П_j та апріорна ймовірність q_j стану природи П_j:

(8.64)

Визначимо через a_екс^сер середнє значення максимального виграшу, яке може бути отримано при умові проведення експерименту. Велична цього виграшу може бути отримана по формулі математичного сподівання:

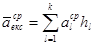(8.65)

Щоб вирішити питання про доцільність про проведення експерименту, необхідно порівняти виграш a_екс^сер з тим максимальним середнім виграшем, який може бути отриманий без проведення експерименту. Як було показано вище, величина a^сер визначається за формулою:

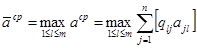(8.66)

Очевидно, що проведення експерименту можна вважати доцільним, якщо збільшення середнього виграшу за рахунок його проведення перевищує вартість експерименту. Іншими словами, проведення експерименту доцільне якщо виконується умова:

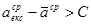(8.67)

Після того, як питання про питання доцільності проведення експерименту вирішено позитивно, дослідник повинен сформулювати для керівника операції правило, що визначає

яку стратегію 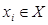необхідно прийняти при кожному з можливих результатів 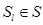експерименту. Це правило в теорії статистичних рішень називають вирішальним правилом. Визначимо визначальне правило символом d. Вирішальне правило d також називають вирішальною функцією і позначають у вигляді d(S_l)=x_i.

Пояснимо поняття вирішального правила на прикладі. Уявимо, що в деякій задачі простір стратегій складається з трьох елементів. Х={x₁,x₂,x₃}, а простір результатів експерименту – з п’яти елементів, тобто S={S₁, S₂, S₃, S₄, S₅}. Вирішальну функцію d(S_l)=x_i можна задати у вигляді множини пар індексів (l, i), що визначають номер стратегії x_i при результаті експерименту S_l. Вирішальною функцією може бути, наприклад, множина {(1,1),(2,1),(3.2),(4.2),(5.3)}. Це вирішальне правило означає. Що при результатах експерименту S₁та S₂ повинна бути прийнята стратегія х_l при результаті S₃ та S₄ – стратегія х₂, а при результаті S₅ – х₃. Звичайно приведена вирішальна функція не є єдиною можливою. Можна було б розглядати функцію {(1,1),(2,2),(3.2),(4.3),(5.3)} або функцію {(1,1),(2,1),(3.2),(4.2),(5.3)}. Сукупність всіх можливих вирішальних функцій створює простір D вирішальних функцій. Кожен ЗПР відповідає свій простір вирішальних функцій.

Поняття вирішальних функцій дозволяє більш чітко сформулювати задачу статистика. Ця задача полягає в тому, щоб з простору вирішальних функцій обрати вирішальну оптимальну функцію, що дозволяє приймати оптимальні рішення, тобто, вибирати при кожному результаті експерименту відповідну йому умовно – оптимальну стратегію.

Як вже відмічалось раніше, в теорії статистичних рішень немає одного принципу оптимальності. Одним з поширених принципів є баєовський принцип. Оптимальне баєсовське вирішальне правило ставить у відповідність кожному можливому результату експерименту S_t умовно – оптимальну стратегію х_tl, яка максимізує умовний середній виграш a₁^сер.

Проілюструємо описану процедуру рішення ЗПР в умовних природних невизначеностях з одиничним неідеальним експериментом на числовому прикладі.

Приклад.

Нехай розглядається гра з природною 3*4 умови якої приведені в таблиці 8.21. В нижньому рядку цієї таблиці представлені апріорні ймовірності Q=(q_j) можливих станів природи.

З метою уточнення обстановки проведення операції можливо проведення одиничного неідеального експерименту. Він може мати три можливих результати S₁, S₂, S₃. Умовні ймовірності цих результатів приведені в табл. 8.22.

Необхідно визначити при яких витратах на експеримент його проведення доцільне, а також визначити оптимальне баєсовське вирішальне правило.

Розв’язок.

Першочергово потрібно визначити максимальний середній виграш a^сер і оптимальну стратегію х_t для задачі без експерименту. Результати відповідних розрахунків приведено в табл. 8.23. Оптимальної баєсовської стратегії без проведення експерименту є стратегія х_t, а відповідний максимальний середній виграш a^сер=5,2.

Тепер перейдемо до визначення умовно – максимальних середніх виграшів a^сер і умовно – оптимальних стратегій х_l1, для кожного результату експерименту.

Результат S₁. Визначимо апостеріорні ймовірності v_ji станів природи при умові результату експерименту S₁.

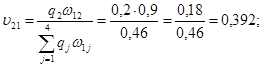
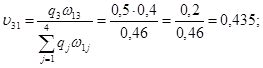
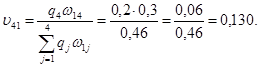
Перевірка:

З врахуванням апостеріорних ймовірностей v_ji табл. 8.21 перетворюється в табл. 8.24.

Таблиця 8.21 Таблиця 8.21

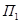
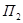
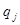
	0,1	0,2	0,5	0,2

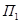
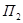
	0,2	0,9	0,4	0,3
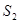
	0,1	0,1	0,5	0,3
	0,7		0,1	0,4

Таблиця 8.23 Таблиця 8.24

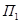
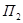
					5,2
					3,06
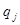
	0,1	0,2	0,5

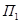
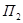
					4,96
					5,20
					5,09
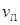
	0,043	0,392	0,435	0,130

При результаті експерименту S₁ умовно – оптимальних стратегій x_ti є стратегія х₂, а відповідний їй умовно – максимальний середній виграш a^сер=5,2.

Аналогічні розрахунки повинні бути проведені для результатів експерименту S₂ та S₃. Результати цих розрахунків представлені в табл. 8.25 та 8.26.

Таблиця 8.23 Таблиця 8.24

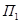
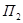
					5,53
					4,03
					5,23
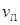
	0,029	0,059	0,735	0,177

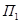
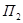
					5,20
					3,25
					3,7
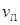
	0,35		0,25	0,4

При результаті експерименту S₂ умовно – оптимальної стратегії x_t2 є стратегія x₁, а відповідний їй умовно – максимальний середній виграш a₂^сер=5,53.

При результаті експерименту S₃ умовно – оптимальної стратегії x_t2 є стратегія x₁, а відповідний їй умовно – максимальний середній виграш a₃^сер=5,2.

Результати досліджень показують, що в даній задачі оптимальним баєсовським вирішуючим правилом є правило вигляду {(1.2),(2.1),(3.1)}, або інакше:

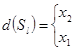
Словесне формулювання цього провила може бути такою: якщо експеримент дав результат S₁, застосовують стратегію x₂, в інших випадках – x₁.

Тепер відповісти на це питання потрібно визначити повний максимальний середній виграш, для чого, в свою чергу, потрібно визначити ймовірності h₁, h₂, h₃ результатів експерименту S₁, S₂, S₃.

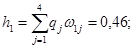
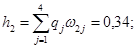
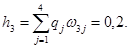
Перевірка:

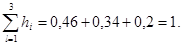
Максимальний середній виграш дорівнює

З порівняння максимальних середніх виграшів з експериментом і без експерименту виходить, що в задачі яку ми розглянули проведення експерименту доцільне, якщо пов’язані з ним затрати С задовольняють умові:

Чіі витрати 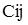на перевезення одиниці продукту з пункту Я до пункту j. Припускаємо що сумарний запас дорівнює сумарному попиту і для всіх 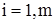i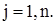

Потрібно скласти план перевезення продукту /або закріплення постачальників за споживачами/, коли запаси кожного постачальника було б вивезено, попит кожного споживача задоволено і загальні транспортні витрати мінімальні. Умови траспортної задачі звичайно записують у таблицях /табл. 8.4/.

Я	j			…	n	AЯ
	C11	C12	…	C1n	A1
	C21	C22	…	C2n	A2
…	…	…	…	…	…
m	Cm1	Cm2	…	Cmn	Am
Bj	B1	B2	…	Bn

Складаемо математичну модель задачі. Позначимо 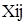шуканий план перевезення від постачальника Я до споживача j і розглядатимемо змінні 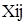, що задають цей план, як компоненти матриці перевезень Х розмірністю m*n:

/8.10/

Затрати пов’язані з деякими перевезеннями 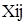, становитимуть величину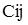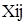, а загальна вартість перевезень Z від усіх постачальників до всіх споживачів

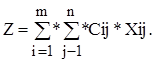/8.11/

згідно з постановкою задачі план перевезень треба скласти так, щоб вивезення від кожного постачальника дорівнюватиме обсягу виробництва:

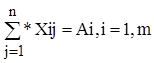/8.12/

а загаліні поставки будь-якому споживачеві задовольняли його попит:

/8.13/

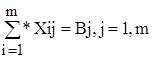
з фізичного змісту зміних випливають умови їх невід”ємності:

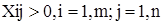/8.14/

Остаточно дістаємо таке формулювання транспортної задачі: знайти значення зміних 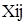,, які задовольняють умови /8.12/-/8.14/ і мінімізують функцію мети /8.11/.

Це кононічна задача лінійного програмування. У ній кількість зміних становить mn, a кількість обмежень-рівностей m+n. Ліві частини рівнянь /8.12/ утворюють рядкові, а /8.12/ та /8.13/ суми елементів Я-го рядка матриці Х і j-го стовпця мають дорівнювати відповідно AЯ і Bj. Тому рівняння /8.12 називають рядковим, а /8.13/- стовпцевим.

Вимогу запасу між сумарними запасами і потребами опусує умова сумісності

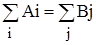\8.15\

системи обмежень /8.12/і /8.13/.

транспортну задачу для якої виконується умова балансу /9.15/,називають закритою. Коли цю умову пропущено,то кажуть що задача відкрита. Тут можливі два випадки:

сумарні запаси перевищують сумарний попит, коли, задовольнивши попит усіх споживачів, деякі постачальники мають не вивезений продукт.

Сумарний попит більший за сумарні запаси, тобто деяким споживачам буде завезено продукту менше, ніж вони потребують.

Відкриту модель легко перетворити на еквівалентну їй закриту.

Розв’язання транспортної задачі симплекс методом, як і кожної задачі лінійного програмування, складає ця з двох етапів: на першому деякий початковий опорний план, а на другому послідовно його поліпшують. Різновидом модифікованого симплекс-методу, пристосованого до особливостей транспортної задачі, є метод потенціалів, в якому опорні плани будуть елементарним способом, наприклад методом північно західного кута. Так називають процедуру побудови припустимого плану яку розпочинають з лівої верхньої клітинки таблиці, що описує умови транспортної задачі, і щоразу після вилучення стовпця (рядка) в під матриці,що залишаються, знову беруть ліве верхню клітинку.

Розглянемо приклад розв’язання транспортної задачі методом потенціалів.

Приклад 8.3 у місцях складування А1, А2, А3 (пунктах відправлення – ПБ) трьох дільниць цеху проміжного складання скупчується протягом години відповідно 30, 48, і 20 складених одиниць однієї назви

Для безперервного складання виробів потрібно, щоб періодично на стенди В1, В2, В3, В4,(пункти призначення -ПП) згідно з замовленнями надходили для комплектації 18, 27, 42, 11 складальних одиниць.

Вантажі можна перевозити з будь якого пункту А1, А2, А3, у будь який пункт В1, В2, В3, В4. відомі вартості 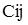перевезень одиниці вантажу з пункту Аі в пункт Вj. Вартості задано матрицею

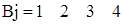
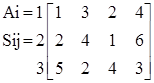
Сума запасів вантажу дорівнює сумі замовлень, тобто виконується умова сумісності /8.15/: 30+48+20=18+27+42+11=98. транспортну задачу можна зобразити табл.8.5 записавши її умови і вартості перевезень .

Транспортна задача - це задача на графі, що забезпечує мінімальну вартість перевезень чи доставляння вантажів до споживачів у найкоротший термін.

Теоретичне обґрунтування і способи розв’язання транспортної задачі на графовій моделі за критерієм вартості або за критерієм часу методами транспортних мереж та лінійного програмування викладено в

Таблиця 8.5

ПН   ПО	В1	В2	В3	В4	Запаси	Потенціал
А1				-1
А2
А3
Замовлення
Потенціал v				-1

Розв’яжемо транспортну задачу методом потенціалів.

Складемо допустимий план перевезень методом “північно-західного кута”. Заповнити таблицю 8.5 розпочнемо з лівого верхнього /”північно-західного”/ кута, тобто з клітинки А1-В1. До наступної клітинки рухатимемося праворуч або в них. Вартості перевезень поки що не беремо до уваги. Пункт В1 подав замовлення на 18 одиниць вантажу, яке можна задовольнити за рахунок запасів ПВ А1, тому в клітинку А1-В1 впишемо число 18. наступною клітинкою буде А1-В2, куди треба вмістити 27 одиниць вантажу. З А1 розташовуємо 12 одиниць. У клітинку А2-В2 з А2 випускаємо 15 одиниць, в А2-В3 з А3 9 одиниць в А3-В4 з А3 11 одиниць.

План називають допустимий коли всі замовлення виконано й усі запаси вичерпано.

Клітинки таблиці, перевезення в яких не дорівнюють нулеві, називають базисним. Допустимий план називають опорним, коли в ньому не

План перевезень називають оптимальними, коли він з-поміж усіх доступних планівдає мінімальну сумарну вартість перевезень.

План не оптимальний, бо під час його складання не враховано вартостей перевезень. Сумарна вартість за складеним планом

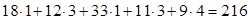
Для оптимізації плану перевезень запровадимо такі поняття й теореми.

1. Потенціалами опорного розв′язку називають такі числа та хдля всіх базесних клітинок.

Зауваження 1. Невідомих чисел та 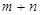, в кількість співвідношень для них становить 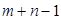, тому одне з цих чисел можна вибрати довільно. Припустимо, що . тоді решту невідомих можна визначити однозначно.

Зауваження 2. Суму потенціалів 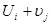називають псевдовартістю.

2. Якщо для всіх незаповнених клітинок то одержаний план оптимальний.

Розв′язання методом потенціалів складається з кількох етапів.

Перший етап. Визначимо потенціали, припустивши, що

Для клітинки , .

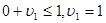Для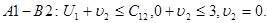

Для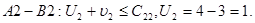

Для

Клітинка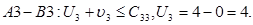

Клітинка .

Значення потенціалів занесемо в табл. 8.5

Другий етап. Підрахуємо псевдовартості для всіх вільних клітинок і їх значення впишемо в верхні кути вільних клітинок.

Псевдовартості /сума потенціалів/ відповідно дорівнббть для клітинок: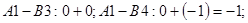

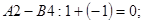
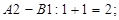
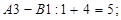
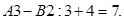
Чи оптимальний одержаний в таблиці план перевезень? Умова оптимальності_, У плані в клітинці 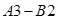псевдовартість дорівнює 7, а вартість 2. Оскільки 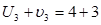>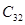, то побудовано неоптимальний план.

Третій етап. Побудуємо новий опорний план. Розглянемо цикл так званих перекидань. Одну з вершин циклу вмістимо у відділену клітинку 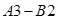, а решту – в базисні клітинки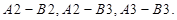

Такий цикл єдиний. Клітинкам надаємо почережні знаки «+» та «-». У виділеній клітинці 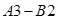табл. 8.5 ставимо знак «+».

Перемістимо по побудованому циклу найбільшу величину вантажу так, щоб новий план лишався опорним. У клітинках, це стоїть знак «+», вантаж додаємо, а»-» - зменшуємо /на одну й ту саму величину/. Яке число потрібно перемістити по виділеному циклу? Відповідь: 9 одиниць вантажу. Будуємо нову табл. 8.6. підрахуємо вартість перевезень за новим планом:

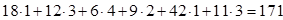
Звертаємо увагу на те, що вартість зменшилась на 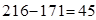цю величину можна дістати й іншим способом: де 7 – псевдовартість клітинки, 2 – її вартість, 9 – число, що його ми переміщували по циклу.

Таблиця 8.6

ПП ПВ	ВІ	В2	В3	В4	Запаси	Потенціал
АІ	І8
А2
А3			-1 4			-1
Замовлення
Потенціал

Щоб перевірити оптимальність нового плану, доведеться знову повернутися до першого етапу – підрахунку потенціалів.

Знайдемо значення потенціалів:

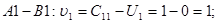
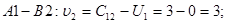
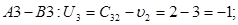
Знайдемо псевдо вартості 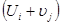для всіх вільних клітинок:

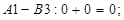
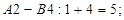
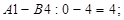
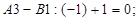
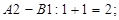
Перевіряємо за умовою 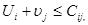чи є одержаний план оптимальним.Для клітинки 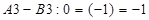< 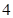і для решти псевцоклітинок умова виконується. Одержаний план – оптимальний, бо псевдо вартості не перевищують вартостей.

Отже, оптимальний план перевезень:

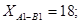
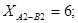
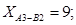
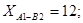
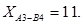
Загальна вартість усіх перевезень за цим планом становить 171.

План перевезень зображено на рис 8.2.

(30) (48) (20)

18 (1) 12 (3) 6 (4) 42 (1) 9 (2) 11 (3)

(18) (27) (42) (11)

Рис. 8.2. оптимальний план перевезень до прикладу 8.3.

Дата добавления: 2013-12-14