Случайная величина и её функция распределения вероятности

Для непрерывной случайной величины наиболее полной характеристикой является плотность функции распределения вероятности 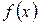, представленная на рис.2.2.

Величина 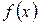пропорциональна вероятности того, что измеренная величина оказалась равной какому- либо конкретному значению. Например, вероятность того, что при измерении будет получено значение пропорциональна числу . Если формулировать математически точно, то нужно рассматривать интервал 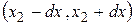. Вероятность того, что измеренная величина попадёт в указанный бесконечно малый интервал равна дифференциалу от плотности распределения вероятности

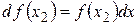, (4.1)

который геометрически равен площади заштрихованного участка в окрестности точки 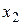. Равенство (2.1) справедливо для любой точки

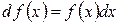, (4.2)

Будем обозначать вероятность какого либо события буквой Р, а само событие, выраженное математически, будем помещать в фигурные скобки. Тогда по определению плотности распределения вероятности, выполняется равенство

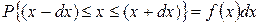, (4.3)

То есть, вероятность того, что измеренное значениепопадёт в интервал от до равна произведению плотности вероятности на величину этого интервала .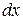

Наиболее вероятное значение соответствуем максимуму на кривой. Многочисленные исследования в самых различных областях науки и техники показывают: если измерения содержат случайную составляющую, которая возникает за счёт влияния большого количества факторов, причём каждый из них вносит малый вклад, то чем больше отклонение от наиболее вероятного значения, тем меньше вероятность такого отклонения. Поэтому, при смещении вправо и влево от , кривая носит убывающий характер. Кроме того, кривая симметрична относительно оси, проходящей через наиболее вероятное значение. Это означает, что отклонения от с завышением и с занижением равновероятны.

Если проинтегрировать функцию плотности распределения вероятности (см. рис.4.2), то получим интегральную функцию распределения вероятности ,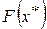

, (4.4)

В общем случае случайная величина может изменяться от 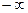до 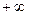, тогда нижним пределом в интеграле будет 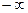.Интегральная функция распределения (или просто функция распределения) представлена на рис.4.3.

Поскольку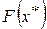является первообразной для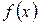, соотношение между этими функциями определяется основной теоремой интегрального исчисления (теоремой Ньютона − Лейбница)

. (4.5)

Из соотношения (4.4) следует статистический смысл функции распределения вероятности. Она показывает, какова вероятность того, что значение

измеряемой величины попадёт в конечный интервал 0 <<(или в интервал −∞ << )

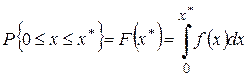. (4.6)

Если, например, требуется определить вероятность попадания измерения в интервал от 0 до , то эта вероятность равна (см. рис. 4.3), что соответствует заштрихованной площади криволинейной фигуры с основанием (0,) (см. рис.4.2). Но событие попадания измеряемой величины на относительно большой интервал (0,) означает логическую сумму событий попадание или на первый малый участок , или на второй малый участок , или на третий участок 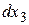и так далее. Каждому из этих событий соответствуют вероятности 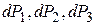и так далее. В этом случае вероятности складываются

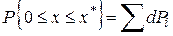. (4.7)

Поэтому функцию распределения вероятностей можно назвать функцией «накопленной» вероятности.

Рассмотрим некоторые естественные свойства рассмотренных функций, вытекающие из их определения:

1.Поскольку попадание положительно определённой случайной величины в интервал от 0 до бесконечности обязательно произойдёт, то есть является достоверным событием, а вероятность достоверного события равна 1, выполняется равенство (условие нормировки)

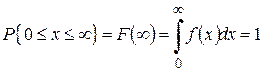. (4.8)

2.Вероятность попадания на больший интервал (0,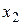) больше, чем на меньший (0,), поэтому функция распределения вероятности является возрастающей

. (4.9)

3.Из определения функции 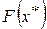вытекают равенства при

,

,

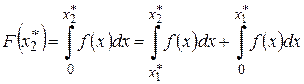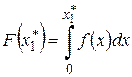Откуда следует, что вероятность попадания случайной величины в интервал определяется выражением

, (4.10)

что геометрически соответствует

Дата добавления: 2013-12-13