Системи координат, що застосовуються у вищій геодезії

Рис. 1.1

Отже, існують в основному три (рис.1.1) різні можливі поняття "фігура Землі":

а) фізична або дійсна Земля - тверда і рідка частини Землі. Вона є надзвичайно нерегулярною навіть після деякого згладження. Згладжена поверхня піддається математичному опису після деякого усереднення в часі (геодинамічні ефекти);

б) геоїд чи квазігеоїд;

в) земний еліпсоїд.

Приведемо ще декілька понять, що використовуються у вищій геодезії.

Еліпсоїд, що найбільш близько підходить до фігури Землі в цілому і центр якого збігається з центром мас Землі, називається загальним земним еліпсоїдом, а еліпсоїд, що найбільш близько підходить до поверхні геоїда на певній території (в межах держави, регіону чи континенту) і центр якого хоч і близько підходить, але не збігається з центром мас Землі називається референц-еліпсоїдом.

Отже, референц-еліпсоїд - це земний еліпсоїд, вісь якого паралельна осі загального земного еліпсоїда і який взятий для опрацювання геодезичних вимірів та встановлення системи геодезичних координат.

Системою координат називається сукупність умов, що визначають положення точки на прямій, площині, кривій поверхні, в просторі.

Системи координат, що застосовуються в сучасній геодезії, можна розділити на групи: прямолінійні (двовимірні - на площині, тривимірні - в просторі); сферичні (двовимірні - на сфері, тривимірні - в просторі), еліпсоїдальні (двовимірні - на поверхні еліпсоїда, тривимірні - в просторі) тощо.

Прямолінійні координати - двовимірні на площині - можуть бути полярними координатами на площині, а сферичні координати деколи називають полярними координатами в просторі. Вони можуть відрізнятися за формою, що задається, і бути: прямокутними і криволінійними. Але принципові відмінності систем координат обумовлюються вибором початку, основної координатної площини та головної осі координат.

Система координат, початок якої знаходиться в центрі мас Землі або близько нього, називається геоцентричною та квазігеоцентричною відповідно. Звідси, координати, пов'язані з загальноземним еліпсоїдом, будуть загальноземними і геоцентричними, а координати, пов'язані з вибраним референц-еліпсоїдом, - референцними і квазігеоцентричними. Якщо ж початок координат збігається з пунктом спостереження на земній поверхні (топоцентром), то систему координат називають топоцентричною.

В залежності від вибраної основної координатної площини розрізняють екваторіальну (екватор або площина, паралельна екватору), екліптичну (площина екліптики), горизонтну (площина місцевого горизонту) та орбітальну (площинаорбітинебесного об'єкта) системи координат.

В залежності від вибраного напряму осей координат відносно точок простору, системи координат поділяють на: зоряні, якщо вони зорієнтовані за далекими зорями (вивчаються в курсі “Геодезична астрономія”), квазарні, якщо вони зорієнтовані за далекими природніми радіоджерелами (квазарами); земні, якщо вони зорієнтовані за нерухомими точками на земній поверхні.

Напрями осей вибраної системи координат в просторі можуть бути задані відносно характерних точок небесної сфери або земної поверхні. У відповідності з цим слід розрізняти системи координат, що не обертаються і що обертаються разом з Землею.

В геодезії широке застосування мають особливі системи пов'язаних з Землею координат, основні координатні площини та головні осі яких збігаються відповідно з площиною земного екватора і віссю обертання Землі, або є паралельними до них. В од­ній із цих систем координат положення точки земної поверхні характеризується компонентами напряму прямовисної лінії в цій точці відносно координатних площин або нерухомих зірок. Оскільки положення точки земної поверхні в цій системі координат, що обертається разом з Землею, може бути визначене безпосередньо із астрономічних спостережень в цій точці, то ця система координат називається астрономічною.

Отже, астрономічні координати - компоненти напряму прямовисної лінії в даній точці простору відносно площини перпендикулярної до осі обертання Землі та площини початкового астрономічного меридіана.

Астрономічною широтою точки Q на поверхні Землі називається кут φ (рис. 1.2), утворений площиною екватора та напрямком прямовисної лінії в цій точці.

Астрономічною довготою точки Q на поверхні Землі називається двогранний кут λ, утворений площинами початкового (Грінвіцького) меридіана та астрономічного меридіана даної точки.

Площина астрономічного меридіана проходить через прямовисну лінію в даній точці паралельно осі обертання Землі.

Фігура Землі, як було сказано вище, в загальному має сфероїдний вид, тому для побудови системи координат вона замінюється деяким еліпсоїдом обертання з ві­домими розмірами та заданим положенням в тілі Землі. Положення точок земної по­верхні характеризується компонентами напрямів нормалей до поверхні прийнятого еліпсоїда в цих точках та їх висотами над поверхнею цього еліпсоїда. Оскільки згадувані характеристики положення точок в цій системі координат визначаються за результатами геодезичних спостережень, то сама система називається геодезичною.

Астрономічна і геодезична системи координат можуть бути задані у вигляді як поверхневих криволінійних координат, так і прямокутних прямолінійних.

При заданні геодезичних координат у виді поверхневих криволінійних, паралелі та меридіани приймають за систему ортогональних координатних ліній на еліпсоїді, а за координати приймають кутові величини. Перейдемо до їх розгляду.

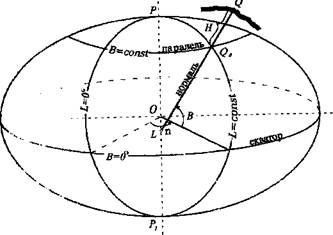
Приймемо один з меридіанів за початковий. Тоді положення будь-якого другого меридіана буде визначатися двогранним кутом, утвореним площинами початкового та даного меридіанів. Цей кут має одну і ту ж величину для всіх точок даного меридіана і, відповідно, може бути прийнятий за координату для меридіана. Він позначається буквою L (рис. 1.3)і називається геодезичною довготою.

Довготи, що відраховуються від площини початкового меридіана на схід (в полюсі проти руху годинникової стрілки) в межах від 0 до +180° називаються східними довготами, а на захід в межах від 0 до -180° - західними довготами.

Отже, меридіан є координатна лінія, у всіх точках якої геодезична довгота має одну і ту ж величину (L=const). Зазначимо, що площина геодезичного меридіана проходить через нормаль до поверхні еліпсоїда Q₀і вісь обертання еліпсоїда РОР ₁(рис. 1.3). Внаслідок симетричності поверхні еліпсоїда відносно меридіанапряма Q₀ n буде перпендикулярна одночасно до дотичної до меридіана і до дотичної допаралелі, відповідно вона перпендикулярна до дотичної площини в точціQ₀.

Дата добавления: 2013-12-14