Теорема о существовании и единственности решения задачи Коши для линейных систем ОДУ в нормальной форме

Лекция 13

Определение 1.

Пусть 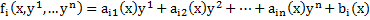при 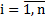. Тогда система 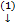называется линейной.

В этом случае 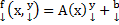, где:

A(x)=;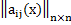

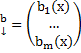
Т.е. уравнение 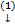примет вид:

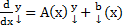
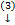
Теорема 3. Обобщение принципа сжимающих отображений.

Пусть X - полное метрическое пространство, в котором действует оператор A: Х Х, и пусть 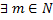: оператор 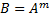- сжимающий. Тогда у A 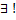неподвижная точка .

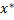Доказательство.

При m=1 утверждение верно, т.к. оно совпадает с утверждением теоремы 1, которую мы уже доказали.

Рассмотрим m>1.

Т.к. 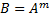– сжимающий оператор → по теореме 1 → 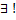неподвижная точка .

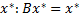Заметим, что оператор “A” и “B” коммутируют: 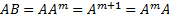=BA.

Также, заметим, что: 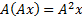- т.е. оператор, возведенный в степень – это повторение действия оператора “m” раз.

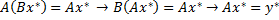→ - неподвижная точка для оператора В → по теореме 1 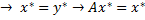, где 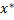- неподвижная точка для оператора А.

Докажем единственность точки .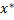

Пусть 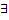точка .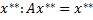

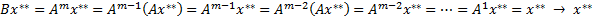- неподвижная точка для оператора В → по теореме 1 → .

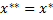Что и требовалось доказать!

Теорема 4. Т.С.Е. решение З.К. для линейных систем ОДУ в нормальной форме.

Пусть 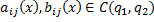(причем, может быть, что ).

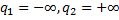Тогда для задача Коши 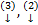имеет единственное решение 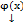, определенное при .

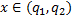Замечание.

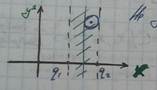Посмотрим, чем же эта теорема отличается от теоремы 2?

В теореме 2, область 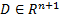- область определения .

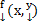А теперь посмотрим, чем является область D для теоремы 4, точнее, системы .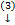

:

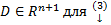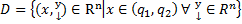
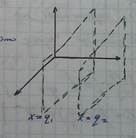Изобразим эту область (приблизительно).

На двумерной плоскости, это целая бесконечная полоса – объединения двумерных прямых.

Для трехмерной плоскости это целый слой – объединения двумерных плоскостей.

Что все это нам дает?

В теореме 2 мы жестко регулировали размеры «цилиндра», чтобы доказать теорему внутри него → теорема имеет локальный характер.

В теореме 4 мы можем взять срезу бесконечные размеры цилиндра → можем доказать больше → теорема имеет глобальный характер.

Доказательство.

Для .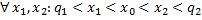

Рассмотрим сегмент 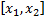и множество непрерывных вектор-функций на этом сегменте 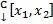(по сути, это цилиндр бесконечного радиуса). Пусть 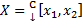- это метрическое пространство с метрикой

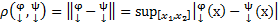
Множество X - это полное метрическое пространство. Тогда рассмотрим оператор А:

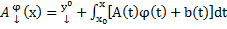- оператор в X.

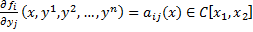
по теореме Вейерштрасса → ограничены на .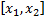

Обозначим через .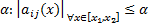

Тогда 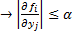при 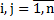. - ограничены в области .

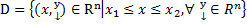С другой стороны, D - выпуклое множество → по лемме → 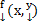удовлетворяет условия Липшица по 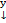при фиксированном x:

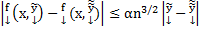
Оценим норму двух произвольных функций .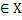

Пусть .

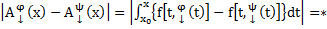→ по лемме 1 →

→ (*)

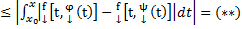
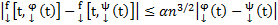
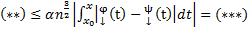
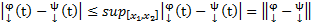
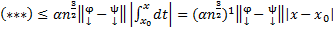,(m=1)

Рассмотрим m=2. Получим следующее:

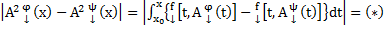
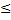(*)проводим аналогичные m=1 рассуждения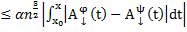

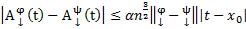
→ применяя неравенство с m=1 → 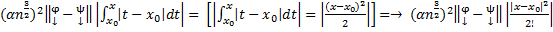, (это для m=2).

Проделав аналогичные действия для m=3,4…, сможем обобщить 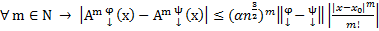для для .

Заметим, что .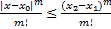

Отсюда:

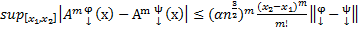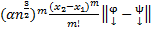, (- некое число = const)

Т.к.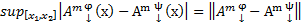

→

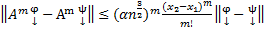
Обозначим через →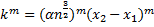

→

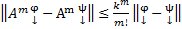
Заметим, что 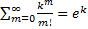→ 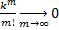- сходящийся ряд

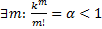→ → мы получили, что для

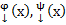
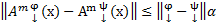, где , , →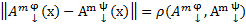

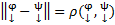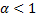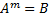→ - сжимающий оператор в множестве Х.

По теореме 3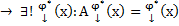

т.е. З.К. 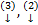на 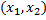имеет решение и оно единственно.

Мы получили, что:

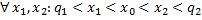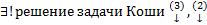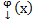, ,на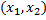

Построим 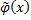при :

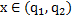для :

:

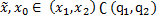По уже доказанному: 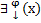! решение задачи Коши на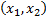

Положим

__________

И возникает вопрос, единственным ли образом мы определяем 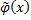? – да, т.к. если есть два решения → на их общей области определения они совпадают.

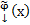- решение задачи Коши на .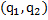

__________

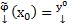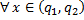Эта функция удовлетворяет начальным условиям , для и 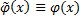в некоторой окрестности точки Х, где Х – некоторое решение задачи Коши, область определения которого содержит точку x и 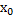. → 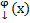удовлетворяет 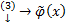удовлетворяет 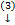в окрестности точки Х.

Что и требовалось доказать!

Дата добавления: 2013-12-13