Диаграмма разброса

Диаграмма разброса – один из инструментов контроля качества, позволяющий визуально определить вид и тесноту связи между двумя случайными величинами. Другое название диаграммы разброса – поле корреляции. В качестве случайных величин наиболее часто выступают:

1 Показатель качества и фактор производства;

2 Два показателя качества;

3 Два фактора производства.

Для построения диаграммы разброса данные собирают парами. На диаграмме разброса одной паре данных соответствует одна точка разброса. Считается, что точек должно быть не менее 25-30.

Рассмотрим случай, когда в качестве одной из случайных величин выступает показатель качества, другой – фактор производства.

Последовательность применения диаграммы разброса для этого случая будет состоять из следующих этапов:

1 Осознание неудовлетворенности качеством изделия в целом, его деталей и узлов или качеством технологического процесса.

2 Выбор показателя качества, количественно отражающего эту неудовлетворенность.

3 Выдвижение гипотезы о влиянии какого-либо фактора производства на выбранный показатель качества.

4 Сбор парных данных, т.е. значений показателей качества и факторов производства.

5 Построение диаграммы разброса и её анализ. В результате анализа диаграммы может быть сделан один из следующих выводов:

5.1 Связь присутствует и достаточно сильна: выбранный фактор производства сильно связан с показателем качества, выдвинутая гипотеза верна. В этом случае, изменяя фактор производства, можно добиться требуемого значения показателя производства и, тем самым, улучшить качество. Требуемое изменение фактора производства количественно можно оценить с использованием уравнения прямой выборочной регрессии.

5.2 Связь присутствует, но не достаточно сильная: выбранный фактор производства слабо связан с показателем качества. Изменяя данный фактор, можно до некоторой степени управлять показателем качества, однако необходимо продолжить поиск факторов, так же влияющих на этот показатель, выдвинув новые гипотезы. Следует, не исключая из рассмотрения текущего фактора производства, найти другие факторы, влияющие на показатель качества, выполнив п.3 - п.5 описываемой последовательности. Требуемое качество может быть достигнуто одновременным изменением всех выявленных влияющих факторов производства.

5.3 Связь не установлена: выбранный фактор производства не связан с показателем качества, гипотеза неверна. Продолжаем поиск факторов. Следует найти факторы производства, влияющие на показатель качества, исключив при поиске из рассмотрения текущий фактор. Новый поиск также проводится в соответствии с последовательностью п.3 - п.5.

Дополнительная информация:

· Следует отметить, что если две переменные кажутся связанными, это не означает, что они таковыми являются.

· Если данные не кажутся связанными, это не означает, что они не связаны: просто приведено недостаточно данных или данные следует разбить по классам и построить по каждому классу свою диаграмму, а возможно допущена большая ошибка при измерении и т. д.

Построение диаграммы разброса необходимо проводить в следующей последовательности:

1 Собрать парами значения (x ₁, y ₁), (x ₂, y ₂),... (x_n, y_n) случайных величин X и Y, между которыми требуется исследовать зависимость. Расположить их в таблицу. Желательно не менее 25-30 пар данных.

2 Найти максимальные и минимальные значения для X и Y. Выбрать шкалы на горизонтальной и вертикальной осях так, чтобы их длины были приблизительно одинаковыми. Если одна переменная – фактор производства, а вторая – показатель качества, то выбрать для фактора горизонтальную ось, а для показателя качества – вертикальную.

3 Нанести точки, соответствующие парам данным, на диаграмму.

4 Сделать все необходимые обозначения. Убедиться, что нижеперечисленные данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто делал диаграмму:

4.1 Название диаграммы.

4.2 Интервал времени, когда были получены данные.

4.3 Число пар данных.

4.4 Названия и единицы измерения для каждой оси.

4.5 Условия получения данных.

4.6 Имя человека, сделавшего диаграмму.

Типичные варианты скопления точек на диаграмме разброса приведены на рисунке 9.

Рисунок 9 – Типичные варианты скопления точек на диаграмме разброса

На графике (рис.1) рисунка 9 изображена сильная прямая корреляция. Величины X и Y связаны. Увеличивая X можно увеличить Y.

На графике (рис.2) рисунка 9 изображена легкая (слабая) прямая корреляция. Величины X и Y связаны, однако на величину Y кроме Х действую какие-либо другие величины. Увеличивая X также можно увеличить Y.

На графике (рис.3) рисунка 9 изображена сильная обратная корреляция. Величины X и Y связаны. Увеличивая X можно уменьшить Y.

На графике (рис.4) рисунка 9 изображена легкая (слабая) обратная корреляция. Величины X и Y связаны, однако на величину Y кроме Х действую какие-либо другие величины. Увеличивая X также можно уменьшить Y.

На графике (рис.5) рисунка 9 приведено скопление точек, характерное для отсутствия корреляции. Величины X и Y не связаны.

На графике (рис.6) рисунка 9 изображена криволинейная корреляция. Величины X и Y связаны, в отличие от случаев (рис.1) – (рис.4) нелинейной зависимостью.

Если при анализе диаграммы разброса установлена связь между случайными величинами X и Y, то, изменяя X, можно добиться требуемого значения Y (или наоборот). Если при этом выявленная связь может считаться линейной, то количественное изменение одной из случайных величин, необходимое для получения определенного значения другой, может быть найдено с помощью уравнения прямой выборочной регрессии.

Пусть в результате n испытаний получены пары значений случайных величин X и Y:

(x ₁, y ₁), (x ₂, y ₂),.....(x_n, y_n). (58)

Допустим, что случайная величина Y имеет вид

Y = Y ₀+ V, (59)

где Y ₀ – случайная величина, связанная с Х линейной функциональной зависимостью (формула 60),

V – случайная величина, отражающая влияние на Y неизвестных случайных факторов.

Y ₀= kX + b, (60)

где k и b – некоторые неизвестные постоянные.

Если бы V =0, то все точки поля корреляции, соответствующие парным данным, принадлежали бы прямой

y = kx + b. (61)

Данное уравнение является уравнением прямой выборочной регрессии.

Таким образом, одна из задач корреляционного анализа заключается в отыскании по опытным данным коэффициентов линейной зависимости (60).

Пусть величина

(62)

выражает степень удаленности точки i от прямой (61). Чем меньше разности в совокупности, тем «ближе» проходит прямая (61) от множества точек (58), тем лучше она отражает искомую зависимость. Пусть «расстояние» от прямой до системы точек выражается равенством:

. (63)

Наилучшей прямой, т.е. прямой с меньшим «расстоянием» от совокупности точек (58), будет являться такая прямая, которая соответствует минимуму функции R (k, b).

Минимум функции R (k, b) достигается в точке с координатами:

, (64)

. (65)

Прямая (61), для которой сумма квадратов (63) достигает наименьшего значения, называется прямой выборочной регрессии. Если чертой сверху обозначить среднее значение соответствующей величины, то выражения (64, 65) можно записать в виде:

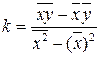, (66)

. (67)

Число 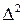, равное значению функции R (k, b), где k и b определены из равенств (64, 65) называется остаточной дисперсией.

Для определения тесноты связи случайных величин используют коэффициент корреляции

. (68)

Коэффициент корреляции обладает следующими свойствами:

1) r =0 если величины X и Y не связаны.

2) | r |=1 если величины X и Y связаны зависимостью вида (61).

Необходимо заметить, что коэффициент корреляции (68) корректно отражает тесноту связи случайных величин, если зависимость между ними линейная.

Дата добавления: 2013-12-13