Интерполяция и экстраполяция

Аппроксимация

Аппроксимация, или приближение, — замена одних математических объектов другими, в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимациикривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например теория приближения функций, численные методы анализа.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции g(x) (аппроксимирующей функции), котораябыла бы близка заданной. Критерии близости функций f(x) и g(x) могут быть различные. В том случае, когда приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной. В том случае, когда аппроксимация проводится на непрерывном множестве точек (отрезке), то аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, т. е. замена некоторой функции степенным многочленом. Например:

• для приближенного вычисления интеграла используется формула прямоугольников или формула трапеций, или бо­лее сложная квадратурная формула. Фактически при этом происходит приближение подынтегральной функции сту­пенчатой функцией или вписанной ломаной;

• для вычисления значений сложных функций часто исполь­зуется вычисление значения отрезка ряда, аппроксимирую­щего функцию.

Интерполяция — способ нахождения промежуточных значе­ний величины по имеющемуся дискретному набору известных значений.

В научных и инженерных расчетах часто приходится опери­ровать наборами значений, полученных экспериментальным пу­тем или методом случайной выборки. Как правило, на основа­нии этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые зна­чения. Например, известны некоторые значения функции — физической величины, замеренные через 1 ч. Необходимо найти значения в промежутках через 30 мин.

Интерполяцией называют такую разновидность аппроксима­ции, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Существует также близкая к интерполяции задача, которая включается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно по­пытаться вычислить ее значение в нескольких точках, а по ним построить, т. е. интерполировать, более простую функцию. Разу­меется, использование упрощенной функции не позволяет полу­чить такие же точные результаты, какие давала бы первоначаль­ная функция, но в некоторых классах задач достигнутый выиг­рыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.

Большая часть классического численного анализа основывается на приближении многочленами, так как с ними легко работать. Однако для многих целей используются и другие классы функций.

Выбрав узловые точки и класс приближающих функций, мы должны ещё выбрать одну определённую функцию из этого класса посредством некоторого критерия — некоторой меры приближения или «согласия». Прежде чем начать вычисления, мы должны решить также, какую точность мы хотим иметь в ответе и какой критерий мы изберём для измерения этой точности.

Всё изложенное можно сформулировать в виде четырёх вопросов:

1. Какие узлы мы будем использовать?

2. Какой класс приближающих функций мы будем использовать?

3. Какой критерий согласия мы применим?

4. Какую точность мы хотим?

Существуют 3 класса или группы функций, широко применяемых в численном анализе. Первая группа включает в себя линейные комбинации функций 1, х, х2, …, хn, что совпадает с классом всех многочленов степени n (или меньше). Второй класс образуют функции cos(x), sin(x). Этот класс имеет отношение к рядам Фурье и интегралу Фурье. Третья группа образуется функциями e-az. Эти функции встречаются в реальных ситуациях. К ним, например, приводят задачи накопления и распада.

Что касается критерия согласия, то классическим критерием согласия является «точное совпадение в узловых точках». Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за игнорирования шума (погрешности, возникающей при измерении или вычислении значений в узловых точках). Другой относительно хороший критерий — это «наименьшие квадраты». Он означает, что сумма квадратов отклонений в узловых точках должна быть наименьшей возможной или, другими словами, минимизирована. Этот критерий использует ошибочную информацию, чтобы получить некоторое сглаживание шума. Третий критерий связывается с именем Чебышева. Основная идея его состоит в том, чтобы уменьшить максимальное отклонение до минимума. Очевидно, возможны и другие критерии.

Более конкретно ответить на поставленные 4 вопроса можно лишь исходя из условий и цели каждой отдельной задачи.

Интерполяция многочленами

Цель задачи о приближении (интерполяции): данную функцию у(х) требуется приблизительно заменить некоторой функцией j(х), свойства которой нам известны так, чтобы отклонение в заданной области было наименьшим. интерполяционные формулы применяются, прежде всего, при замене графически заданной функции аналитической, а также для интерполяции в таблицах.

Наиболее часто встречающимся видом точечной аппрокси­мации является интерполяция. Пусть задан дискретный набор то­чек х_i, (i =0, 1,..., п), называемых узлами интерполяции, причем среди этих точек нет совпадающих, а также значения функции y_i в этих точках. Требуется построить функцию g(x), проходящую через все заданные узлы. Таким образом, критерием близости функции является g(x_i) = y_i. В качестве функции g(x) обычно выбирается полином, который называют интерполяционным по­линомом. В том случае, если полином един для всей области ин­терполяции, говорят, что интерполяция глобальная.

В тех случаях, когда между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции. Найдя интерполяционный полином, можно вычислить значения функ­ции f(x) между узлами (провести интерполяцию в узком смысле слова), а также определить значение функции f{x) даже за пре­делами заданного интервала (провести экстраполяцию).

Пусть имеется п значений х_i,каждому из которых соответст­вует свое значение у _i. Требуется найти такую функцию F, что:

F(x_i) =y_i, i = 0, 1,..., п. (1).

При этом:

• х_i называют узлами интерполяции;

• пары (х _{i ,} у_i) называют точками данных;

• разницу между соседними значениями (х _i -х _i-1) называют шагом;

• функцию F(x) — интерполирующей функцией или интерполянтом.

Задача интерполирования состоит в том, чтобы по значени­ям функции в некоторых точках восстановить ее значения в ос­тальных точках отрезка. Функция F называется интерполирую­щей, точки х₀, х₁, х₂,..., х_n — узлами интерполяции.

Будем искать функцию F в виде многочлена степени п:

F(x) = a_0·xⁿ + a_n-1·x^{n -1… +}a_n-1·x + a_{n. (2).}

Можно найти коэффициенты а_i, i = 0, 1,..., п, при этом полу­чим систему из (п + 1) уравнения с
(п +1) неизвестными

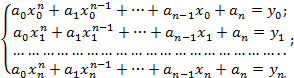(3).

Эта система имеет единственное решение, так как по наше­му предположению все х _i различны. Решая эту систему относи­тельно неизвестных а₀, а₁,..., а_п, получим аналитическое выра­жение многочлена.

Описанный прием можно использовать при решении задач интерполирования, но на практике используют другие более удобные и менее трудоемкие методы.

Дата добавления: 2013-12-13