Методы интегрирования в определенном интеграле

Задача (3) о глубине проникновения воды в почву (о площади криволинейной трапеции).

Задача (2) о работе переменной силы.

Задача (1) о количестве вещества, вступившего в реакцию.

План лекции.

Лекция. Определенный интеграл, его свойства и приложения.

(4 часа)

1. Задачи, приводящие к определению определенного интеграла.

2. Понятие определенного интеграла.

3. Свойства определенного интеграла, формула Ньютона-Лейбница.

4. Методы интегрирования в определенном интеграле (замена переменной и интегрирование по частям).

5. Приложения определенного интеграла.

· Геометрические приложения (площадь плоской фигуры; длина дуги; площадь поверхности вращения; объем тела).

· Физические приложения (работа силы; масса; статические моменты, координаты центра тяжести).

· Биологические и экологические приложения (численность популяции, биомасса популяции, средняя длина пролета птиц).

6. Приближенное вычисление определенных интегралов (формула прямоугольников, формула трапеций, метод Симпсона).

1.Задачи, приводящие к понятию определённого интеграла.

Вычислим глубину проникновения воды в почву при условии, что скорость инфильтрации задана функцией 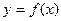, где 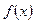– скорость инфильтрации в мм/час, а – время в часах за отрезок времени от 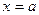до .

(рис. 2.)

Общее количество воды, просочившейся в почву за некоторый промежуток времени, графически представляется площадью, расположенной под кривой между границами временного интервала на оси .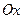

Мы столкнулись с задачей определения площади криволинейной трапеции.

Мы можем рассматривать площадь прямоугольника как самое грубое приближение к площади криволинейной трапеции. Можно улучшить наше приближение, взяв, сумму более мелких прямоугольников.

Разобьём отрезок точками

на n частей,

положим . Наибольшую из этих разностей обозначим через λ: .

(рис. 3)

На каждом отрезке [x_k-1, x_k], 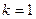, n выберем произвольную точку. Тогда – даёт площадь прямоугольника с основанием 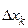и высотой .

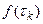Тогда сумма – даёт приблизительно площадь криволинейной трапеции.

Если 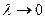, то эта сумма будет стремиться к точному значению площади трапеции, то есть

(*)

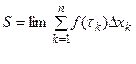2. Понятие определённого интеграла.

О Если существует предел (*), не зависящий от способа разбиения отрезка [а,b] и выбора точек ò _k, то этот предел будем называть определённым интегралом функции f(x) на отрезке [а; b] и обозначать

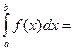
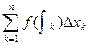
f(x) – подынтегральная функция

f(x)dx – подынтегральное выражение

а – нижний предел интегрирования

b – верхний предел интегрирования

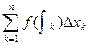_- интегральная сумма

3. Свойства определённого интеграла. Формула – Лейбница.

1⁰ 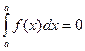– определённый интеграл с равными верхним и нижним пределами равен нулю.

2⁰ – постоянный множитель можно выносить за знак определённого интеграла.

3⁰ – определённый интеграл от

суммы двух функций равен сумме определённых интегралов от этих функций.

4⁰ – при перестановке пределов интегрирования

определённый интеграл меняет свой знак.

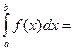
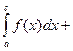
5⁰ , где a < c < b – интеграл по отрезка равен

сумме интегралов по его частям.

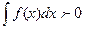6⁰ Если функцияна отрезке [а,b], то – это свойство

следует из геометрического смысла определённого интеграла.

7⁰ Формула Ньютона – Лейбница. Если функция f(x) непрерывна на сегменте [а,b] и F(x) – первообразная функции f(x) на этом отрезке, то

Эта формула называется формулой Ньютона – Лейбница, она даёт удобное правило вычисления определённого интеграла. Кроме того, она устанавливает связь между определённым и неопределённым интегралами.

Пример: Вычислить глубину проникновения воды в почву, если скорость инфильтрации задана формулой (мм/час) за время от x = 0,01ч до x = 0,25 часа.

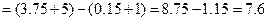(мм)

4.1. Замена переменной в определённом интеграле.

Предположим, что функция f(x) непрерывна на сегменте [а,b], функция 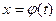имеет на сегменте [α, β] непрерывную производную, при этом 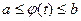и 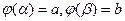. Пусть F(x) – одна из первообразных функции f(x). Тогда 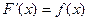и в силу формулы производной сложной функции:

Теперь воспользуемся дважды формулой Ньютона – Лейбница:

.

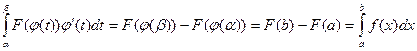Таким образом, - формула замены переменной в определённом интеграле.

Пример:

Замечание: В отличие от неопределённого интеграла в определённом при замене переменной к старой переменной не возвращаемся.

Дата добавления: 2013-12-13