Системы ортогональных многочленов

Имея в виду, что нас интересует, в первую очередь, полиномиальная аппроксимация функций, и при этом известны недостатки степенных функций для их использования в качестве базисных при построении многочленов наилучших среднеквадратических приближений и отмечены достоинства ортогональных многочленов в этой роли (§19.1), приведем некоторые сведения справочного характера о последних.

Многочлены Лежандра P_n (x) – наиболее употребительные из классических ортогональных многочленов и единственные, для которых условие их ортогональности на отрезке [–1, 1] выполняется «в чистом виде», т.е.

Известна формула Родрига

(19.7)

которая дает возможность в явном виде представить многочлены Лежандра.

Положив P ₀ =1 и найдя по формуле (19.7) P ₁ =х, все последующие многочлены Лежандра можно получать один за другим с помощью рекуррентной формулы

При п = 1, 2, 3,... из нее имеем соответственно:

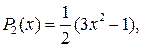
и т.д. 8

Сравнивая многочлены Лежандра с рассмотренными в §18.1 многочленами Чебышева, можно обнаружить, что их сходство — не только внешнее. Эти многочлены характеризует ряд одинаковых свойств. Например, как и многочлены Чебышева, многочлены Лежандра n -й степени имеют на отрезке [-1, 1] ровно п различных действительных корней (см. свойство 18.1). В то же время, как и многочлены Лежандра, многочлены Чебышева Т_n (х) относятся к числу классических ортогональных многочленов, но ортогональность здесь понимается в более широком смысле — это ортогональность с весом. А именно, условие ортогональности многочленов Чебышева Т_n (х) на отрезке [-1, 1] имеет вид

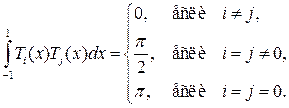
Многочлены Лагерра L_n (x) определяются требованием их ортогональности на промежутке [0, +¥) с весовой функцией е^–x, а именно условием

Как и предыдущие ортогональные многочлены, многочлены Лагерра удовлетворяют рекуррентному соотношению

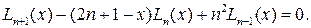
Так как L ₀ = 1, L ₁= - х + 1. Отсюда легко получить несколько первых многочленов Лагерра:

L ₂(x) =x ²-4 x + 2,

L ₃(x) = - x ³+9 x ² - 18 x +6,

L₄ = х ⁴ -16 x ³+72 x ² - 96 x +24.

Многочлены Эрмита Н_n (х) ортогональны на всей числовой оси с весом 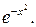Они удовлетворяют интегральному условию ортогональности

и рекуррентному соотношению

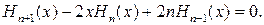
Так как H ₀ = 1, H ₁= 2 х.. Отсюда можно получить несколько первых многочленов Эрмита:

H ₂(x) = 4 x ² - 2,

H ₃(x) = 8 x ³ - 12 x,

H₄ (x) = 16 х ⁴ - 48 x ² + 12. и т.д.

Дата добавления: 2014-01-04