Безмоментное НДС сферической оболочки резервуара

Методика расчета на прочность шаровых резервуаров

Сферическая оболочка резервуаров опирается либо на цилиндри­ческий поста­мент, диаметр которого равен радиусу резервуара, либо на систему опорных стоек, связанных между собой упругими связями. Число опорных стоек в за­висимости от вместимости резерву­ара колеблется от 8 до 16 и принимается кратным числу лепесков по кругу опирания. В нижней части стойки приварена плита, через которую она опирается на кольцевой фундамент и крепится ан­керными болтами. Верх стойки имеет вырез по радиусу шара и крепится с по­мощью электросварки через фасонную штампованную пластину к оболочке резервуара.

Упругая связь оболочки с опорными стойками благоприятно ска­зывается на работе конструкции, так как оболочка имеет возможно­сть за счёт упругой по­датливости стоек деформироваться в радиаль­ном направлении при действии эксплуатационной нагрузки. Вот по­чему в настоящее время это конструктив­ное решение прочно вошло в практику зарубежного и отечественного резер­вуаростроения.

Для определения НДС сферической оболо­чки резервуара, опёртой на ряд равностоящих стоек при действии эксплуатационной нагрузки, будем придер­живаться следующего алгоритма. Сначала рассчитаем оболочку резервуара по безмоментной теории, затем определим краевые эффекты в области её сопря­жения с опорными стойками и, складывая полученные решения, получим пол­ное НДС шарового резервуара.

Для решения поставленной задачи воспользуемся уравнениями равновесия бесконечно-малого элемента (рис.11.13), выделенного из сферической оболочки, при действии произвольной нагрузки, удовлетворяющей условиям существования безмоментного напряженного состояния.

Рис.11.13. Положительные направления усилий и перемещений в сфериче­ской оболочке при безмоментном решении

Исключим из этих уравнений кольцевое усилие N₂

(11.63)

Введем в уравнения (11.63) новые переменные, обозначив:

(11.64)

Тогда уравнения (11.63) примут следующий вид:

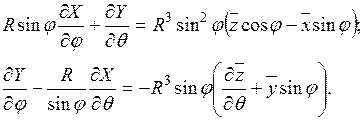(11.65)

Исключим из системы уравнений (11.65) Y:

(11.66)

Дифференциальное уравнение (11.66) содержит две независимые переменные j и q, что усложняет его интегрирование. Но так как сферическая обо­лочка замкнута в окружном направлении, то компоненты поверхностной нагрузки , , , а также все факторы НДС оболочки можно представить в виде периоди­ческих функций угла q (с периодом 2p).

После подстановки этих функций дифференциальное уравнение (11.66) в ча­ст­ных производных становится обыкновенным дифференциальным уравне­ни­ем относительно независимой переменной j, решение которого значительно упрощается.

Итак, представим компоненты поверхностной нагрузки в форме (10.22), а все факторы безмоментного НДС оболочки шарового резервуара в соответствии с периодическим характером нагрузки – в форме (10.23). Тогда и решение диф­ференциального уравнения (11.65) можно записать в следующем виде:

(11.67)

После подстановки (10.22) и (11.67) в (11.66) получим:

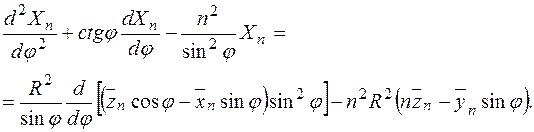(11.68)

В нашем случае шаровая оболочка резервуара опирается по экватору на i опорных стоек (рис.2.16), расположенных друг от друга на расстоянии 2pR/i. Опорная конструкция оголовка стойки приварена к фасонной пластине, имею­щей кривизну 1/R в меридиональном и экваториальном направлениях и шири­ну Rq₀, так что опорная пластина контактирует по всей своей поверхности с наружной поверхностью сферической оболочки.

При эксплуатации сферического резервуара его оболочка испытывает одно­временное воздействие гидростатического давления хранимой жидкости уде­ль­ного веса g, избыточного давления газа p и сжимающей краевой нагрузки со стороны опорных стоек. Рассчитаем оболочку сферического резервуара на дей­ствие этих нагрузок.

В данном случае компоненты поверхностной нагрузки равны:

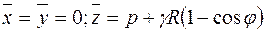(11.69)

и ввиду симметрии действия нагрузок n = 0, S = 0, v = 0, Y = 0.

Поэтому из первого уравнения системы (11.64) следует:

Откуда

Так как оболочка шарового резервуара замкнута в вершине, то j₁ = 0, С₁ = 0 и поэтому с учетом (11.69) получим:

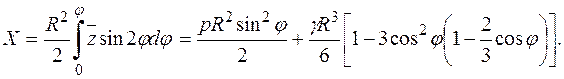(5.70)

Теперь с помощью зависимости (11.64) можно определить выражение мери­дионального усилия для области оболочки, расположенной выше опорного се­чения, т.е. при a = :

(11.71)

Выражение для кольцевого усилия определяется из третьего условия равно­весия бесконечно-малого элемента оболочки (3.22):

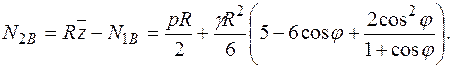(11.72)

Согласно второму уравнению (10.23) горизонтальное перемещение средин­ной поверхности оболочки резервуара определяется как

(11.73)

Угол поворота касательной к меридиану оболочки резервуара можно вычис­лить с помощью следующей зависимости:

(11.74)

Для определения внутренних усилий и.перемещений в нижней области обо­лочки (j > a) необходимо помимо внутреннего давле­ния в резервуаре учиты­вать сумму вертикальных реакций со стороны опорных стоек. Эта сумма скла­дывается из полного веса жидкости хранимой в оболочке и её собственноговеса: 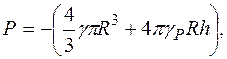(11.75)

где g_Р, - удельный вес материала оболочки резервуара.

Несмотря на то, что гидростатическое давление хранимой жидкости и из­быто­чное давление газа оказывают симметричное воздействие на оболочку ре­зервуара относительно вертикальной оси, все факторы её НДС являются функ­циями двух переменных j и q, так как в опорном сечении у экватора при j =a = p/2 краевая нагрузка распределе­на неравномерно в окружном направлении.

Если предположить, что на каждой опоре давление со стороны резервуара распределено равномерно, то эпюра меридионального уси­лия у экватора (краевая нагрузка) будет иметь вид, представленный на рис.11.14, а сжимающее усилие на опоре равно: (11.76)

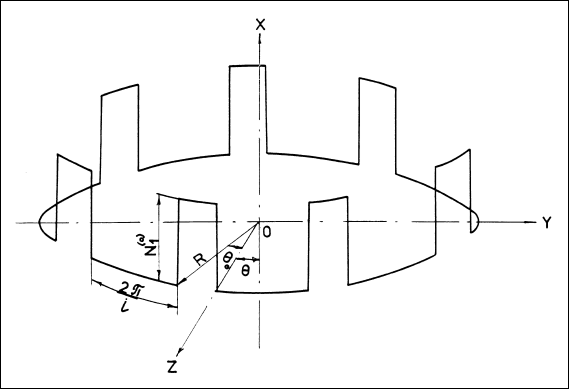
Рис.11.14. Краевая нагрузка со стороны опорных стоек на оболочку резер­вуара у экватора

Аппроксимируем эту ступенчатую краевую нагрузку рядом Фурье при j = a = p/2.

(11.77)

Выражение для меридионального усилия в произвольной точке нижней по­лусферы при p ³ j > p/2 можно представить в виде суммы безмоментного ре­шения для резервуара, покоящегося на сплошной опоре и краевого решения однородного уравнения (11.67)

(11.78)

Краевое усилие N_1n для n-го члена разложения в ряд Фурье опре­делим путём решения уравнения (11.67), которое при 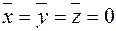запишется:

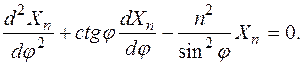(11.79)

Его общим решением будет 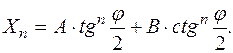(11.80)

При определении постоянных интегрирования А и В необходимо прежде всего учесть то, что нижняя полусфера резервуара замкнута в ниж­ней точке при j = p. Поэтому следует исключить ту часть из ре­шения (11.80), которая при j = p обращается в бесконечность. Следовательно А = 0 и выражение для ме­ридионального краевого усилия с учётом (11.64) примет вид:

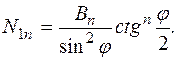(11.81)

После подстановки N_1n в (11.78 ) получим:

(11.82)

Произвольные постоянные для n-го члена разложения в ряд Фурье найдем, приравнивая коэффициенты этого ряда соответствующим коэффициентам ряда (11.77).

(11.83)

Тогда после подстановки (11.75) в (11.83), а полученное значение B_n - в (11.82), окончательно будем иметь следующее выражение для определения меридио­нального усилия в нижней области оболочки шарового резервуара:

(11.84)

где 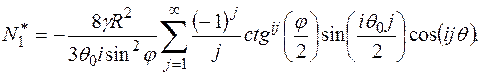(11.85)

Выражение для кольцевого усилия в нижней полусфере резервуара опреде­лится из условия равновесия бесконечно-малого элемента оболочки

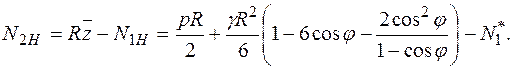(11.86)

Сдвигающее усилие можно найти из совместного решения уравнений (11.64) и (11.65) с учетом (11.69)

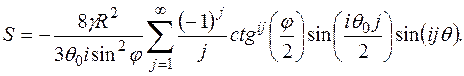(11.87)

Тогда горизонтальное перемещение срединной поверхности оболочки ниж­ней полусферы и угол поворота касательной к меридиану будут соответствен­но равны:

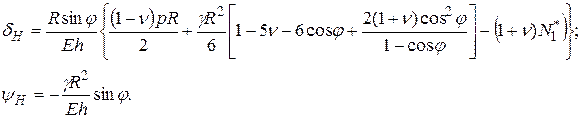(11.88)

Сходимость рядов (11.85) и (11.87) существенно зависит от величины ,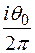

т.е. от отношения ширины опорной части стойки к расстоянию между ними. Чем меньше это отношение, тем хуже сходимость ряда. Например, при 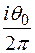= 0,25 для получения достаточно точного резу­льтата необходимо удержать в ря­дах (11.85) и (11.87) 15 членов, а при 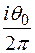= 0,044 - шестьдесят членов.

Чтобы иметь представление о поведении функции меридионально­го крае­вого сжимающего усилия 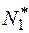в меридиональном и экваториаль­ном направле­ниях сферической оболочки резервуара проведём её численный анализ. Прак­тически угол раствора опорной пластины сто­йки может меняться в пределах от 2° до 8°. Число опорных стоек i зависит от вместимости резервуара.

Таблица 11.1

Вместимость резервуара, м ^3;
Число стоек, i

Задаваясь последовательно в формуле (11.85) q₀ = 2°, 4°, 6°, 8° и i = 8, 12, 16,

можно получить графические зависимости и . Так как для нормальной сходимости ряда Фурье следует удерживать в нём от 15 до 60 чле­нов, численный анализ функции 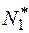целесообразно проводить на ЭЦВМ. Графические зависимости функций и представлены на рис.11.15 – 11.17.

Из анализа этих зависимостей для произвольных значений i и q₀ следует, что величина меридионального краевого усилия, действующего в экваториальном сечении (j = p/2) сфери­ческой оболочки, в области между опорными стойками постоянна и равна: (11.89)

Сжимающее краевое меридиональное усилие быстро затухает в меридио­нальном направлении при уда­лении от опоры. О степени затухания этого усилия в окружном и меридиональном направ­лениях оболочки можно судить по рис.11.15 – 11.17.

Таким образом, в сечении j = a = p/2 сферической оболочки резервуара, расположенном между опорами, функции внут­ренних усилий и перемещений равны:

(11.90)

То-есть сферическая оболочка резервуара, расположенная вне опорных се­чений, находится в безмоментном НДС.

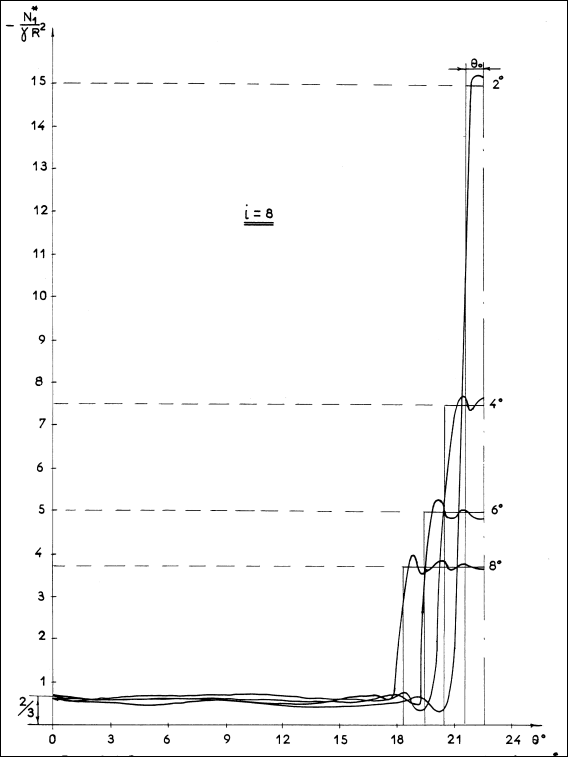
Рис.11.15.Эпюры краевых меридиональных усилий в окружном направлении у экватора при j = p/2; i = 8; j = 60;q₀ = 2⁰, 4⁰, 6⁰, 8⁰

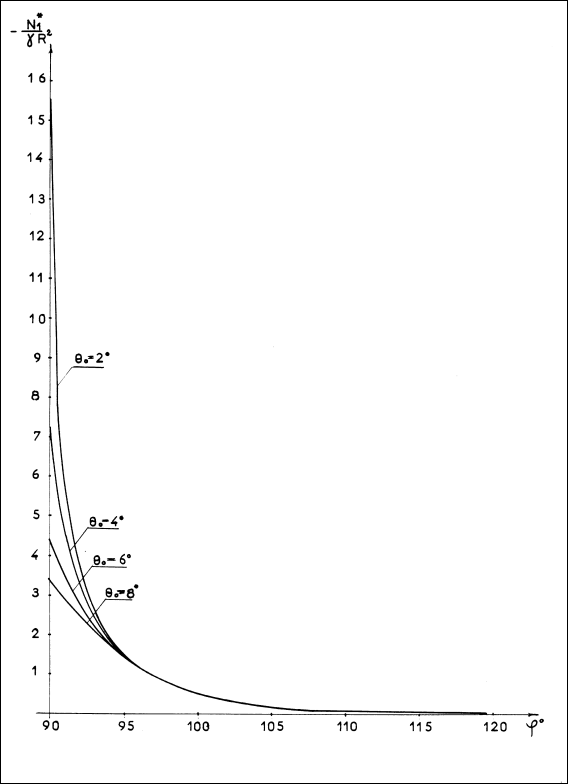
Рис.11.16. Эпюры краевых меридиональных усилий в сечениях оболочки, совпадающих с осью опорных стоек

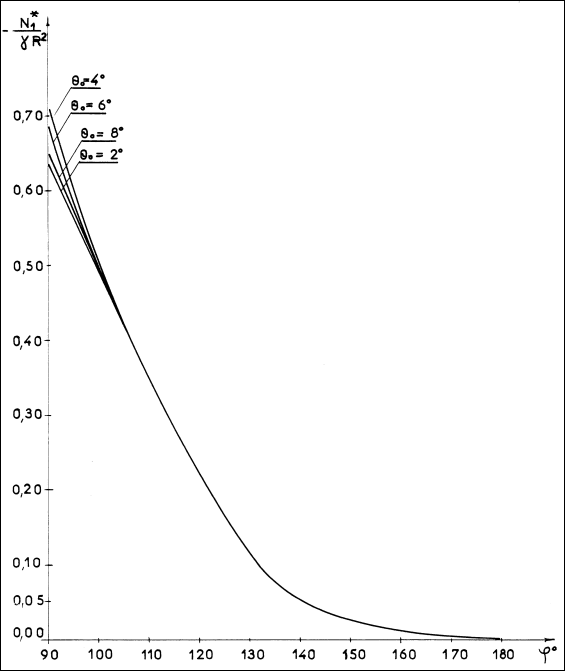
Рис.11.17. Эпюры краевых меридиональных усилий в зонах оболочки, расположенных между опорами

Эпюры напряжений и радиальных перемещений для безмоментной области сфе­рической оболочки в безразмерном виде

,

построенные с помощью формул (11.71) – (11.73) и (11.84), (11.86), (11.88) при p = 0, представлены на рис.11.18.

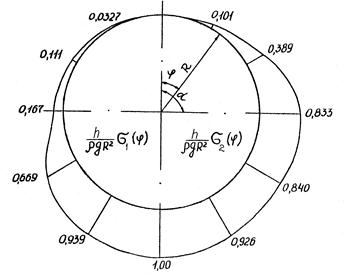
Рис.11.18.Эпюры напряжений и радиального перемещения в безмоментной области оболочки резервуара

Что касается меридиональных сечений, проходящих через опорную часть стоек, то здесь наблюдается разрыв непрерывности в функциях безмоментных внутренних усилий и перемещений, что неизбежно приво­дит к изгибу.

Определим напряженно-деформированное состояние сферической оболочки резервуара в местах её опирания на оголовки вертикальных трубчатых стоек, связанных между собой диагональными упругими связями с натяжными при­способлениями (талрепами).

Дата добавления: 2014-01-04