Свойства потенциальных полей

Потенциальные и соленоидальные векторные поля.

Определение 1:

Векторное поле 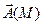называется потенциальным, если оно является градиентом некоторого скалярного поля :

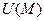При этом функция 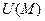называется потенциалом векторного поля .

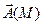- циркуляция равна нулю по " замкнутому контуру .

Действительно,

Если векторное поле 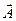задано в односвязной области D, то для его потенциальности необходимо и достаточно, чтобы его .

Таким образом, потенциальное поле является “безвихревым”.

Односвязная область – такая область, граница которой может быть стянута в точку непрерывным образом, не выходя за пределы области.

Доказательство:

Рис. 25.5.Односвязная

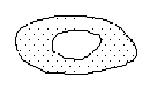
Рис. 25.6. Не является односвязной

Необходимость:

Если векторное поле 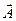потенциально, т.е. , то его .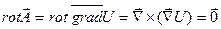

Достаточность:

Если 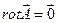, то все компоненты этого вектора равны 0, т.е.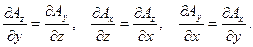

Переобозначив получим: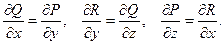

В этих равенствах легко узнать необходимые и достаточные условия для того, чтобы выражение 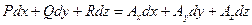было полным дифференциалом функции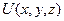 т.е. поле 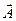является потенциальным, что и требовалось доказать.

Если вспомнить доказательство достаточных условий полного дифференциала (в двумерном случае – с помощью формулы Грина), то становится понятно, что эти условия (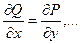) должны выполняться во всех точках некоторой области, которая рассматривалась как односвязная область.

Можно показать, что в случае области, которая не является односвязной, этих условий может оказаться недостаточно для восстановления однозначной функции 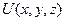во всей области.

Потенциал потенциального поля 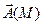определяется с точностью до постоянного слагаемого.

Действительно,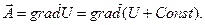

Если векторное поле 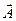потенциально, то его работа между двумя точками пространства не зависит от формы пути, по которому соединяются эти точки, и равна разности значений потенциала в этих точках.

Доказательство:

т.е. работа равна разности значений потенциала и не зависит от формы перемещения .

Найти потенциал векторного поля 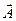можно, например, с помощью криволинейного интеграла II рода от фиксированной точки 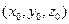до переменной точки :

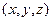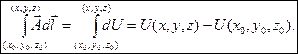
При этом удобно вычислять криволинейный интеграл, как независящий от формы линии интегрирования, по ломаной, состоящей из отрезков, параллельных осям координат. Точки 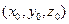, 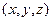и линия интегрирования должны оставаться в области существования этого криволинейного интеграла.

Пример:

Убедиться в том, что векторное поле потенциально, и найти его потенциал:

Решение.

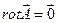- это необходимое и достаточное условие потенциальности поля. Вычисляем:

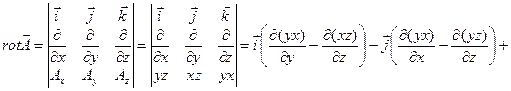
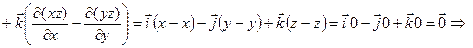поле является потенциальным.

Рис. 25.7.

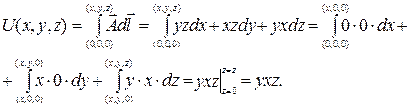
Ответ:

Определение 2:

Векторное поле 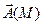называется соленоидальным в односвязной области D, если в любой точке этой области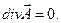

Дата добавления: 2014-01-04