Колебания упругих систем под действием подвижной нагрузки

Лекция 26, 27

Поводом для постановки первых теоретических и экспериментальных исследований динамического действия подвижных нагрузок послужило обрушение Честерского моста (Англия) в 1847 г.

Первая попытка теоретического решения – Кокс (1848) для задачи

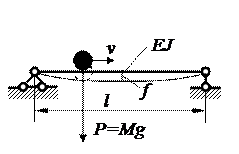
Динамический коэффициент для этой задачи по Коксу .

Рассуждения Кокса следующие: работа силы, когда груз находится в середине пролета.

Потенциальная работа упругой деформации балки

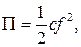где

Действительно, податливость (единичное перемещение точки приложения единичной силы)

Тогда потенциальная энергия определится как

Закон сохранения энергии дает

Уже через год Стокс опроверг этот результат: Баланс энергии у Кокса не учитывает работу горизонтальной силы, необходимой для поддержания скорости груза постоянной.

Дальнейшие исследования – различные постановки задачи

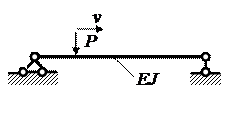
		Балка и груз - безинерционные
		Груз – инерционный, балка - безинерционная
		Балка – инерционная, груз - безинерционный
		Балка и груз – инерционная

Некоторые другие задачи на действие подвижной нагрузки

а)
б)
в)
г)	M v
д)
е)
ж)

Рассмотрим простейшие задачи

1. Схема 1. Действие безинерционной подвижной нагрузки на безинерционную балку (схема 1). Винклер, Мор (середина XIX века). Динамики нет, только кинематика.

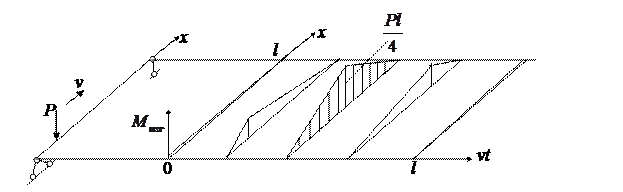
Строится линия влияния. Такое приближение справедливо для малых скоростей движения .

2. Схема 2 (инерционный груз, безинерционная балка). Исследование сводится к решению задачи о массе на пружине с переменной во времени жесткостью (Виллис – 1849).

Уравнение движения

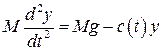
Координата массы является функцией времени

Уравнение движения можно переписать

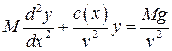
Определим жесткость балки как функцию координаты массы

Используя метод Максвелла-Мора, получим

Окончательно уравнение движения массы имеет вид

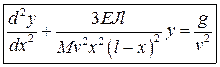
Это дифференциальное уравнение с переменными коэффициентами. Решение Стокса (приближенное в рядах и в квадратурах). Коэффициент динамичности в первом приближении

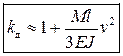
Буссинеск (1883) – предложил замену переменных

,

которая приводит к уравнению с постоянными коэффициентами

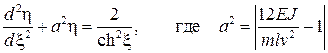
Ошибка Бресса (1859)

Пусть , т.е. груз находится посередине пролета балки. Изгибающий момент в этом сечении равен

(*)

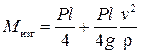Здесь 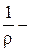кривизна траектории движения груза,

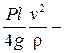дополнительный изгибающий момент от центробежной силы.

Из элементарной теории изгиба стержней имеем

(**)

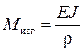Исключая 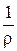из соотношений (*) и (**), получим

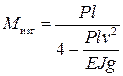
Отсюда получаем критическое значение скорости движения груза

,

при котором изгибающий момент стремится к бесконечности .

Но это решение неверно, т.к. 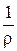в выражении (*) и 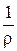в выражении (**) разные: соответственно – кривизна траектории и кривизна упругой линии. Это разные величины

т. 1, 2, 3, 4 – различные моменты времени через интервал

Указанные кривизны различны и для схемы 1.

3. Схема 3. Безинерционная нагрузка, инерционная балка

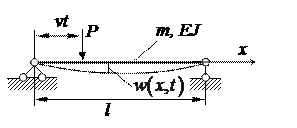
На балку действует подвижная сосредоточенная сила, которую представим с помощью дельта-функции и учтем в уравнении движения внешнее трение 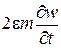. Тогда получим

.

Это уравнение интегрируется с нулевыми начальными условиями. Применим метод собственных функций (метод разложения по формам собственных колебаний)

Подставим в уравнение, умножим на 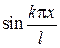и проинтегрируем от 0 до 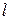(процедура метода Бубнова-Галеркина)

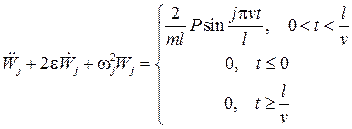
Для отрезка времени имеем задачу о вынужденных колебаниях. С помощью интеграла Дюамеля

Далее решается задача о свободных колебаниях с начальными условиями при .

Через обозначено

Для усилий ряды оказываются расходящимися, но для ряд сходится. Хуже ряд сходится для напряжений.

Введем параметры

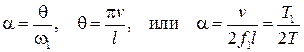
Здесь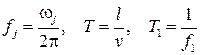

Для получим следующую формулу

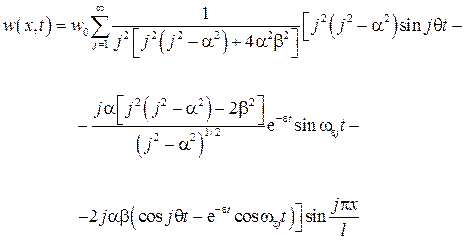
где

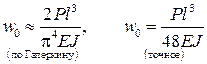
В случае отсутствия диссипации

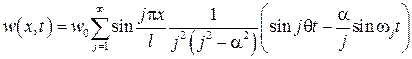
При могут быть особенности

Некоторые графики

Для стальной балки , т.е. для реальных конструкций критические скорости не достигаются.

4. Схема 4. Груз и балка – инерционные.

Для определения сил инерции груза необходимо учитывать, что его координата зависит от времени, т.е. 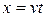. Поэтому проекция скорости груза на ось равна полной производной по времени

Обычно ищут решение без второго члена, соответствующего кариолисову ускорению для схем

Применяют метод собственных функций

,

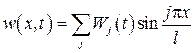однако система уравнений относительно обобщенных координат не разделяется

В некоторых задачах второй член является главным (задачи динамической неустойчивости). Задача в этом случае оказывается неконсервативной.

А.П.Филиппов предложил сводить к интегральному уравнению с последующим численным решением

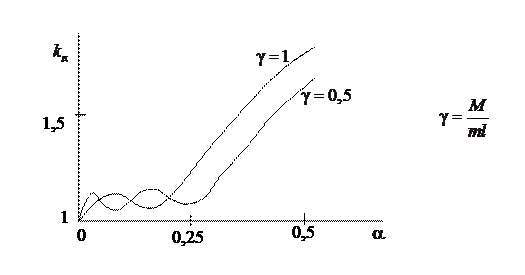
Дата добавления: 2014-01-04