Пример 2

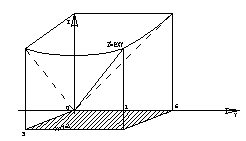
Найти двойным интегрированием объем тела, ограниченного поверхностями: параболоидом вращения 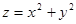, координатами плоскостями и плоскостью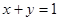

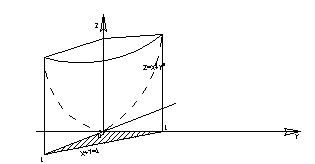
Решение:

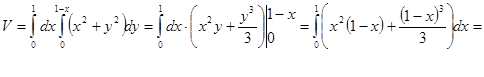
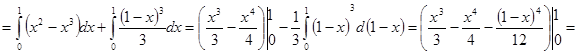
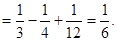
3.(Площадь поверхности)

Пусть область 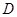есть проекция куска поверхности 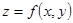на плоскость 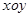. Тогда площадь куска поверхности 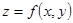определяется по формуле:

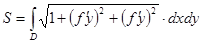
Пример 3

Вычислить площадь той части поверхности 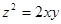, которая находится над прямоугольником, лежащим в плоскости и ограниченным прямыми , , , .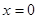

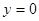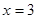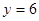Решение: (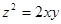- коническая поверхность с вершиной в начале координат и осью симметрии )

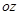1)

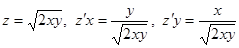
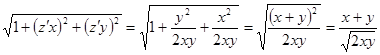
2)

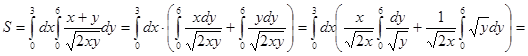
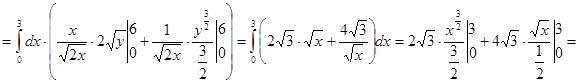
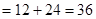
Тройной интеграл.

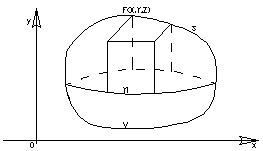
Пусть в пространстве задана некоторая область , ограниченная замкнутой поверхностью 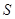. Пусть в области и на ее границе определена некоторая непрерывная функция .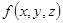

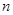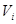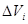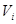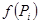Разобьем область произвольным образом на области , обозначая через ее объем. В пределах каждой частной области выберем произвольную точку и обозначим через значения функции 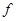в этой точке.

Поставим интегральную сумму вида (1)

и будем неограниченно увеличивать число малых областей 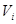так, чтобы наибольший диаметр 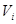стремился к 0. Если функция 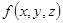непрерывна, то при этом будет существовать предел сумм (1). Этот предел, не зависящий ни от способа разбиения , ни от выбора точек , обозначается:

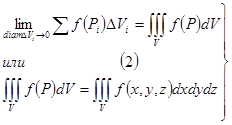тройной интеграл

Если 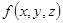считать объемной плоскостью распределения вещества в области , то интеграл (2) дает массу всего вещества, заключенного в объеме .

Сведение тройного интеграла к трехкратному.

Предположим, что область , ограниченная замкнутой поверхностью 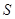, обладает следующими свойствами:

1) всякая прямая, параллельная оси 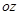, проведенная через внутреннюю точку области , пересекает поверхность 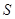в двух точках;

2) вся область проектируется на плоскость 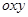в правильную область ;

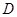3) всякая часть области , отсеченная плоскостью, параллельной оной из координатных плоскостей , также обладает свойствами 1) и 2).

Область , обладающая указанными свойствами находятся правильной трехмерной областью (эллипсоид, тетраэдр, прямоугольный параллелепипед и т. д.).

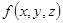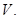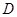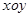Пусть функция определена и непрерывна в области Пусть область - проекция на плоскость . Тогда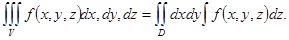

Чтобы найти пределы внутреннего интеграла, перенесем область прямой, параллельной оси :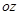

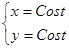
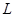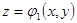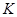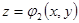Точка входа этой прямой в область имеет аппликату , точка выхода из области имеет аппликату . Тогда

Представив 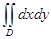в виде двукратного интеграла, получим формулы:

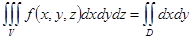в виде двукратного интеграла, получим формулы:

.

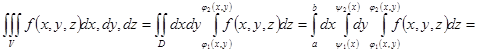
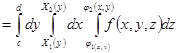Вычисление трехкратного интеграла начинают с внутреннего (по 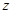, считая 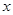и 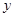- постоянными) интеграла,

затем переходят к среднему и наконец, к внешнему интегралу.

Замечания:

а) Пусть область 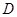есть проекция области на плоскость 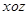. Тогда

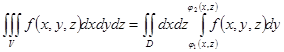, где 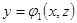, 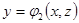есть соотвественно ординаты точек входа и выхода прямой, пересекающей область и параллельной оси .

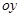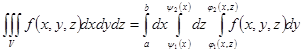или .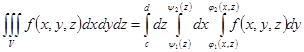

б) Если наиболее очевидна проекция области на плоскость , то тройной интеграл следует представить в виде:

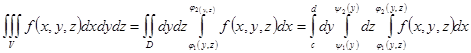и далее найти пределы трехкратного интеграла указанными способами.

Дата добавления: 2014-01-04