Лекция 29

Эволюционная теория биологических ритмов.

Ритмичность первоначально возникает в результате периодического воздействия окружающей среды, затем закрепляются генетически. В настоящее время ритмы генерируются внутренним механизмом, но период их синхронизируется с частотой внешних стимулов.

Из биоритмологии выделились:

- хронобиология;

- хронопатология;

- хронодиагностика;

- хронотерапия;

- хронофармакология (прием препаратов в определенное время);

- хроногигиена (соблюдение режима труда отдыха).

Ряды Фурье по ортогональным системам

Пусть в бесконечномерном пространстве Е со скалярным произведением дана ортогональная система (j_k), т.е. j_k ¹ 0, k=1,2,…; (j_k, j_l)=0 при l ¹ k. Ряд вида называется рядом по ортогональной системе (j_k). Пусть хÎЕ. Числа коэффициентами Фурье элемента х по ортогональной системе (j_k), а ряд называется рядом Фурье (по ортогональной системе (j_k)), составленным для элемента х (ряд элемента х). Многочлен 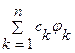- частичная сумма ряда Фурье – называется многочленом Фурье (элемента х).

Возьмем теперь первые n векторов ортогональной системы (j_k): j₁, j₂,…, j_n. Образуем всевозможные их линейные комбинации вида . В результате мы получаем n-мерное подпространство L_n в Е. Иногда говорят, что L_n натянуто на j₁, j₂,…, j_n, или что L_n является линейной оболочкой на j₁, j₂,…, j_n. Возьмем теперь элемент хÎЕ и вычислим квадрат расстояния между х и u_n: .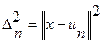

Рассуждения ведутся для случая комплексного Е. В вещественном случае вся выкладки тоже справедливы, но несколько упрощаются. Пользуясь свойствами скалярного произведения, получаем 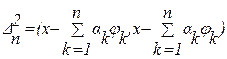= (х,х) - .

Заметим теперь, что (х, j_k)=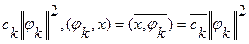, где с_k – коэффициент Фурье элемента х.

Следовательно .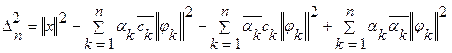

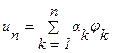Далее, , и мы получаем . Теперь мы можем вычислить d_n=r(x,L_n) = , где D_n – зависит от , т.е. от n комплексных переменных a₁, a₂,…, a_n. Явная формула, полученная для 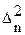, показывает, что d_n достигается при a_k = c_k, k=1,2,…,n. Это свойство коэффициентов с₁, с₂,…, с_n называется экстремальным свойством коэффициентов Фурье. Итак, доказана следующая

Теорема 29.1. Пусть (j_k) ортогональная в пространстве со скалярным произведением Е, пусть L_n – подпространство натянутое на j₁, j₂,…, j_n. Тогда d_n=r(x,L_n), хÎЕ, дается следующими формулами: 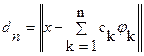, , 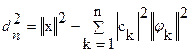где c_k, k=1,2,…,n – коэффициенты Фурье элемента х по системе (j_k).

Следствие. Если m>n, то . Действительно, по формуле .

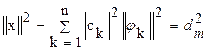Осталось воспользоваться формулой .

Итак, наилучшее приближение элемента х посредством элементов из L_n есть многочлен Фурье элемента х: .

Так как , то из формулы 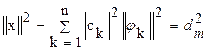следует .

Слева стоит частичная сумма числового ряда 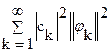с неотрицательными членами, причем оценка верна для любого n.

Ряд с неотрицательными членами сходится тогда и только тогда, когда последовательность его частичных сумм ограничена. Следовательно, из вытекает сходимость ряда 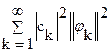и неравенство для его суммы . (4)

Это неравенство называется неравенством Бесселя. Его справедливость доказана для любой ортогональной системы в любом бесконечном пространстве со скалярным произведением.

Следствие. Если то коэффициенты Фурье с_к любого элемента хÎЕ стремятся к нулю при k®¥.

Равенство Парсеваля – Стеклова

ОПРЕДЕЛЕНИЕ 29.1. Ортогональная система (j_k) из гильбертова пространства Н называется полной, если для любого хÎН (ряд Фурье, составленный для х, сходится к х).

Полная ортогональная система называется ортогональным базисом гильбертова пространства Н.

Из предыдущего имеем . Отсюда приходим к заключению: для того чтобы система (j_k) была полной, необходимо и достаточно, чтобы .

Таким образом, в случае полной системы и только в этом случае неравенство Бесселя превращается в равенство. Это равенство называется равенством Парсеваля-Стеклова. Заметим, что полнота ортогональной системы означает, что ее нельзя дополнить до более широкой ортогональной системы путем присоединения новых элементов.

ОПРЕДЕЛЕНИЕ 29.2. Ортогональная нормированная система (j_k) называется замкнутой, если для любого хÎЕ справедливо равенство .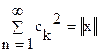

Замкнутость системы (j_k) равносильна тому, что для каждого fÎН частичные суммы ряда Фурье сходятся к f.

Понятие замкнутости ортогональной нормированной системы тесно связано с понятием полноты системы.

Теорема 29.2. В сепарабельном евклидовом пространстве Е всякая полная ортогональная нормированная система является замкнутой и обратно.

Доказательство. Пусть система (j_k) замкнута, тогда каков бы ни был элемент хÎЕ, последовательность частичных сумм его ряда Фурье сходится к f. Это означает, что линейные комбинации элементов системы (j_n) полны в Е, т.е. система (j_n) полна. Обратно, пусть система (j_n) полна, т.е. любой элемент хÎЕ можно сколь угодно точно аппроксимировать линейной комбинацией элементов системы (j_k); частичная сумма 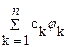ряда Фурье для х дает не менее точную аппроксимацию.

Следовательно, ряд 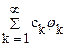сходится к х, и равенство Парсеваля-Стеклова имеет место.

Пример29.1.

В гильбертовом пространстве L² [-p;p] функций суммируемых с квадратом модуля на отрезке [-p;p] функции 1, cos t, sin t, sin 2t,… образуют ортогональный базис. Однако эта система функций не является нормированной.

Пример29.2.

Пусть векторы х и у ортогональны, тогда по аналогии с элементарной геометрией вектор х+у можно назвать гипотенузой прямоугольного треугольника, построенного на векторах х и у. Умножая х+у скалярно на себя и используя ортогональность векторов х и у, мы получаем .

Мы доказали тем самым в общем гильбертовом пространстве теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Нетрудно обобщить эту теорему на случай любого конечного числа слагаемых. Именно пусть векторы х₁, х₂, …, х_k взаимно ортогональны и z= х₁+ х₂+ …+ х_k, тогда .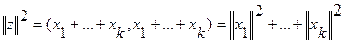

Дата добавления: 2014-01-04