Формула Грина

Установим связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом по границе L этой области.

Пусть в плоскости О ху дана ограниченная замкнутым контуром L правильная область D. Кривые, ограничивающие эту область снизу и сверху, заданы уравнениями

y = y₁(x) и y = y₂(x), y₁(x) ≤ y₂(x), a ≤ x ≤ b (рис.1).

y

P

y=y₂(x)

M D N

y=y₁(x)

Q

O a b x

Рис. 1.

Зададим в области D непрерывные функции P(x, y) и Q(x, y), имеющие непрерывные частные производные, и рассмотрим интеграл

.

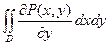Переходя к двукратному интегралу, получим:

(26.5)

Так как у = у₂(х) – параметрическое выражение кривой МPN, то

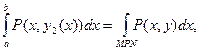
где справа стоит криволинейный интеграл по кривой MPN. Аналогично получаем, что

.

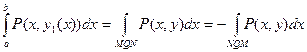Подставим полученные результаты в формулу (26.5):

(26.6)

так как контур L представляет собой объединение кривых MPN и NQM.

Так же можно получить, что 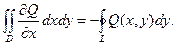(26.7)

Вычтем из равенства (26.6) равенство (26.7):

При этом обход контура L происходит по часовой стрелке. Изменим направление обхода. Тогда предыдущее равенство примет вид:

(26.8)

Эта формула, задающая связь между двойным интегралом и криволинейным интегралом 2-го рода, называется формулой Грина.

Замечание 1. Если в криволинейном интеграле по замкнутому контуру не указано направление обхода, то предполагается, что он производится против часовой стрелки.

Замечание 2. Если рассматривать в плоскости О ху векторное поле { P(x,y), Q(x,y) }, то в правой части формулы (26.8) стоит его циркуляция по контуру L.

Пример. Вычислим циркуляцию векторного поля { x + sin x, х – e^у } по контуру x ²+ y ²=1.

Применим формулу Грина, учитывая, что :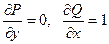

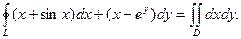Область D при этом – круг единичного радиуса с центром в начале координат. Перейдем к полярным координатам:

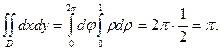
Практическое применение криволинейных интегралов

Дата добавления: 2014-01-04